数学专栏课外加餐（一） 我们为什么需要反码和补码？ 你好，我是黄申。欢迎来到第一次课外加餐时间。

专栏已经更新了几讲，看到这么多人在留言区写下自己的疑惑和观点，我非常开心。很多同学在留言里提出了很多非常好的问题，所以我决定每隔一段时间，对留言里的疑问、有代表性的问题做个集中的解答，也是对我们主线内容做一个补充，希望对你有帮助。

什么是符号位？为什么要有符号位？

在第1讲里，我介绍了十进制数转二进制数。这里面很多人对逻辑右移和算术右移中提到的符号位和补码有疑惑。这里面涉及了几个重要的概念，包括符号位、溢出、原码、反码和补码。我详细讲一下这几个点的来龙去脉。

首先我们来看，什么是符号位，为什么要有符号位？用一句话来概括就是，符号位是有符号二进制数中的最高位，我们需要它来表示负数。

在实际的硬件系统中，计算机CPU的运算器只实现了加法器，而没有实现减法器。那么计算机如何做减法呢？我们可以通过加上一个负数来达到这个目的。比如，3-2可以看作3+(-2)。因此，负数的表示对于计算机中的二进制减法至关重要。

那么，接下来的问题就是，如何让计算机理解哪些是正数，哪些是负数呢？为此，人们把二进制数分为有符号数（signed）和无符号数（unsigned）。

如果是有符号数，那么最高位就是符号位。当符号位为0时，表示该数值为正数；当符号位为1时，表示该数值为负数。例如一个8位的有符号位二进制数10100010，最高位是1，这就表示它是一个负数。

如果是无符号数，那么最高位就不是符号位，而是二进制数字的一部分，例如一个8位的无符号位二进制数10100010，我们可以通过第1讲讲过的内容，换算出它所对应的十进制数是162。由于没有表示负数的符号位，所有无符号位的二进制都代表正数。

有些编程语言，比如Java，它所有和数字相关的数据类型都是有符号位的；而有些编程语言，比如C语言，它有诸如unsigned int这种无符号位的数据类型。

下面我们来看，什么是溢出？

在数学的理论中，数字可以有无穷大，也有无穷小。可是，现实中的计算机系统，总有一个物理上的极限（比如说晶体管的大小和数量），因此不可能表示无穷大或者无穷小的数字。对计算机而言，无论是何种数据类型，都有一个上限和下限。

在Java中，int型是32位，它的最大值也就是上限是2^31-1（最高位是符号位，所以是2的31次方而不是32次方），最小值也就是下限是-2^31。而long型是64位，它的最大值，也就是上限是2^63-1；最小值，也就是下限是-2^63。

对于n位的数字类型，符号位是1，后面n-1位全是0，我们把这种情形表示为-2^(n-1) ，而不是2^(n-1)。一旦某个数字超过了这些限定，就会发生溢出。如果超出上限，就叫上溢出（overflow）。如果超出了下限，就叫下溢出（underflow）。

那么溢出之后会发生什么呢？我以上溢出为例来给你解释。

n位数字的最大的正值，其符号位为0，剩下的n-1位都为1，再增大一个就变为了符号位为1，剩下的n-1位都为0。而符号位是1，后面n-1位全是0，我们已经说过这表示-2^(n-1)。

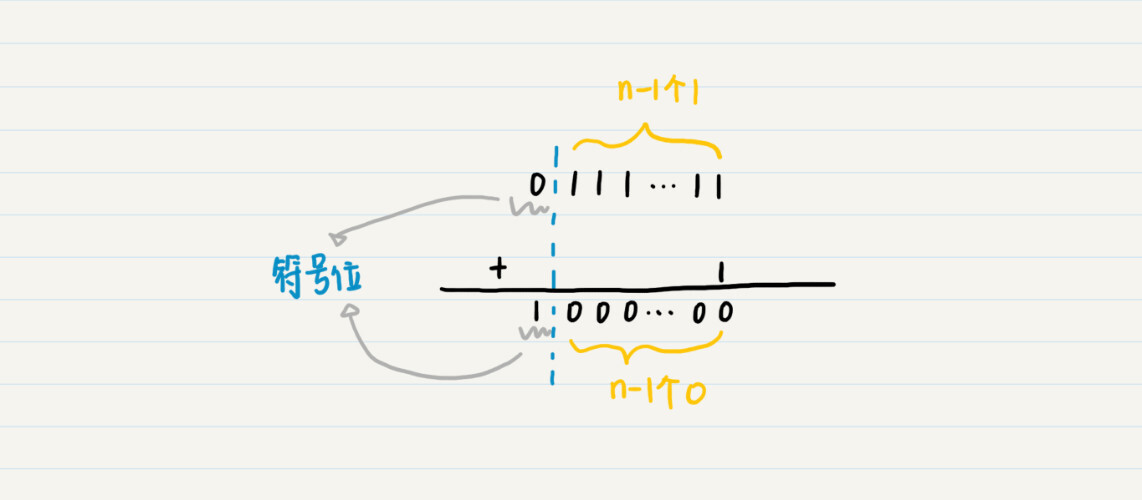
那么就是说，上溢出之后，又从下限开始，最大的数值加1，就变成了最小的数值，周而复始，这不就是余数和取模的概念吗？下面这个图可以帮助你理解。

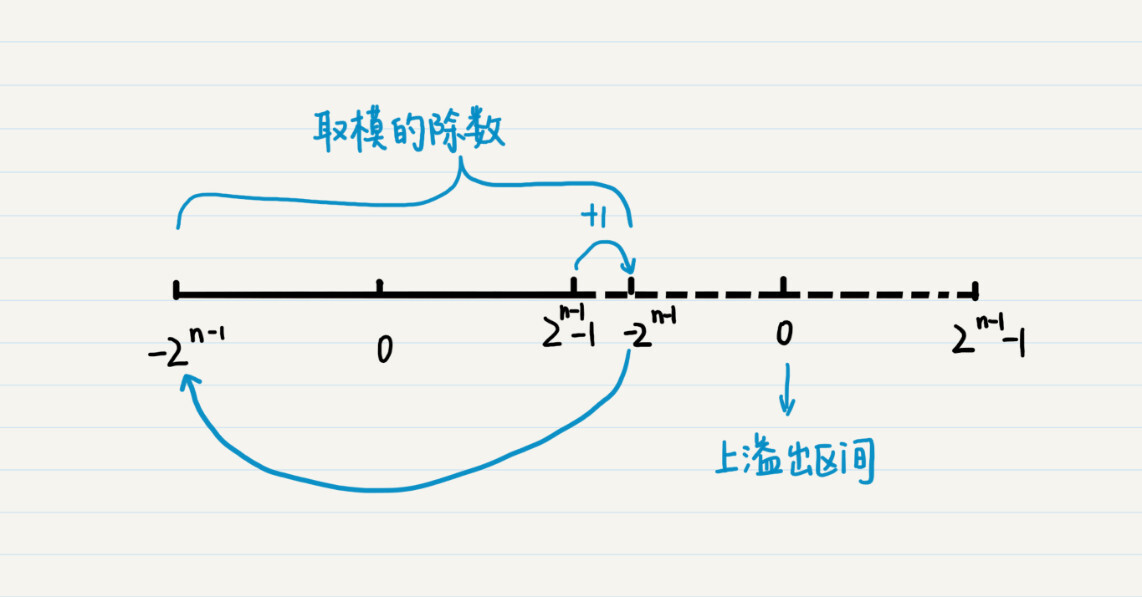
其中右半部分的虚线表示已经溢出的区间，而为了方便你理解，我将溢出后所对应的数字也标在了虚线的区间里。由此可以看到，所以说，计算机数据的溢出，就相当于取模。而用于取模的除数就是数据类型的上限减去下限的值，再加上1，也就是(2^(n-1)-1)-(-2^(n-1))+1=2x2^(n-1)-1+1=2^n-1+1。

你可能会好奇，这个除数为什么不直接写成2^n呢？这是因为2^n已经是n+1位了，已经超出了n位所能表示的范围。

二进制的原码、反码及补码

理解了符号位和溢出，我接下来说说，什么是二进制的原码、反码和补码，以及我们为什么需要它们。

原码就是我们看到的二进制的原始表示。对于有符号的二进制来说，原码的最高位是符号位，而其余的位用来表示该数字绝对值的二进制。所以+2的原码是000…010，-2的的原码是100.…010。

那么我们是不是可以直接使用负数的原码来进行减法计算呢？答案是否定的。我还是以3+(-2)为例。

假设我们使用Java中的32位整型来表示2，它的二进制是000…010。最低的两位是10，前面的高位都是0。如果我们使用-2的原码，也就是100…010，然后我们把3的二进制原码000…011和-2的二进制原码100…010相加，会得到100…0101。具体计算你可以看我画的这张图。

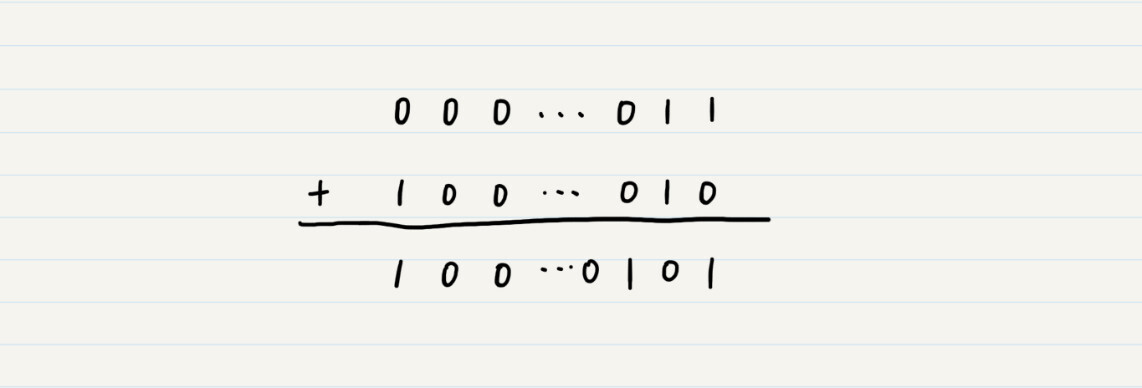
二进制编码上的加减法和十进制类似，只不过，在加法中，十进制是满10才进一位，二进制加法中只要满2就进位；同样，在减法中，二进制借位后相当于2而不是10。

相加后的结果是二进制100…0101，它的最高位是1，表示负数，而最低的3位是101，表示5，所以结果就是-5的原码了，而3+(-2)应该等于1，两者不符。

如果负数的原码并不适用于减法操作，那该怎么办呢？这个问题的解答还要依赖计算机的溢出机制。

我刚刚介绍了溢出以及取模的特性，我们可以充分利用这一点，对计算机里的减法进行变换。假设有i-j，其中j为正数。如果i-j加上取模的除数，那么会形成溢出，并正好能够获得我们想要的i-j的运算结果。如果我说的还是不太好理解，你可以参考下面这张图。

我们把这个过程用表达式写出来就是i-j=(i-j)+(2^n-1+1)=i+(2^n-1-j+1)。

其中2^n-1的二进制码在不考虑符号位的情况下是n-1位的1，那么2^n-1-2的结果就是下面这样的：

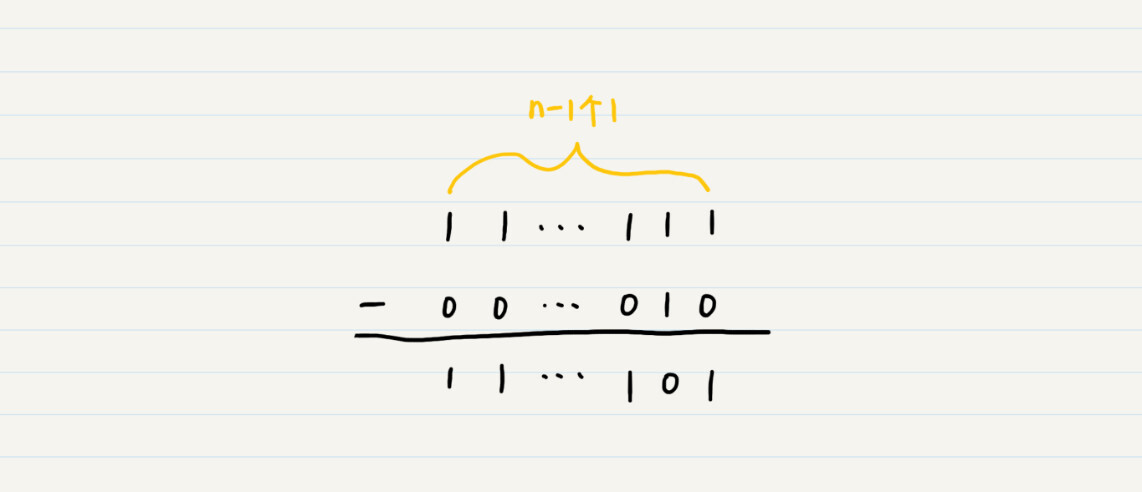
从结果可以观察出来，所谓2^n-1-j相当于对正数j的二进制原码，除了符号位之外按位取反（0变1，1变0）。由于负数-j和正数j的原码，除了符号位之外都是相同的，所以，2^n-1-j也相当于对负数-j的二进制原码，除了符号位之外按位取反。我们把2^n-1-j所对应的编码称为负数-j的反码。所以，-2的反码就是1111…1101。

有了反码的定义，那么就可以得出i-j=i+(2^n-1-j+1)=i的原码+(-j的反码)+1。

如果我们把-j的反码加上1定义为-j的补码，就可以得到i-j=i的原码+(-j的补码)。

由于正数的加法无需负数的加法这样的变换，因此正数的原码、反码和补码三者都是一样的。最终，我们可以得到i-j=i的补码+(-j的补码)。

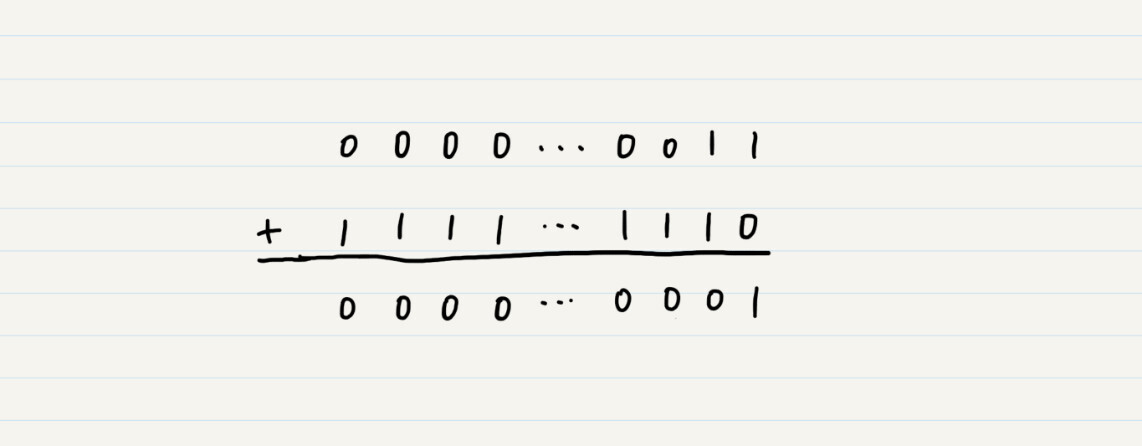
换句话说，计算机可以通过补码，正确地运算二进制减法。我们再来用3+(-2)来验证一下。正数3的补码仍然是0000…0011，-2的补码是1111…1110，两者相加，最后得到了正确的结果1的二进制。

可见，溢出本来是计算机数据类型的一种局限性，但在负数的加法上，它倒是可以帮我们大忙。

最后，给你留一道思考题吧。理解了负数的原码、反码和补码之后，你能算算看，8位的有符号位二进制数10100010，对应的是哪个十进制数吗？

好了，关于二进制的补充内容就到这里了。欢迎你继续留言给我。你也可以点击“请朋友读”，把今天的内容分享给你的好友，和他一起精进。

参考资料

https://learn.lianglianglee.com/%e4%b8%93%e6%a0%8f/%e7%a8%8b%e5%ba%8f%e5%91%98%e7%9a%84%e6%95%b0%e5%ad%a6%e5%9f%ba%e7%a1%80%e8%af%be/%e6%95%b0%e5%ad%a6%e4%b8%93%e6%a0%8f%e8%af%be%e5%a4%96%e5%8a%a0%e9%a4%90%ef%bc%88%e4%b8%80%ef%bc%89%20%e6%88%91%e4%bb%ac%e4%b8%ba%e4%bb%80%e4%b9%88%e9%9c%80%e8%a6%81%e5%8f%8d%e7%a0%81%e5%92%8c%e8%a1%a5%e7%a0%81%ef%bc%9f.md