15 从树到图:如何让计算机学会看地图? 你好,我是黄申。
我们经常使用手机上的地图导航App,查找出行的路线。那计算机是如何在多个选择中找到最优解呢?换句话说,计算机是如何挑选出最佳路线的呢?
前几节,我们讲了数学中非常重要的图论中的概念,图,尤其是树中的广度优先搜索。在广度优先的策略中,因为社交网络中的关系是双向的,所以我们直接用无向边来求解图中任意两点的最短通路。
这里,我们依旧可以用图来解决这个问题,但是,影响到达最终目的地的因素有很多,比如出行的交通工具、行驶的距离、每条道路的交通状况等等,因此,我们需要赋予到达目的地的每条边,不同的权重。而我们想求的最佳路线,其实就是各边权重之和最小的通路。
我们前面说了,广度优先搜索只测量通路的长度,而不考虑每条边上的权重。那么广度优先搜索就无法高效地完成这个任务了。那我们能否把它改造或者优化一下呢?
我们需要先把交通地图转为图的模型。图中的每个结点表示一个地点,每条边表示一条道路或者交通工具的路线。其中,边是有向的,表示单行道等情况;其次,边是有权重的。
假设你关心的是路上所花费的时间,那么权重就是从一点到另一点所花费的时间;如果你关心的是距离,那么权重就是两点之间的物理距离。这样,我们就把交通导航转换成图论中的一个问题:在边有权重的图中,如何让计算机查找最优通路?
基于广度优先或深度优先搜索的方法
我们以寻找耗时最短的路线为例来看看。
一旦我们把地图转换成了图的模型,就可以运用广度优先搜索,计算从某个出发点,到图中任意一个其他结点的总耗时。
基本思路是,从出发点开始,广度优先遍历每个点,当遍历到某个点的时候,如果该点还没有耗时的记录,记下当前这条通路的耗时。如果该点之前已经有耗时记录了,那就比较当前这条通路的耗时是不是比之前少。如果是,那就用当前的替换掉之前的记录。
实际上,地图导航和之前社交网络最大的不同在于,每个结点被访问了一次还是多次。在之前的社交网络的案例中,使用广度优先策略时,对每个结点的首次访问就能获得最短通路,因此每个结点只需要被访问一次,这也是为什么广度优先比深度优先更有效。
而在地图导航的案例中,从出发点到某个目的地结点,可能有不同的通路,也就意味着耗时不同。而耗时是通路上每条边的权重决定的,而不是通路的长度。因此,为了获取达到某个点的最短时间,我们必须遍历所有可能的路线,来取得最小值。这也就是说,我们对某些结点的访问可能有多次。
我画了一张图,方便你理解多条通路对最终结果的影响。这张图中有A、B、C、D、E五个结点,分别表示不同的地点。
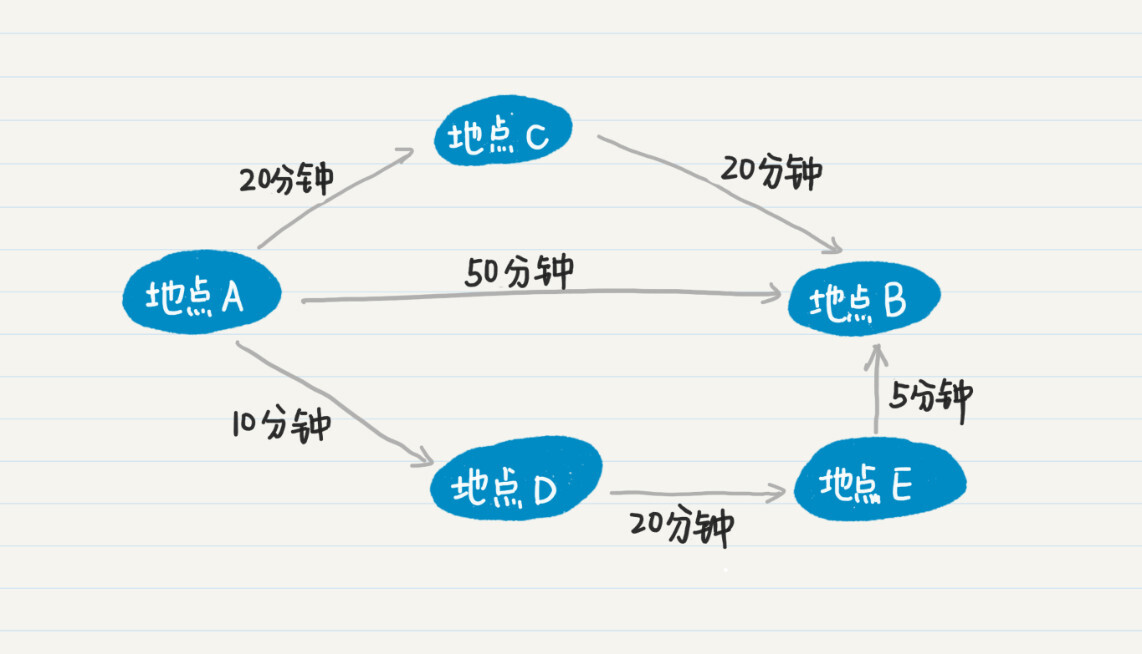
从这个图中可以看出,从A点出发到目的地B点,一共有三条路线。
- 如果你直接从A点到B点,度数为1,需要50分钟。
- 从A点到C点再到B点,虽然度数为2,但总共只要40分钟。
- 从A点到D点,到E点,再到最后的B点,虽然度数为3,但是总耗时只有35分钟,比其他所有的路线更优。
这种情形之下,使用广度优先找到的最短通路,不一定是最优的路线。所以,对于在地图上查找最优路线的问题,无论是广度优先还是深度优先的策略,都需要遍历所有可能的路线,然后取最优的解。
在遍历所有可能的路线时,有几个问题需要注意。
第一,由于要遍历所有可能的通路,因此一个点可能会被访问多次。当然,这个“多次“是指某个结点出现在不同通路中,而不是多次出现在同一条通路中。因为我们不想让用户总是兜圈子,所以需要避免回路。
第二,如果某个结点x和起始点s之间存在多个通路,每当x到s之间的最优路线被更新之后,我们还需要更新所有和x相邻的结点之最优路线,计算复杂度会很高。
一个优化的版本:Dijkstra算法
无论是广度优先还是深度优先的实现,算法对每个结点的访问都可能多于一次。而访问多次,就意味着要消耗更多的计算机资源。那么,有没有可能在保证最终结果是正确的情况下,尽可能地减少访问结点的次数,来提升算法的效率呢?
首先,我们思考一下,对于某些结点,是不是可以提前获得到达它们的最终的解(例如最短耗时、最短距离、最低价格等等),从而把它们提前移出遍历的清单?如果有,是哪些结点呢?什么时候可以把它们移除呢?Dijkstra算法要登场了!它简直就是为了解决这些问题量身定制的。
Dijkstra算法的核心思想是,对于某个结点,如果我们已经发现了最优的通路,那么就无需在将来的步骤中,再次考虑这个结点。Dijkstra算法很巧妙地找到这种点,而且能确保已经为它找到了最优路径。
1.Dijkstra算法的主要步骤
让我们先来看看Dijkstra算法的主要步骤,然后再来理解,它究竟是如何确定哪些结点已经拥有了最优解。
首先你需要了解几个符号。
第一个是source,我们用它表示图中的起始点,缩写是s。
然后是weight,表示二维数组,保存了任意边的权重,缩写为w。w[m, n]表示从结点m到结点n的有向边之权重,大于等于0。如果m到n有多条边,而且权重各自不同,那么取权重最小的那条边。
接下来是min_weight,表示一维数组,保存了从s到任意结点的最小权重,缩写为mw。假设从s到某个结点m有多条通路,而每条通路的权重是这条通路上所有边的权重之和,那么mw[m]就表示这些通路权重中的最小值。mw[s]=0,表示起始点到自己的最小权重为0。
最后是Finish,表示已经找到最小权重的结点之集合,缩写为F。一旦结点被放入集合F,这个结点就不再参与将来的计算。
初始的时候,Dijkstra算法会做三件事情。第一,把起始点s的最小权重赋为0,也就是mw[s] = 0。第二,往集合F里添加结点s,F包含且仅包含s。第三,假设结点 s 能直接到达的边集合为M,对于其中的每一个对端节点m,则把mw[m]设为w[s, m],同时对于所有其他s不能直接到达的结点,将通路的权重设为无穷大。
然后,Dijkstra算法会重复下列两个步骤。
第一步,查找最小mw。从mw数组选择最小值,则这个值就是起始点s到所对应的结点的最小权重,并且把这个点加入到F中,针对这个点的计算就算完成了。
比如,当前mw中最小的值是mw[x]=10,那么结点s到结点x的最小权重就是10,并且把结点x放入集合F,将来没有必要再考虑点x,mw[x]可能的最小值也就确定为10了。
第二步,更新权重。然后,我们看看,新加入F的结点x,是不是可以直接到达其他结点。如果是,看看通过x到达其他点的通路权重,是否比这些点当前的mw更小,如果是,那么就替换这些点在mw中的值。
例如,x可以直接到达y,那么把(mw[x] + w[x, y])和mw[y]比较,如果(mw[x] + w[x, y])的值更小,那么把mw[y]更新为这个更小的值,而我们把x称为y的前驱结点。
然后,重复上述两步,再次从mw中找出最小值,此时要求mw对应的结点不属于F,重复上述动作,直到集合F包含了图的所有结点,也就是说,没有结点需要处理了。
字面描述有些抽象,我用一个具体的例子来解释一下。你可以看我画的这个图。
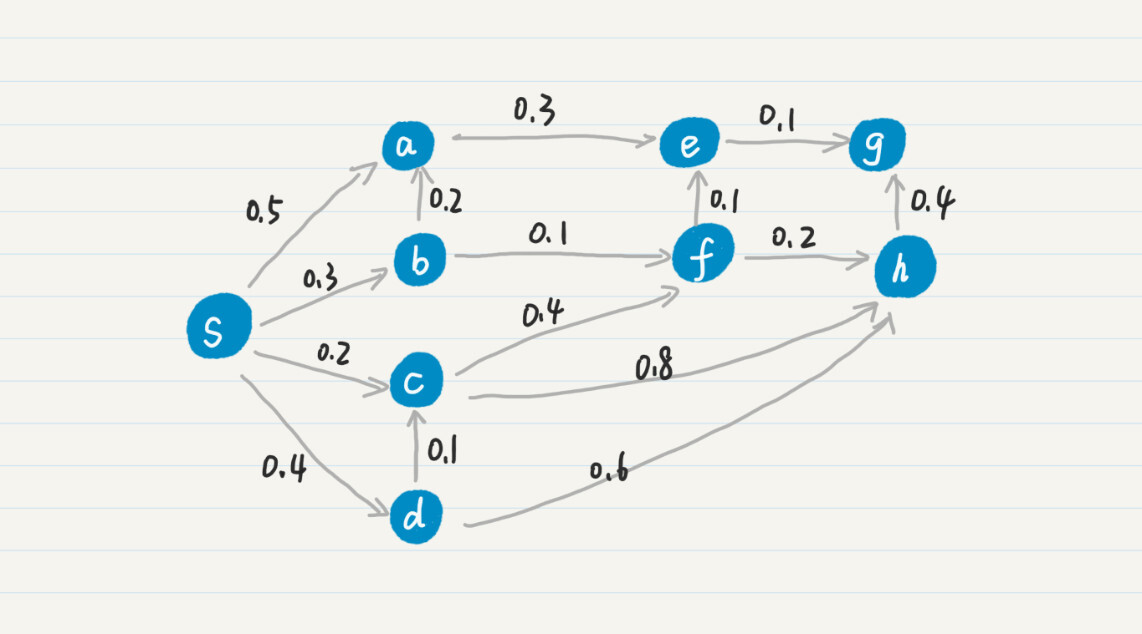
我们把结点s放入集合F。同s直接相连的结点有a、b、c和d,我把它们的mw更新为w数组中的值,就可以得到如下结果:

然后,我们从mw选出最小的值0.2,把对应的结点c加入集合F,并更新和c直接相连的结点f、h的mw值,得到如下结果:

然后,我们从mw选出最小的值0.3,把对应的结点b加入集合F,并更新和b直接相连的结点a和f的mw值。以此逐步类推,可以得到如下的最终结果:
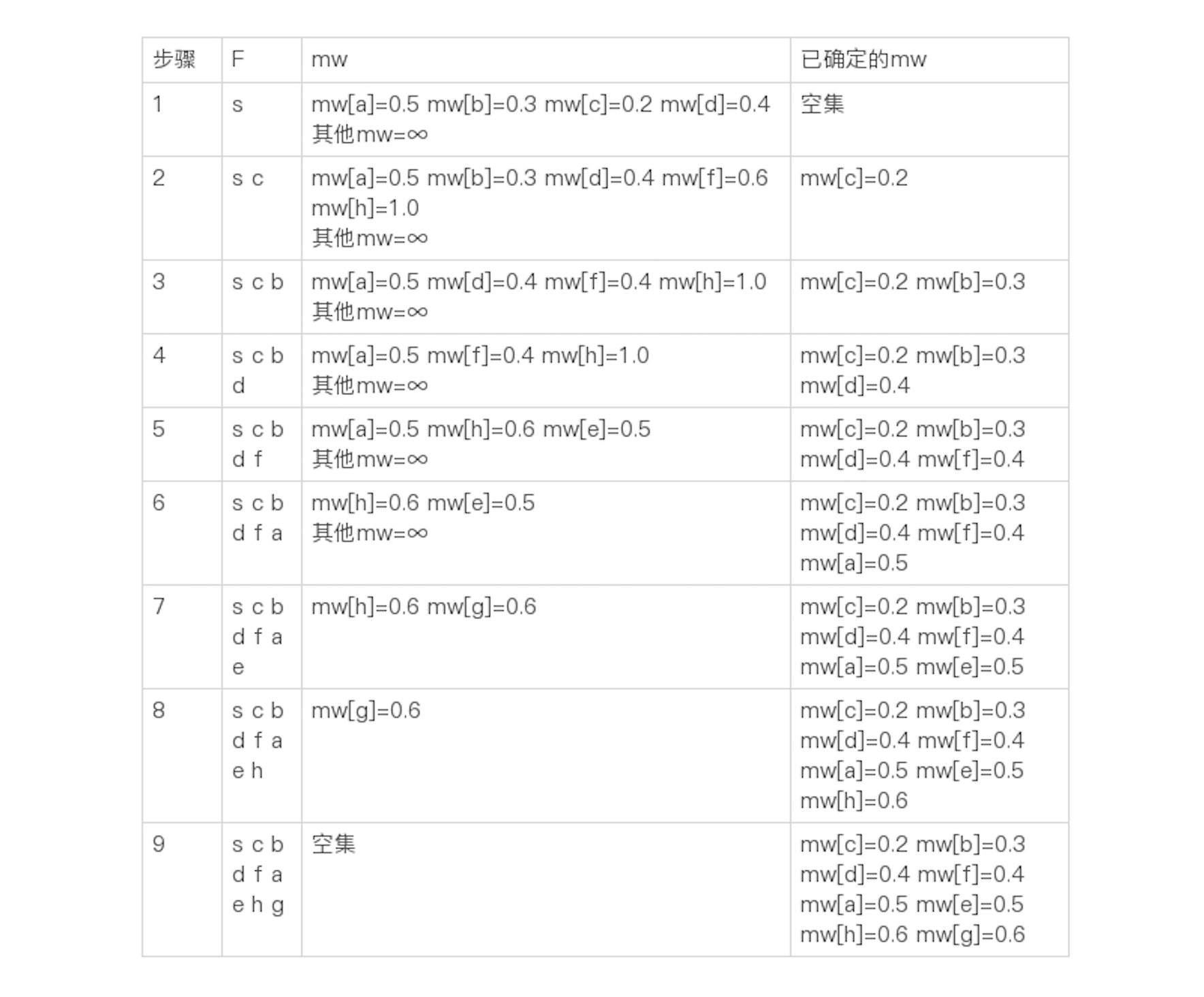
你可以试着自己从头到尾推导一下,看看结果是不是和我的一致。
说到这里,你可能会产生一个疑问:Dijkstra算法提前把一些结点排除在计算之外,而且没有遍历全部可能的路径,那么它是如何确保找到最优路径的呢?
下面,我们就来看看这个问题的答案。Dijkstra算法的步骤看上去有点复杂,不过其中最关键的两步是:第一个是每次选择最小的mw;第二个是,假设被选中的最小mw,所对应的结点是x,那么查看和x直接相连的结点,并更新它们的mw。
2.为什么每次都要选择最小的mw?
最小的、非无穷大的mw值,对应的结点是还没有加入F集合的、且和s有通路的那些结点。假设当前mw数组中最小的值是mw[x],对应的结点是x。如果边的权重都是正值,那么通路上的权重之和是单调递增的,所以其他通路的权重之和一定大于当前的mw[x],因此即使存在其他的通路,其权重也会比mw[x]大。
你可以结合这个图,来理解我刚才这段话。
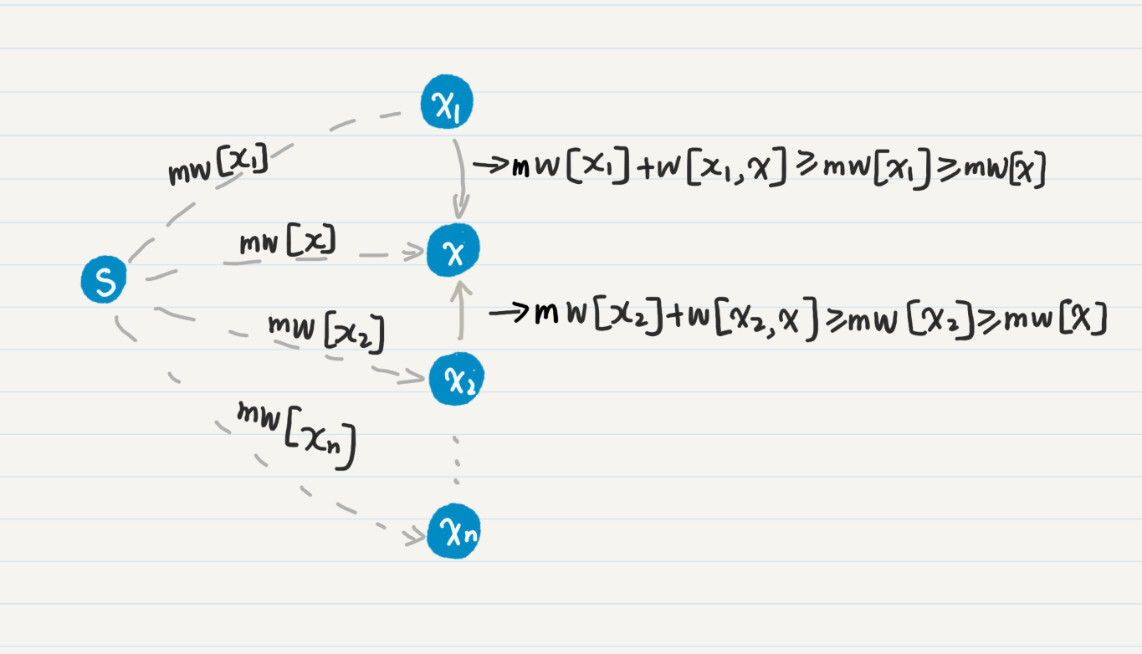
图中的虚线表示省去了通路中间的若干结点。mw[x]是当前mw数组中的最小值,所以它小于等于任何一个mw[xn],其中xn不等于x。
我们假设存在另一个通路,通过(x_{n})达到x,那么通路的权重总和为mw[(x_{n})] + w[(x_{n}), x] ≥ mw[(x_{n})] ≥ mw[x]。所以我们可以得到一个结论:拥有最小mw值的结点x不可能再找到更小的mw值,可以把它放入“已完成“的集合F。
这就是为什么每次都要选择最小的mw值,并认为对应的结点已经完成了计算。和广度优先或者深度优先的搜索相比,Dijkstra算法可以避免对某些结点,重复而且无效的访问。因此,每次选择最小的mw,就可以提升了搜索的效率。
3.为什么每次都要看x直接相连的结点?
我们已经确定mw[x]是从点s到点x的最小权重,那么就可以把这个确定的值传播到和x直接相连、而且不在F中的结点。通过这一步,我们就可以获得从点s到这些点、而且经过x的通路中最小的那个权重。我画了张图帮助你理解。
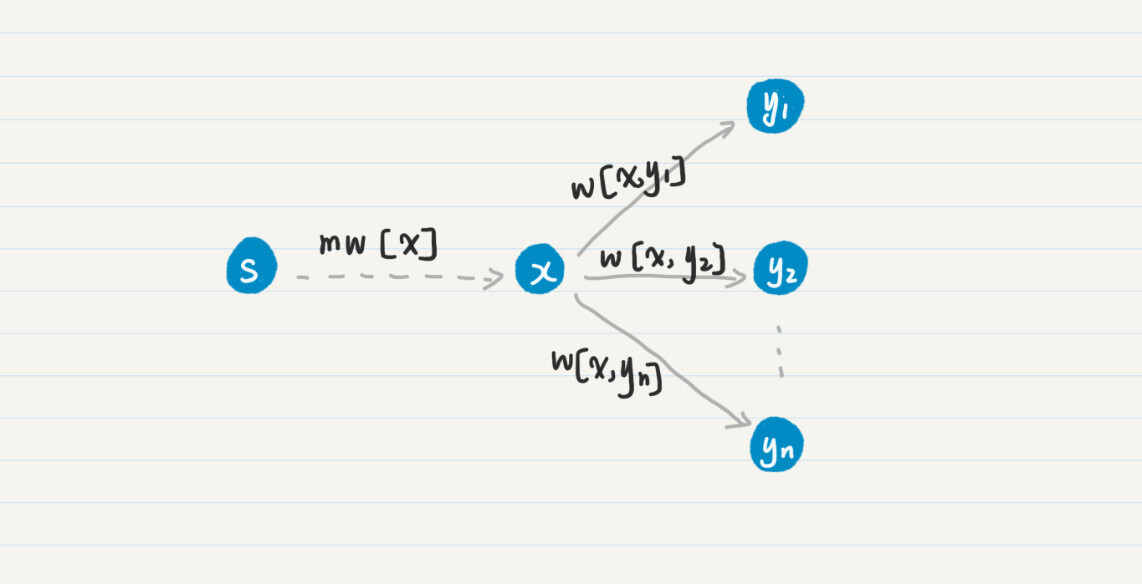
在这个图中,x直接相连(y_{1}),(y_{2}),…,(y_{n})。从点s到点x的mw[x]已经确定了,那么对于从s到yn的所有通路,只有两种可能,经过x和不经过x。如果这条通路经过x,那么其权重的最小值就是mw’[(y_{i})] = mw[x] + w[x, (y_{i})]中的一个(1≤i≤n),我们只需要把这个值和其他未经过x结点的通路之权重对比就足够了。这就是为什么每次要更新和x直接相连的结点之mw。
这一步和广度优先策略中的查找某个结点的所有相邻结点类似。但是,之后,Dijkstra算法重复挑选最小权重的步骤,既没有遵从广度优先,也没有遵从深度优先。即便如此,它仍然保证了不会遗漏任意一点和起始点s之间、拥有最小权重的通路,从而保证了搜索的覆盖率。你可能会奇怪,这是如何得到保证的?我使用数学归纳法,来证明一下。
你还记得数学归纳法的一般步骤吗?刚好借由这个例子我们也来复习一下。
我们的命题是,对于任意一个点,Dijkstra算法都可以找到它和起始点s之间拥有最小权重的通路。
首先,当n=1的时候,也就是只有起始点s和另一个终止点的时候,Dijkstra算法的初始化阶段的第3步,保证了命题的成立。
然后,我们假设n=k-1的时候命题成立,同时需要证明n=k的时候命题也成立。命题在n=k-1时成立,表明从点s到k-1个终点的任何一个时,Dijkstra算法都能找到拥有最小权重的通路。那么再增加一个结点x,Dijkstra算法同样可以为包含x的k个终点找到最小权重通路。
这里我们只需要考虑x和这k-1个点连通的情况。因为如果不连通,就没有必要考虑x了。既然连通,x可能会指向之前k-1个结点,也有可能被这k-1个结点所指向。假设x指向了y,而z指向了x,y和z都是之前k-1个结点中的一员。
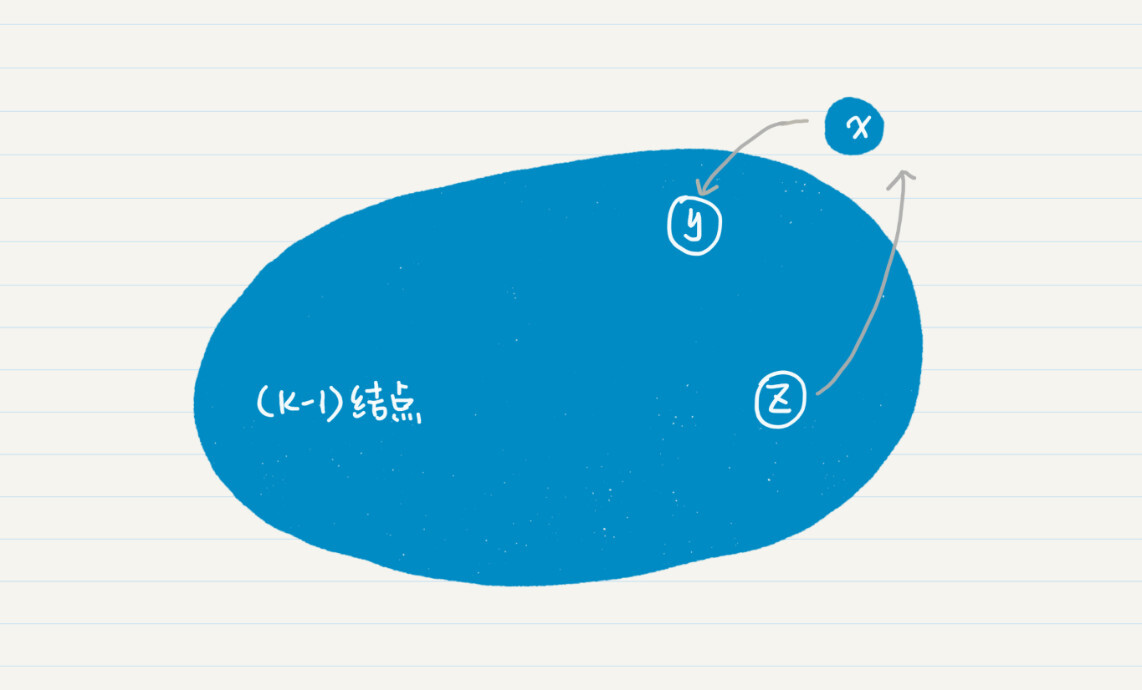
我们先来看x对y的影响。如果x不在从s到y的最小权重通路上,那么x的加入并不影响mw[y]的最终结果。如果x在从s到y的最小权重通路上,那么就意味着mw[x] + w[x, y]≤mw’[y],mw’表示没有引入结点x的时候,mw的值。
所以有mw[x]≤mw’[y],这就意味着Dijkstra算法在查找最小mw的步骤中,会在mw’[y]之前挑出mw[x],也就是找到了从s到y,且经过x的最小权重通路。
我们再来看z对x的影响。假设有多个z指向x,分别是(z_{1}), (z_{2}), …,(z_{m}),从s到x的通路必定会经过这m个z结点中的一个。Dijkstra算法中找最小mw的步骤,一定会遍历mw[(z_{i})](1<=i<=m),而更新权重的步骤,可以并保证从(mw[(z_{i})] + w[(z_{i}), x])中找出最小值,最终找到从s到x的最优通路。
有了详细的推导,想要写出代码就不难了。我这里只给你说几点需要注意的地方。
在自动生成图的函数中,你需要把广度优先搜索的相应代码做两处修改。第一,现在边是有向的了,所以生成的边只需要添加一次;第二,要给边赋予一个权重值,例如可以把边的权重设置为[0,1.0)之间的float型数值。
为了更好地模块化,你可以实现两个函数:findGeoWithMinWeight和updateWeight。它们分别对应于我之前提到的最重要的两步:每次选择最小的mw;更新和x直接相连的结点之mw。
每次查找最小mw的时候,我们需要跳过已经完成的结点,只考虑那些不在F集合中的点。这也是Dijkstra算法比较高效的原因。此外,如果你想输出最优路径上的每个结点,那么在updateWeight函数中就要记录每个结点的前驱结点。
如果你能跟着我进行一步步的推导,并且手写代码进行练习,相信你对Dijkstra算法会有更深刻的印象。
小结
我们使用Dijkstra算法来查找地图中两点之间的最短路径,而今天我所介绍的Dijkstra使用了更为抽象的“权重”。如果我们把结点作为地理位置,边的权重设置为路上所花费的时间,那么Dijkstra算法就能帮助我们找到,任意两个点之间耗时最短的路线。
除了时间之外,你也可以对图的边设置其他类型的权重,比如距离、价格,这样Dijkstra算法可以让用户找到地图任意两点之间的最短路线,或者出行的最低价格等等。有的时候,边的权重越大越好,比如观光车开过某条路线的车票收入。对于这种情况,Dijkstra算法就需要调整一下,每次找到最大的mw,更新邻近结点时也要找更大的值。所以,你只要掌握核心的思路就可以了,具体的实现可以根据情况去灵活调整。

思考题
今天的思考题和地图数据的特殊情况有关。
- 如果边的权重是负数,我们还能用今天讲的Dijkstra算法吗?
- 如果地图中存在多条最优路径,也就是说多条路径的权重和都是相等的,那么我刚刚介绍的Dijkstra算法应该如何修改呢?
欢迎在留言区交作业,并写下你今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。
参考资料
https://learn.lianglianglee.com/%e4%b8%93%e6%a0%8f/%e7%a8%8b%e5%ba%8f%e5%91%98%e7%9a%84%e6%95%b0%e5%ad%a6%e5%9f%ba%e7%a1%80%e8%af%be/15%20%e4%bb%8e%e6%a0%91%e5%88%b0%e5%9b%be%ef%bc%9a%e5%a6%82%e4%bd%95%e8%ae%a9%e8%ae%a1%e7%ae%97%e6%9c%ba%e5%ad%a6%e4%bc%9a%e7%9c%8b%e5%9c%b0%e5%9b%be%ef%bc%9f.md
更多学习
更多实时资讯,前沿技术,生活趣事。尽在【老马啸西风】
交流社群:[交流群信息](https://mp.weixin.qq.com/s/rkSvXxiiLGjl3S-ZOZCr0Q)
