28 数据流分析:你写的程序,它更懂 上一讲,我提到了删除公共子表达式、拷贝传播等本地优化能做的工作,其实,这几个工作也可以在全局优化中进行。
只不过,全局优化中的算法,不会像在本地优化中一样,只针对一个基本块。而是更复杂一些,因为要覆盖多个基本块。这些基本块构成了一个CFG,代码在运行时有多种可能的执行路径,这会造成多路径下,值的计算问题,比如活跃变量集合的计算。
当然了,还有些优化只能在全局优化中做,在本地优化中做不了,比如:
- 代码移动(code motion)能够将代码从一个基本块挪到另一个基本块,比如从循环内部挪到循环外部,来减少不必要的计算。
- 部分冗余删除(Partial Redundancy Elimination),它能把一个基本块都删掉。
总之,全局优化比本地优化能做的工作更多,分析算法也更复杂,因为CFG中可能存在多条执行路径。不过,我们可以在上一节课提到的本地优化的算法思路上,解决掉多路径情况下,V值的计算问题。而这种基于CFG做优化分析的方法框架,就叫做数据流分析。
本节课,我会把全局优化的算法思路讲解清楚,借此引入数据流分析的完整框架。而且在解决多路径情况下,V值的计算问题时,我还会带你学习一个数学工具:半格理论。这样,你会对基于数据流分析的代码优化思路建立清晰的认识,从而有能力根据需要编写自己的优化算法。
数据流分析的场景:活跃性分析
上一讲,我已经讲了本地优化时的活跃性分析,那时,情况比较简单,你不需要考虑多路径问题。而在做全局优化时,情况就要复杂一些:代码不是在一个基本块里简单地顺序执行,而可能经过控制流图(CFG)中的多条路径。我们来看一个例子(例子由if语句形成了两条分支语句):
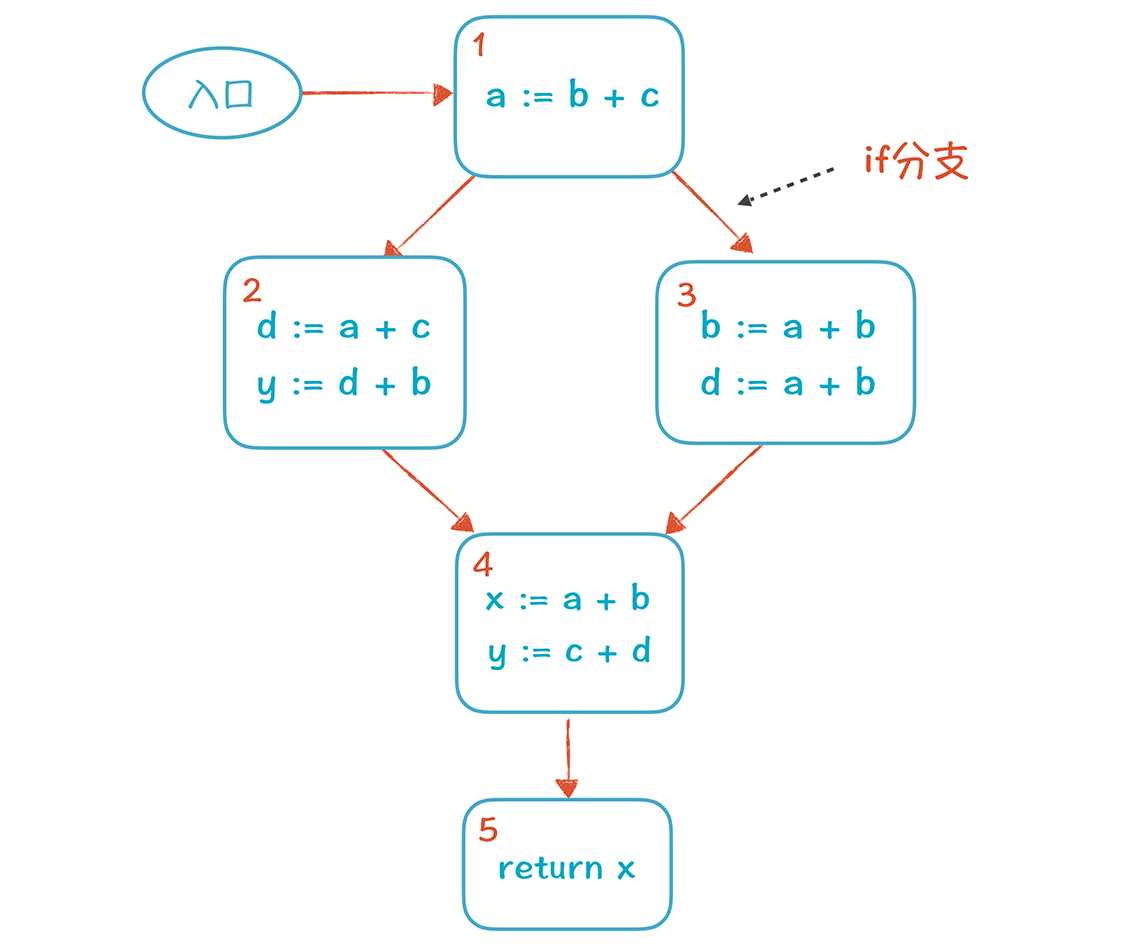
基于这个CFG,我们可以做全局的活跃性分析,从最底下的基本块开始,倒着向前计算活跃变量的集合(也就是从基本块5倒着向基本块1计算)。
这里需要注意,对基本块1进行计算的时候,它的输入是基本块2的输出,也就是{a, b, c},和基本块3的输出,也就是{a, c},计算结果是这两个集合的并集{a, b, c}。也就是说,基本块1的后序基本块,有可能用到这三个变量。这里就是与本地优化不同的地方,我们要基于多条路径来计算。
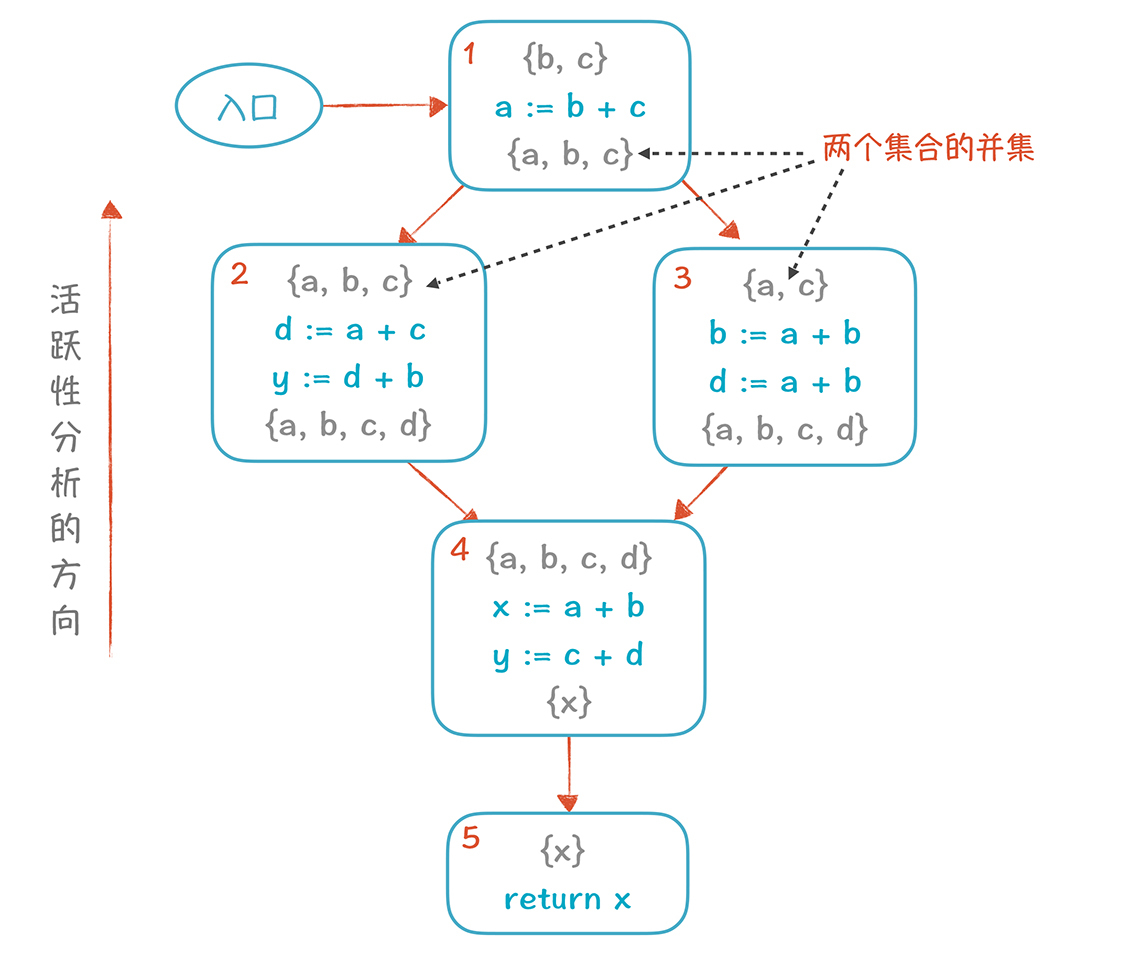
基于这个分析图,我们马上发现y变量可以被删掉(因为它前面的活变量集合{x}不包括y,也就是不被后面的代码所使用),并且影响到了活跃变量的集合。
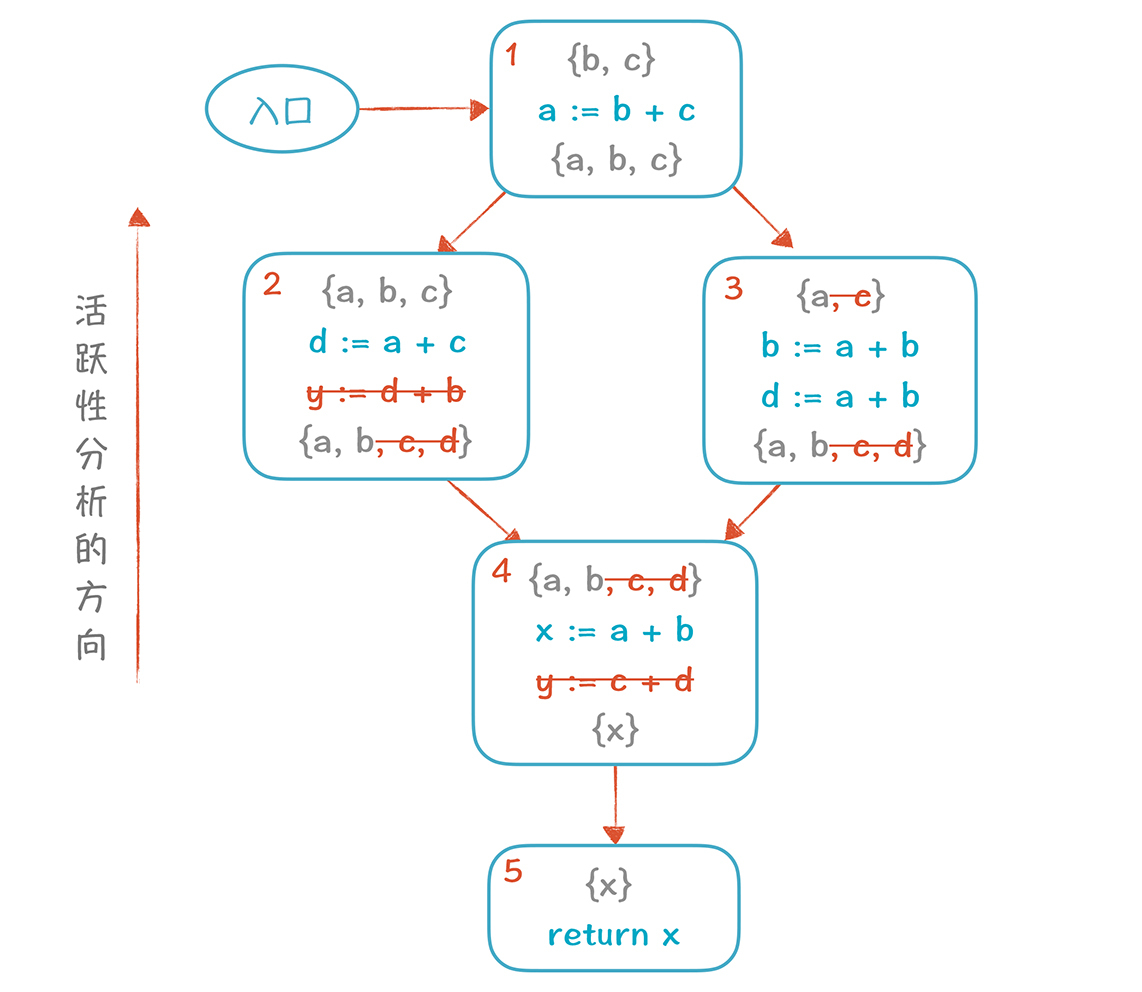
删掉y变量以后,再继续优化一轮,会发现d也可以删掉。
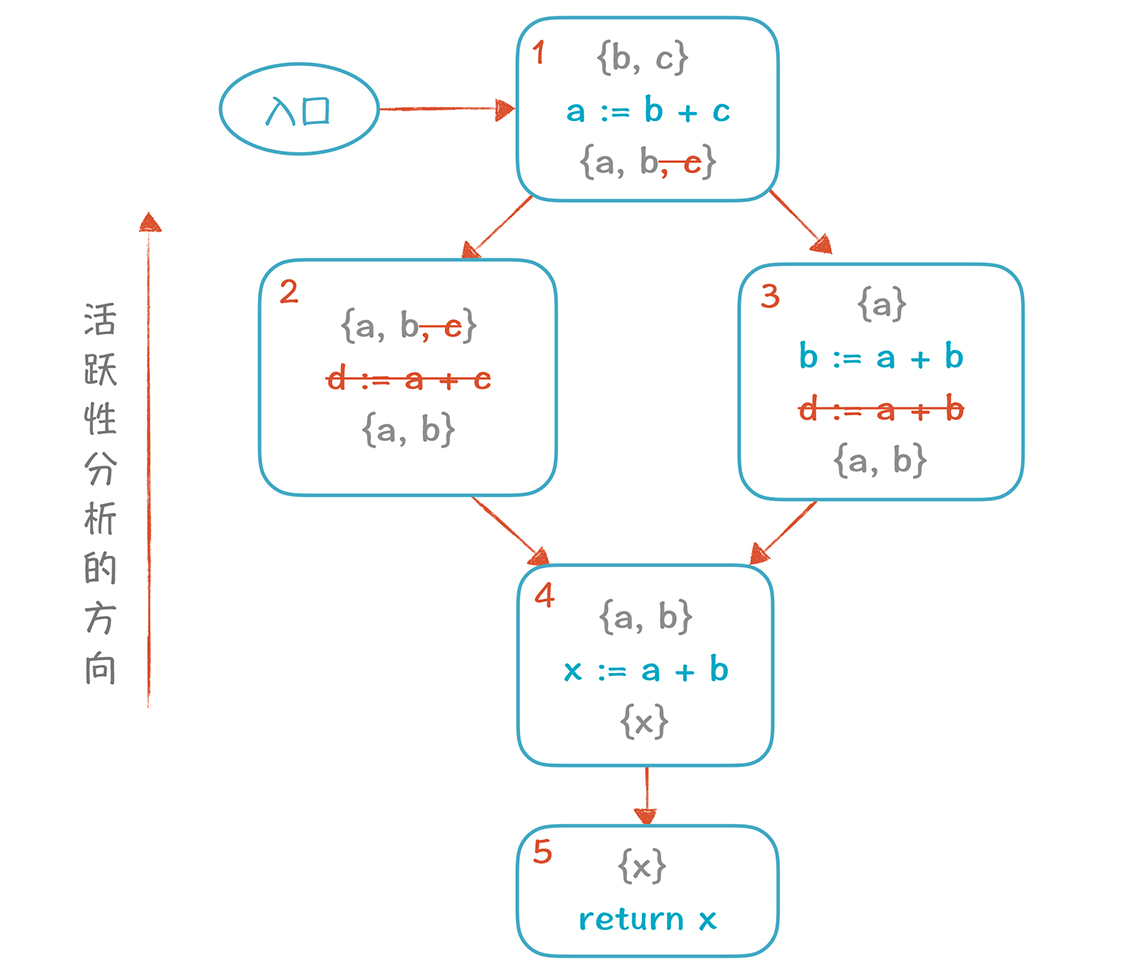
d删掉以后,2号基本块里面已经没有代码了,也可以被删掉,最后的CFG是下面这样:
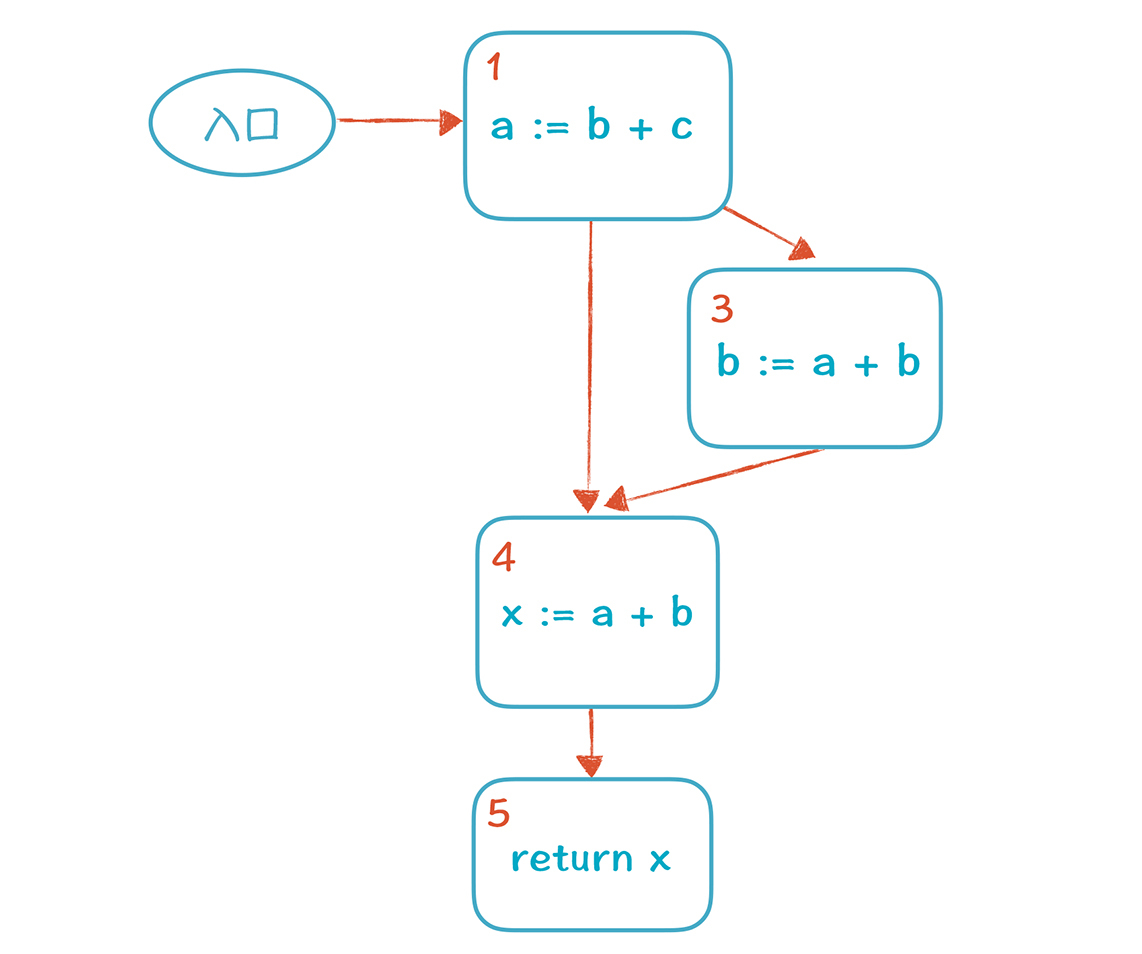
到目前为止,我们发现:全局优化总体来说跟本地优化很相似,唯一的不同,就是要基于多个分支计算集合的内容(也就是V值)。在进入基本块1时,2和3两个分支相遇(meet),我们取了2和3V值的并集。这就是数据流分析的基本特征,你可以记住这个例子,建立直观印象。
但是,上面这个CFG还是比较简单的,因为它没有循环,属于有向无环图。这种图的特点是:针对图中的每一个节点,我们总能找到它的前序节点和后序节点,所以我们只需要按照顺序计算就好了。但是如果加上了环路,就不那么简单了,来看一看下面这张图:
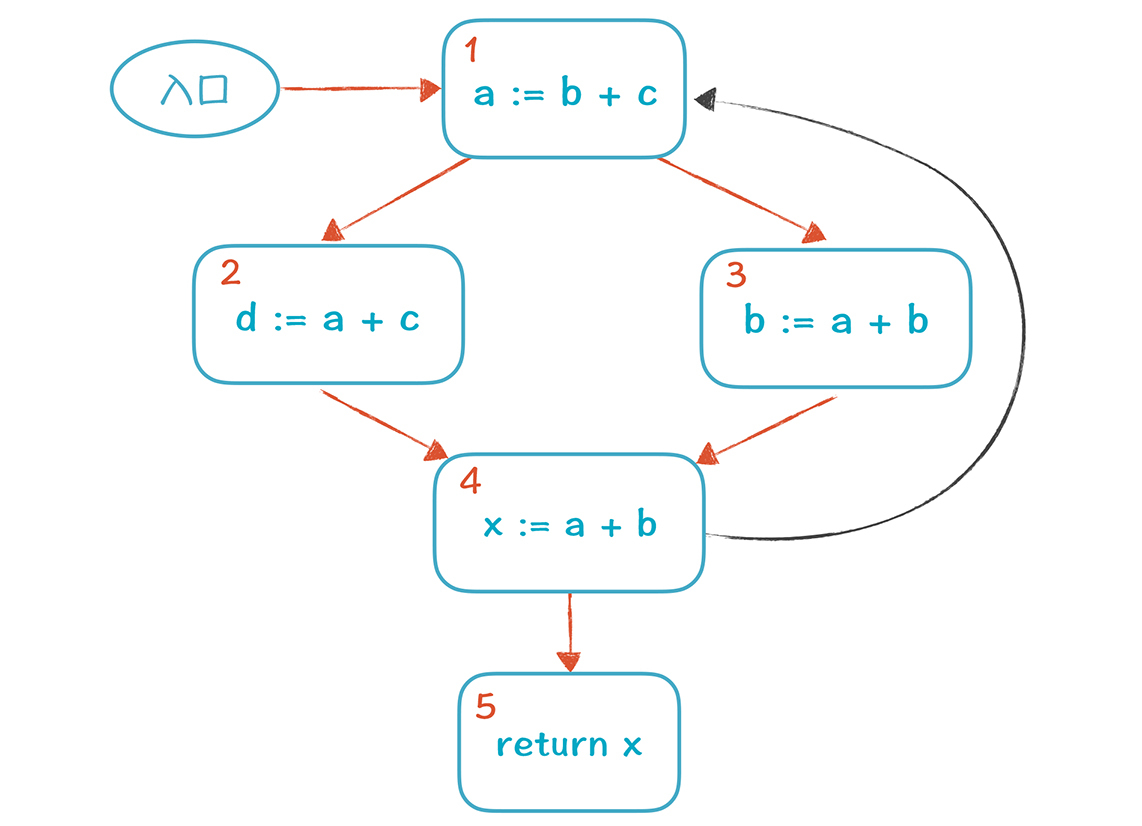
基本块4有两个后序节点,分别是5和1,所以要计算4的活跃变量,就需要知道5和1的输出是什么。5的输出好说,但1的呢?还没计算出来呢。因为要计算1,就要依赖2和3,从而间接地又依赖了4。这样一来,1和4是循环依赖的。再进一步探究的话,你发现其实1、2、3、4四个节点之间,都是循环依赖的。
所以说,一旦在CFG中引入循环回路,严格的前后计算顺序就不存在了。那你要怎么办呢?
其实,我们不是第一次面对这个处境了。在前端部分,我们计算First和Follow集合的时候,就会遇到循环依赖的情况,只不过那时候没有像这样展开,细细地分析。不过,你可以回顾一下17讲和18讲,那个时候你是用什么算法来破解僵局的呢?是不动点法。在这里,我们还是要运用不动点法,具体操作是:给每个基本块的V值都分配初始值,也就是空集合。
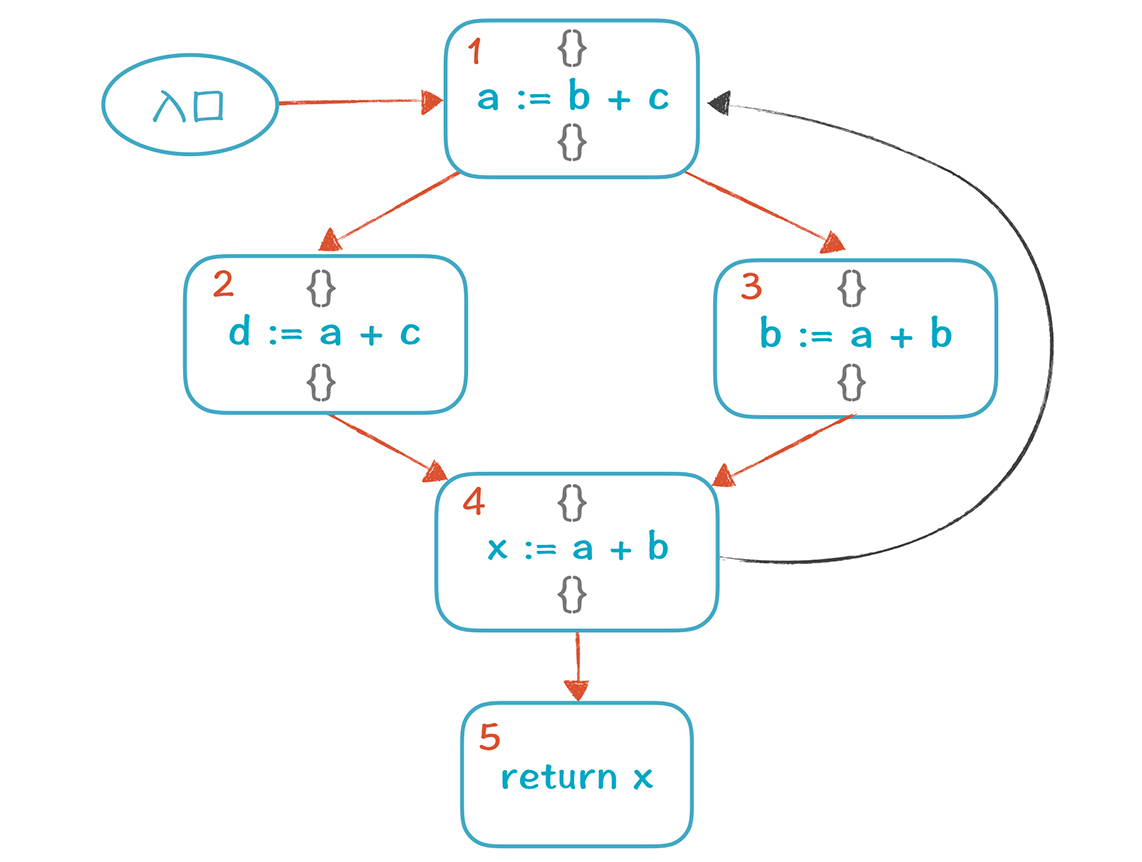
然后对所有节点进行多次计算,直到所有集合都稳定为止。第一遍的时候,我们按照5-4-3-2-1的顺序计算(实际上,采取任何顺序都可以),计算结果如下:
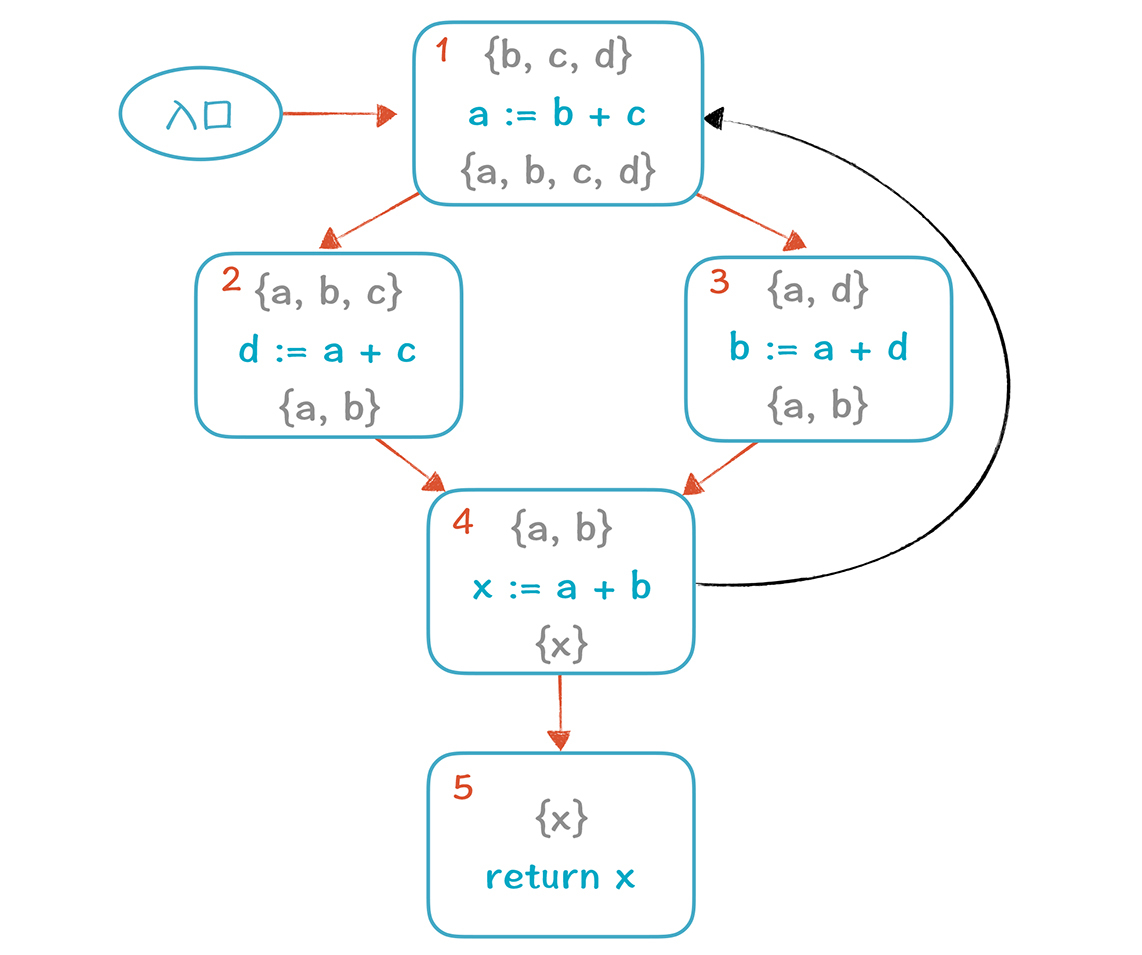
如果现在计算就结束,我们实际上可以把基本块2中的d变量删掉。但如果我们再按照5-4-3-2-1的顺序计算一遍,就会往集合里增加一些新的元素(在图中标的是橙色)。这是因为,在计算基本块4的时候,基本块1的输出{b, c, d}也会变成4的输入。这时,我们发现,进入基本块2时,活变量集合里是含有d的,所以d是不能删除的。
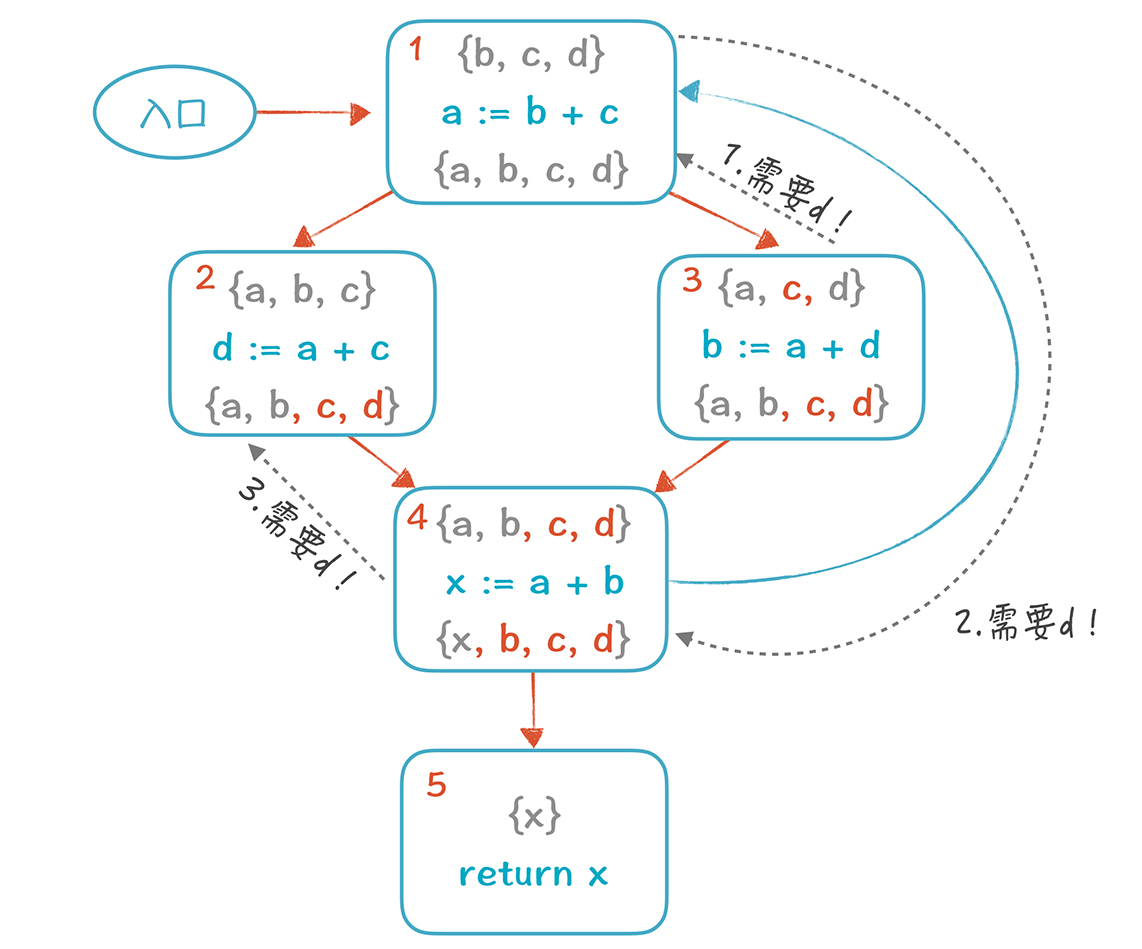
你再仔细看看,这个d是哪里需要的呢?是基本块3需要的:它会跟1去要,1会跟4要,4跟2要。所以,再次证明,1、2、3、4四个节点是互相依赖的。
我们再来看一下,对于活变量集合的计算,当两个分支相遇的情况下,最终的结果我们取了两个分支的并集。
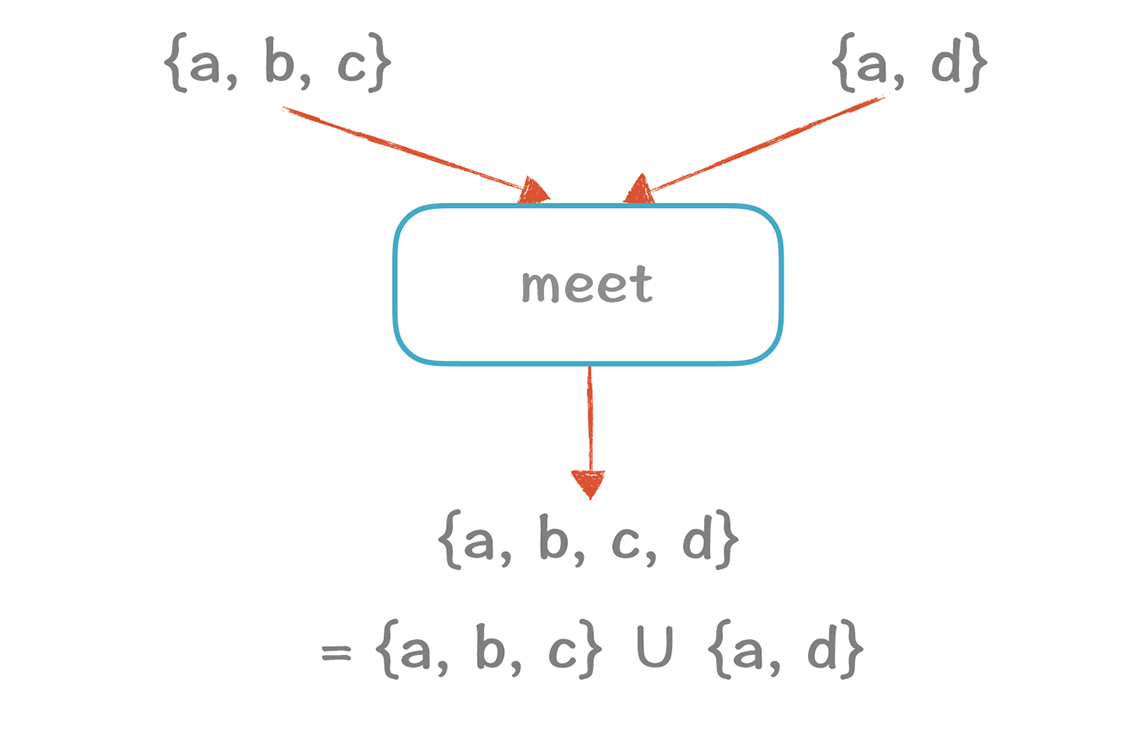
在上一讲,我们说一个本地优化分析包含四个元素:方向(D)、值(V)、转换函数(F)和初始值(I)。在做全局优化的时候,我们需要再多加一个元素,就是两个分支相遇的时候,要做一个运算,计算他们相交的值,这个运算我们可以用大写的希腊字母Λ(lambda)表示。包含了D、V、F、I和Λ的分析框架,就叫做数据流分析。
那么Λ怎么计算呢?研究者们用了一个数学工具,叫做“半格”(Semilattice),帮助做Λ运算。
直观地理解半格理论
如果要从数学理论角度完全把“半格”这个概念说清楚,需要依次介绍清楚“格”(Lattice)、“半格”(Semilattice)和“偏序集”(Partially Ordered Set)等概念。我想这个可以作为爱好数学的同学的一个研究题目,或者去向离散数学的老师求教。在我们的课程里,我只是通过举例子,让你对它有直观的认识。
首先,半格是一种偏序集。偏序集就是集合中只有部分成员能够互相比较大小。举例来说会比较直观。在做全局活跃性分析的时候,{a, b, c}和{a, c}相遇,产生的新值是{a, b, c}。我们形式化地写成{a, b, c} Λ {a, c} = {a, b, c}。
这时候我们说{a, b, c}是可以跟{a, c}比较大小的。那么哪个大哪个小呢? 如果XΛY=X,我们说X<=Y。
所以,{a, b, c}是比较小的,{a, c}是比较大的。
当然,{a, b, c}也可以跟{a, b}比较大小,但它没有办法跟{c, d}比较大小。所以把包含了[{a, b, c}、{a, c}、{a, b}、{c, d}…]这样的一个集合,叫做偏序集,它们中只有部分成员之间可以比较大小。哪些成员可以比较呢?就是下面的半格图中,可以通过有方向的线连起来的。
半格可以画成图形,理解起来更直观,假设我们的程序只有a, b, c三个变量,那么这个半格画成图形是这样的:
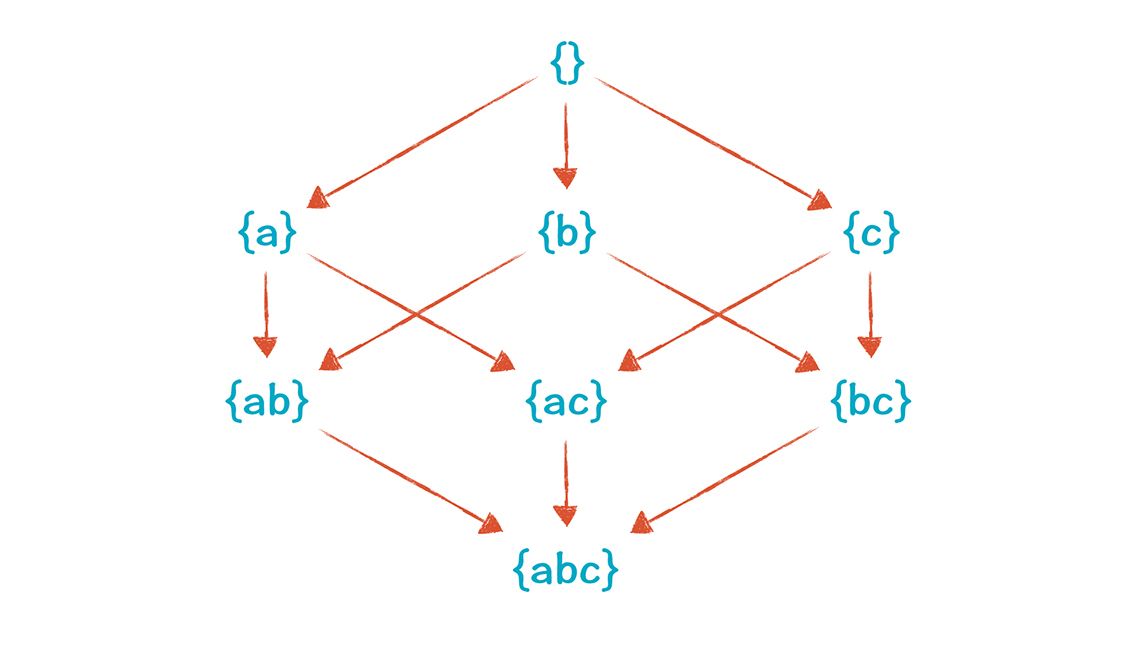
沿着上面图中的线,两个值是可以比较大小的,按箭头的方向依次减少:{}>{a}>{a, b}> {a, b, c}。如果两个值之间没有一条路径,那么它们之间就是不能比较大小的,就像{a}和{b}就不能比较大小。
对于这个半格,我们把{}(空集)叫做Top,Top大于所有的其他的值。而{a, b, c}叫做Bottom,它是最小的值。
在做活跃性分析时,我们的Λ运算是计算两个值的最大下界(Greatest Lower Bound)。怎么讲呢?就是比两个原始值都小的值中,取最大的那个。{a}和{b}的最大下界是{a, b},{a, b, c} 和{a, c}的最大下界就是{a, b, c} 。
- 如果一个偏序集中,任意两个元素都有最大下界,那么这个偏序集就叫做交半格(Meet Semilattice)。
- 与此相对应的,如果集合中的每个元素都有最小上界(Least Upper Bound),那么这个偏序集叫做并半格(Join Semilattice)。
- 如果一个偏序集既是交半格,又是并半格,我们说这个偏序集是一个格,示例的这个偏序集就是一个格。
你可能会奇怪,为什么要引入这么复杂的一套数学工具呢?不就是集合运算吗?两个分支相遇,就计算它们的并集,不就可以了吗?事情没那么简单。因为并不是所有的分析,其V值都是一个集合,就算是集合,相交时的运算也不一定是求并集,而有可能是求交集。
我们通过另一个案例来分析一下非集合的半格运算:常数传播。
数据流分析的场景:常数传播
常数传播,就是如果知道某个变量的值是个常数,那么就把用到这个变量的表达式,都用常数去替换。看看下面的例子,在基本块4中,a的值能否用一个常数替代?
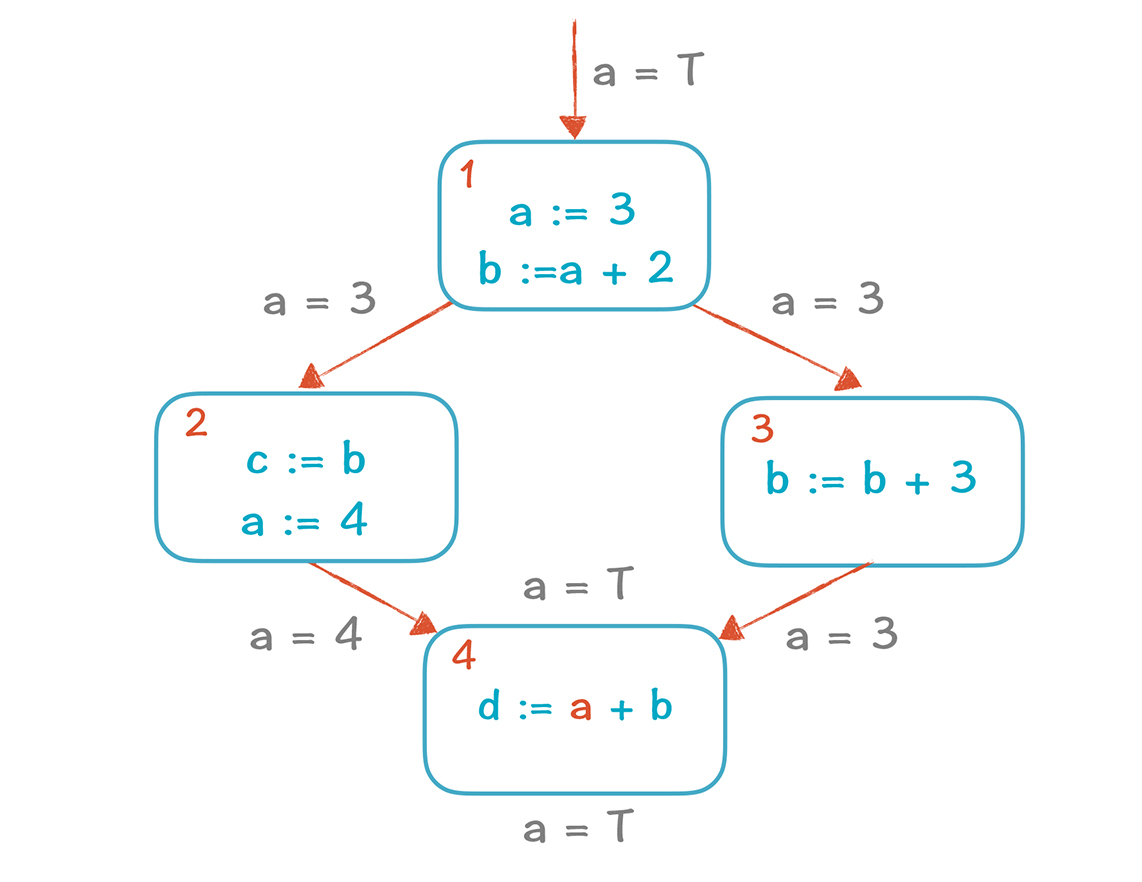
答案是不能。到达基本块4的两条路径,一条a=3,另一条a=4。我们不知道在实际运行的时候,会从哪条路径过来,所以这个时候a的取值是不确定的,基本块4中的a无法用常数替换。
那么,运用数据流分析的框架怎么来做常数传播分析呢?
在这种情况下,V不再是一个集合,而是a可能取的常数值,但a有可能不是一个常数啊,所以我们再定义一个特殊的值:Top(T)。
除了T之外,我们再引入一个与T对应的特殊值:Bottom(它的含义是,某个语句永远不会被执行)。总结起来,常数传播时,V的取值可能是3个:
- 常数c
- Top:意思是a的值不是一个常数
- Bottom:某个语句不会被执行。
这些值是怎么排序的呢?最大的是Top,中间各个常数之间是无法比较的,Bottom是最小的。
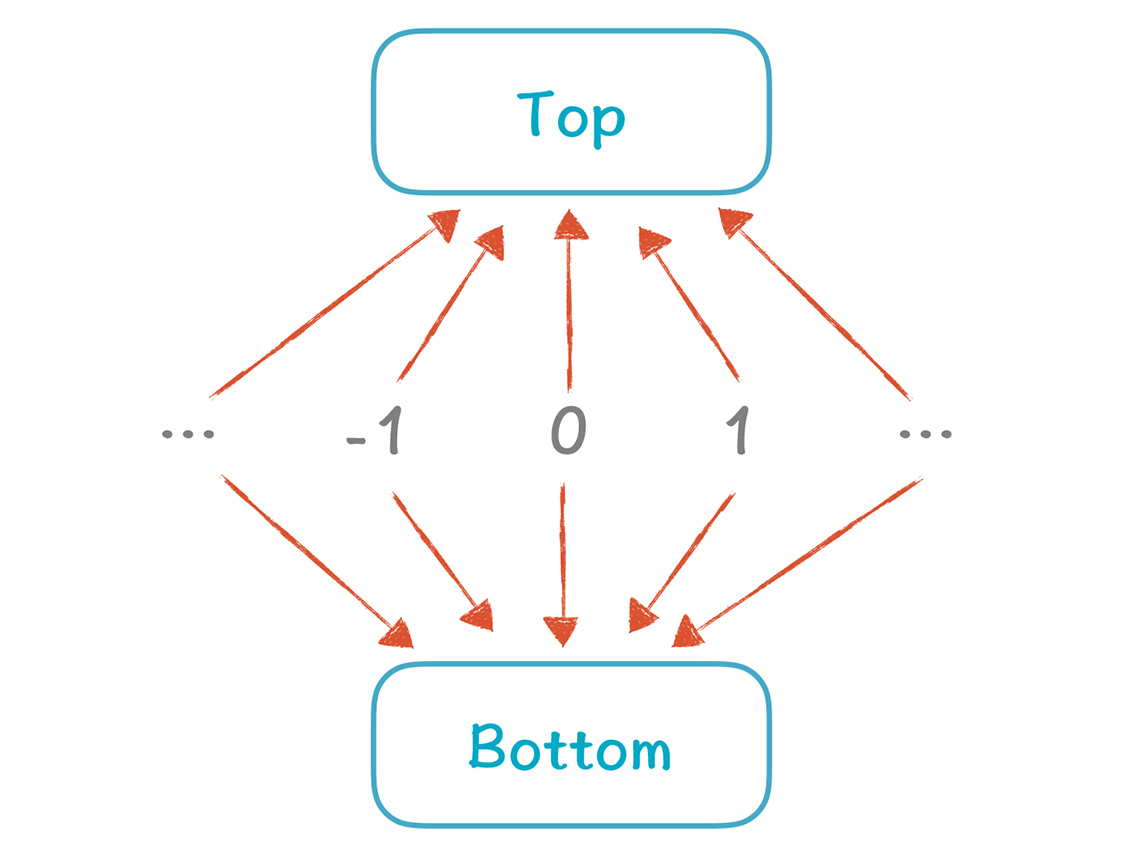
接下来,我们看看如何计算多个V值相交的值。
我们再把计算过程形式化一下。在这个分析中,当我们经过每个语句的时候,V值都可能发生变化,我们用下面两个函数来代表不同地方的V值:
- C(a, s, in)。表示在语句s之前a的取值,比如,C(a, b:=a+2, in) = 3。
- C(a, s, out)。表示在语句s之后a的取值,比如,C(a, a:=4, out) = 4。
如果s的前序有i条可能的路径,那么多个输出和一个输入“C(a, si, out)和C(a, s, in)”的关系,可以制定一系列规则:
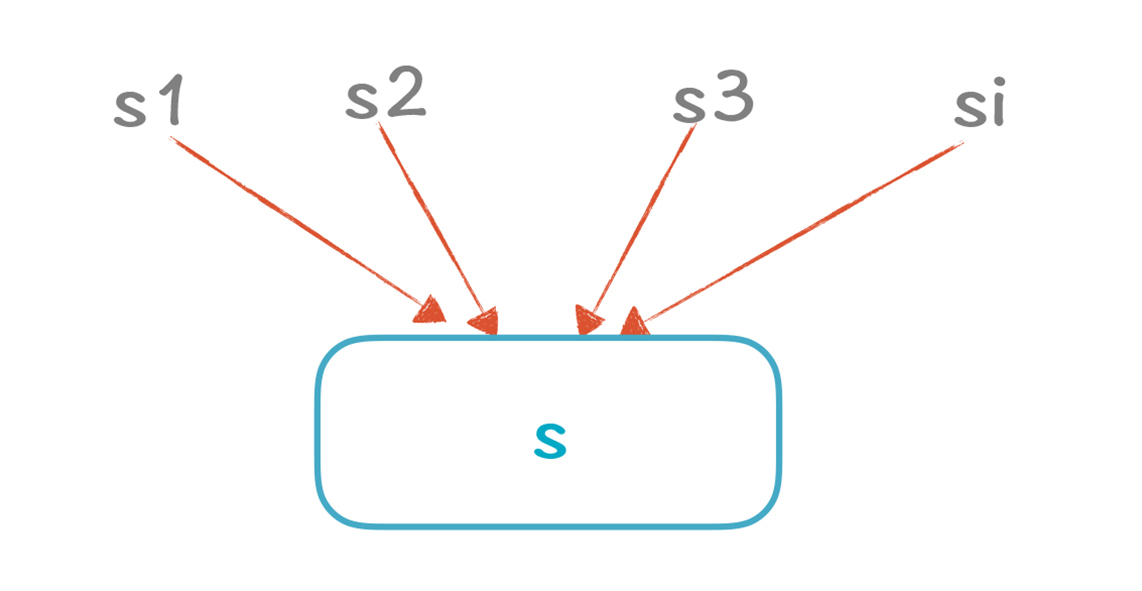
1.如果有一条输入路径是Top,或者说C(a, si, out)是Top,那么结果C(a, s, in)就是Top。
2.如果输入中有两个不同的常数,比如3和4,那么结果也是Top(我们的示例就是这种情况)。
3.如果所有的输入都是相同的常数或Bottom,那么结果就是该常数。如果所有路径a的值都是3,那么这里就可以安全地认为a的值是3。那些Bottom路径不影响,因为整条路径不会执行。
4.如果所有的输入都是Bottom,那么结果也是Bottom。
上面的这4个规则,就是一套半格的计算规则。
在这里,我们也可以总结一下它的转换规则,也就是F,考虑一下某个Statement的in值和out值的关系,也就是经过该Statement以后,V值会有啥变化:
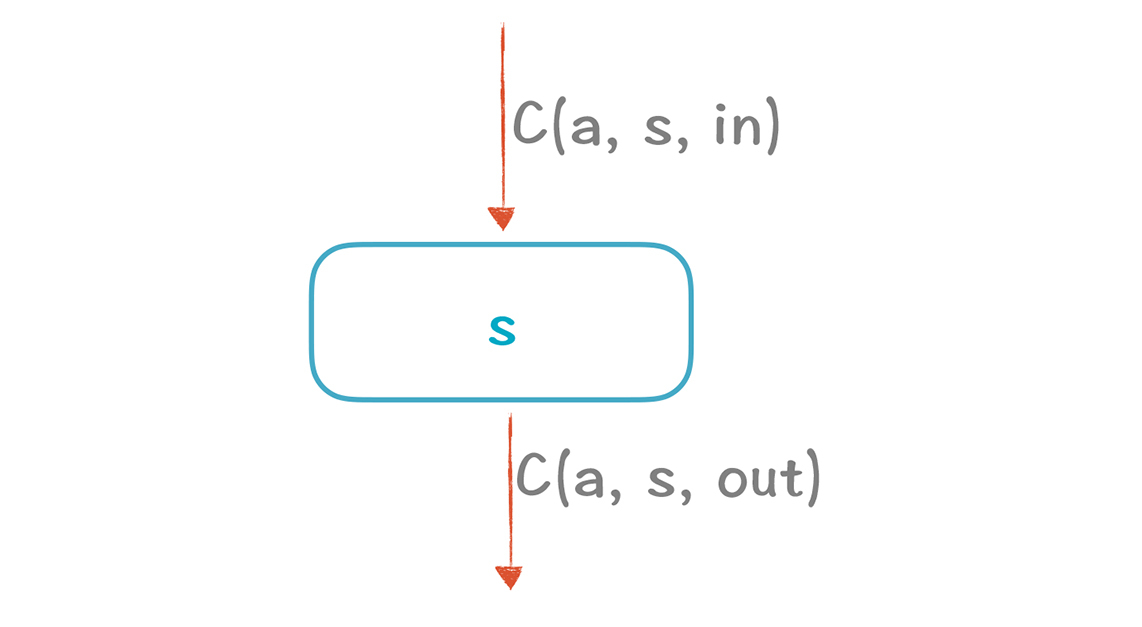
1.如果输入是Bottom,那么输出也是Bottom。也就是这条路径不会经过。- 2.如果该Statement就是“ a := 常数”,那么输出就是该常数。- 3.如果该Statement是a赋予的一个比较复杂的表达式,而不是常数,那么输出就是Top。- 4.如果该Statement不是对a赋值的,那么V值保持不变。
好了,转换函数F也搞清楚了。初始值I是什么呢?是Top,因为一开始的时候,a还没有赋值,所以不会是常数;方向D是什么呢?D是向下。这个时候,D、V、F、I和Λ5个元素都清楚了,我们就可以写算法实现了。
课程小结
本节课,我们基于全局优化分析的任务,介绍了数据流分析这个框架,并且介绍了半格这个数学工具。我希望你在本讲记住几个要点:
- 全局分析比本地分析多处理的部分就是CFG,因为有了多条执行分支,所以要计算分支相遇时的值,当CFG存在环路的时候,要用不动点法来计算出所有的V值。
- 数据流分析框架包含方向(D)、值(V)、转换函数(F)、初始值(I)和交运算(Λ)5个元素,只要分析清楚这5个元素,就可以按照固定的套路来编写分析程序。
- 对于半格理论,关键是要知道如何比较偏序集中元素的大小,理解了这个核心概念,那么求最大下界、最小上界这些也就没有问题了。
数据流分析也是一个容易让学习者撞墙的知识点,特别是再加上“半格”这样的数学术语的时候。不过,我们通过全局活跃性分析和全局常数传播的示例,对“半格”的抽象数学概念建立了直觉的理解。遇到全局分析的任务,你也应该能够比照这两个示例,设计出完整的数据流分析的算法了。不过我建议你,还是要按照上一讲中对LLVM优化功能的介绍,多做几个例子实验一下。
一课一思
如果我们想做一个全局分析,用于删除公共子表达式,它的数据流分析框架应该是怎样的?也就是D、V、F、I和Λ各自应该如何设计呢?欢迎分享你的想法。
最后,感谢你的阅读,如果这篇文章让你有所收获,也欢迎你将它分享给更多的朋友。
参考资料
https://learn.lianglianglee.com/%e4%b8%93%e6%a0%8f/%e7%bc%96%e8%af%91%e5%8e%9f%e7%90%86%e4%b9%8b%e7%be%8e/28%20%e6%95%b0%e6%8d%ae%e6%b5%81%e5%88%86%e6%9e%90%ef%bc%9a%e4%bd%a0%e5%86%99%e7%9a%84%e7%a8%8b%e5%ba%8f%ef%bc%8c%e5%ae%83%e6%9b%b4%e6%87%82.md
更多学习
更多实时资讯,前沿技术,生活趣事。尽在【老马啸西风】
交流社群:[交流群信息](https://mp.weixin.qq.com/s/rkSvXxiiLGjl3S-ZOZCr0Q)
