12 JS语义分析该用迭代还是递归? 你好,我是石川。
在前面两讲中,我们学习了JavaScript语言的数据类型,通过堆栈的数据结构了解了闭包的原理。这一讲,我们来聊聊算法。前面我们在讲到编程模式时提到,如果说函数式编程是输入、计算和输出,那中间的计算部分就可能用到算法了。而迭代和递归可以说是非常基础的算法。
迭代相对比较好理解,只要用过for loop的话,你对它就不会太陌生,而递归比较难理解。但和闭包一样,一旦你掌握了它的运用技巧,就会体会到它的强大之处。
我们在讲到函数式编程的时候,也说过一个很重要的思想就是“副作用”,而递归就自带很多副作用,相应地也出现了很多的解决方案。今天,我们就来看看它都有哪些副作用,以及解决这些副作用我们可以用哪些方法。
那在这之前,我们先来看看迭代和递归分别是什么。
迭代和递归的区别
首先我们得搞清楚迭代和递归有什么区别?
先说迭代,举个例子。做过软件工程的同学都经历过迭代吧,如果是一个敏捷的项目,它的过程就是一个小步快跑的过程,功能不是一下子都做出来的,而是根据优先级,先做优先级高的,再做优先级低的。这就是一个通过循环往复不断完善的过程。
而递归呢,就好比我们寄快递。寄出去的过程是递,收到签收的回执就是归,但是这个过程中间可不只一个人,而是在寄出去的过程,是一个人先运到中转站,再有人运到联络处,最后才到我们手中。哪怕回去的回执是电子的,但在网络世界里,信息的传递也是需要经过每个节点。这样的一去一回就是递归。
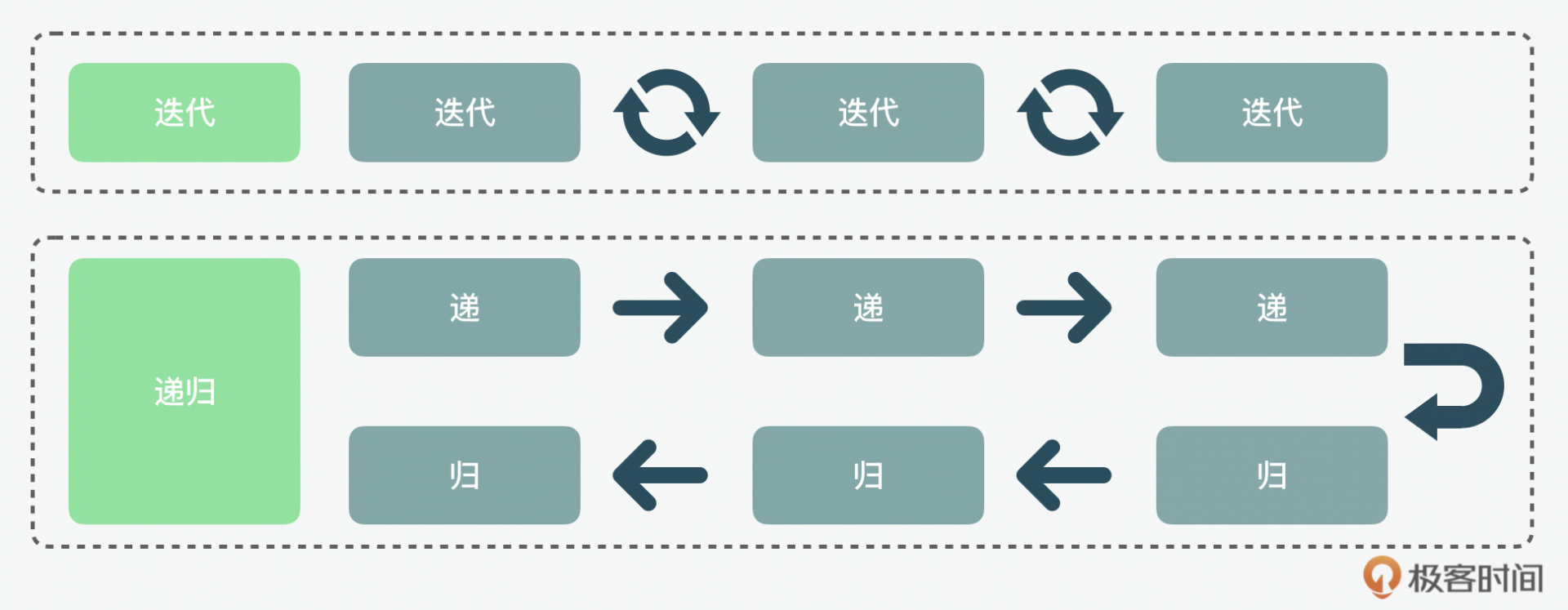
而同样的一个问题,我们可能既可以用迭代的方式来做,也可以用递归的方式来做。
比如我们要计算阶乘。7的阶乘是“7!”,等于 7 /* 6 /* 5 /* 4 /* 3 /* 2 /* 1,结果是5040。如果用一个迭代函数来计算,大概是如下的方式。在每一次的迭代循环过程中,我们都用之前的乘积乘以下一个要迭代的 n 递减的数字。 function factorialIterative(number) { if (number < 0) return undefined; let total = 1; for (let n = number; n > 1; n–) { total = total /* n; } return total; } console.log(factorialIterative(7)); // 5040
如果我们用递归的方式来解决会是什么样子呢?
在递归里面,通常有两个基本元素,一个是基本条件(base case),也叫做终止条件(stop point);另外一个是递归本身。
现在我们可以看到,如果我们把上面的例子转变成递归的形式,即如下。在递归中调用的函数一般就是函数本身。 function factorialRecursive(n) { // 基本条件 if (n === 1 || n === 0) { return 1; } // 递归调用 return n /* factorialRecursive(n - 1); } console.log(factorialRecursive(7)); // 5040
上面这段代码在执行中如下。我们可以看到前面7步,都是递的过程。在碰到基本条件后,开始了归的过程。

递归中用到的分治
下面我们再来用经典的斐波那契(Fibonacci Sequence)数列对比下迭代和递归。斐波那契数列的特点就是这个数列从第3项开始,每一项都等于前两项之和。按照这样的规则,到第10项的时候,相加的值应该是55。 1,1,2,3,5,8,13,21,34,55
如果用迭代的方式来写计算第n项的斐波那契数的函数的话,大致如下:
function fibIterative(n) { if (n < 1) return 0; if (n <= 2) return 1; let fibNMinus2 = 0; let fibNMinus1 = 1; let fibN = n; // n >= 2 for (let i = 2; i <= n; i++) { // f(n-1) + f(n-2) fibN = fibNMinus1 + fibNMinus2; fibNMinus2 = fibNMinus1; fibNMinus1 = fibN; } return fibN; } console.log(fibIterative(10)); // 55
如果我们使用的是递归的话,从代码上看就简洁多了。在这里我们也使用了另外一个核心算法思想,就是分治(divide and conquer)。分治的意思就是分而治之。因为前面我们说了,斐波那契数列的特点就是这个数列从第3项开始,每一项都等于前两项之和。所以在这里,我们就先分别调用fibRecursive(n - 1)和fibRecursive(n - 2)这两个递归函数来分别计算前两项,之后我们再把它们相加,得到最终的结果。
function fibRecursive(n){ // 基本条件 if (n < 1) return 0; // 基本条件 if (n <= 2) return 1; // 递归+分治 return fibRecursive(n - 1) + fibRecursive(n - 2); } console.log(fibRecursive(10)); // 55
但是这里有一个问题,当我们在计算fibRecursive(5)的时候,fibRecursive(3)被计算了两次。
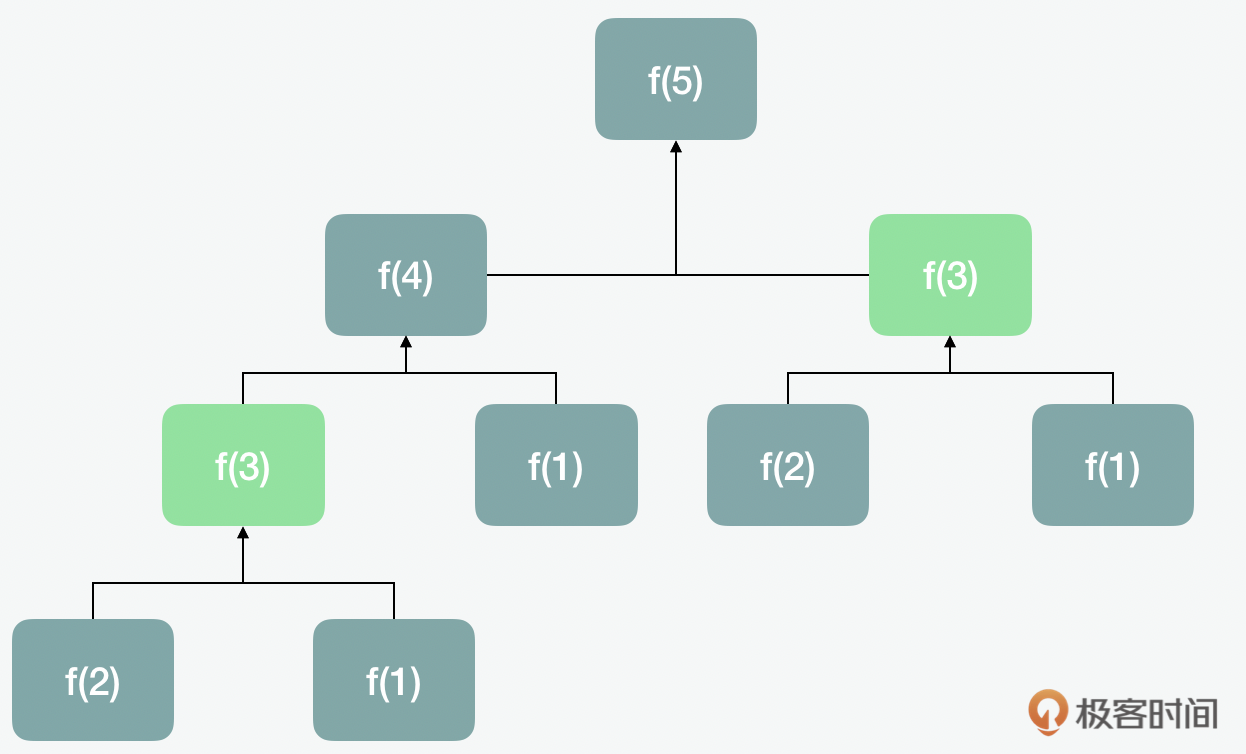
那么有没有什么办法,能够记住之前计算的结果,来避免这种重复的计算呢?
递归中的记忆函数
对了,我们可以利用上节课学到的作用域和闭包,在这里它又一次展示了它的强大。我们可以用闭包把递归函数中加入记忆(memoization)。在这里,fibonacci是一个递归,但是我们让它调用了一个外部的memo参数,这样一来memo就带有了“记忆”。我们可以用它来存储上一次计算的值,就可以避免重复计算了。所以记忆函数经常和递归结合起来使用。这里解决的重复计算问题,在算法中也被称为重叠子问题,而记忆函数就是一个备忘录。 function fibMemo(n, memo = [0, 1, 1]) { if (memo[n]) { return memo[n]; } // 递归+分治+闭包 memo[n] = fibMemo(n - 1, memo) + fibMemo(n - 2, memo); return memo[n]; } console.log(fibMemo(10)); // 55
递归中的尾递归
在上面的例子里,我们可以看到它的时间复杂度是(O(2^{n}))。那有没有办法能够把时间和空间复杂度都降低到(O(n))呢?这里面我们可以看看尾递归。尾递归的意思就是在函数的尾部执行递归的调用。通过用尾递归的方式,最多递归n次,因为在每次递归的过程中都会n-1。 function fibTailRecursive(n, lastlast, last){ if (n == 0) { return lastlast; } if (n == 1) { return last; } return fibTailRecursive(n-1, last, lastlast + last); } console.log(fibTailRecursive(10, 0, 1)); // 55
递归中的内存管理
在上一讲中,我们在了解闭包的原理的过程中也了解了函数调用栈的概念。在国外,有一个很有名的技术问答网站叫做stack overflow,翻译成中文就是栈溢出。在我们用递归的时候,如果没有很好的控制,就会遇到这个性能问题。所以下面,我们再来看看递归中的内存管理。
在前面的例子中,我们看到在用递归来代替迭代的方案中,虽然它的写法比迭代要简便,但付出的是性能上的代价。因为这是一个函数不断自己调用自己的过程,会占用大量栈的空间,所以除了时间复杂度,它会有较高的空间复杂度需要考虑。而且稍有不慎,当它不能停止被调用的时候,可能会引起栈溢出。
比如在前面乘阶的例子中,我们可以在调用栈(call stack)中看到函数每次被调用的过程。
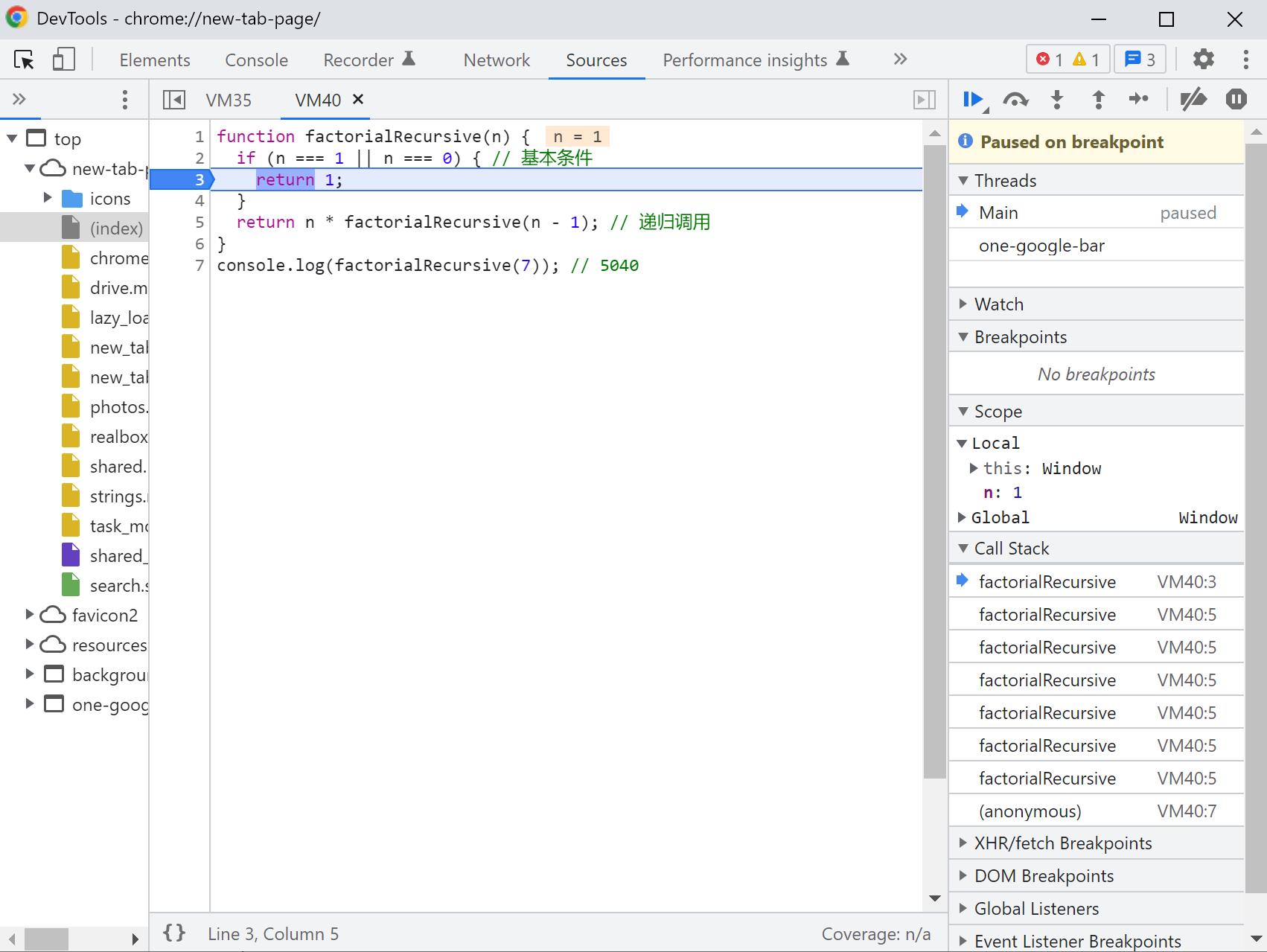
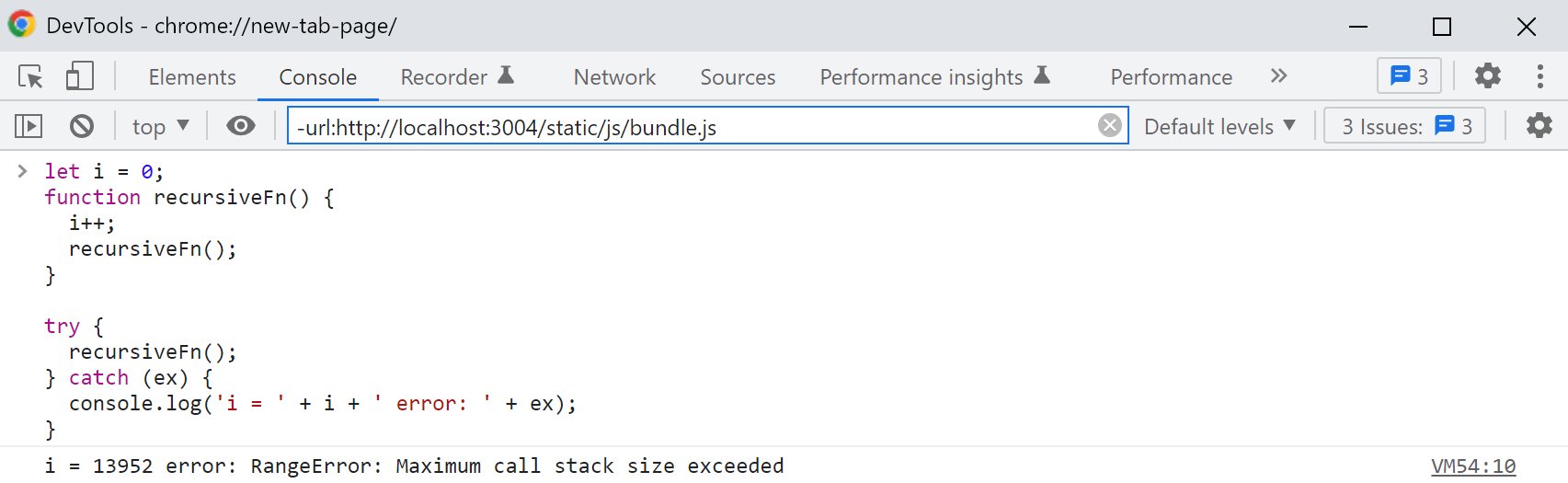
JavaScript从ES6版本的标准开始,定义了尾调用优化。里面提到,如果一个函数是一个函数里的最后一个动作,它会被当做跳转而不是子程序来处理。也就是说这个代码会不停地被重复,所以这也是为什么要有一个基本条件的重要性。在实际操作中,绝大多数浏览器都会自己定义一个防止栈溢出的限制,比如Chrome在下面的一个无限循环的例子中调用了13952次之后,就出现了一个超出最大栈范围的错误消息,并且停止了递归。 let i = 0; function recursiveFn() { i++; recursiveFn(); } try { recursiveFn(); } catch (ex) { console.log(‘i = ‘ + i + ‘ error: ‘ + ex); }
延伸:递归复杂度计算
在迭代中,Big-O的分析相对简单,因为循环可以清楚地定义什么时候增加、减少或者停止。但是在分析递归的时候,我们就需要分析两个部分了,一个是基础条件,一个是递归。所以在做递归的复杂度计算,通常会用到主定理(master theorem)。我们先来看看这个定理的组成部分。
在这里面,n是问题规模的大小,a是子问题个数,n/b是每个子问题的大小,(O(n^{c}))是将原问题分解和将子问题的解合并的时间。
[T(n) = aT(n/b)+O(n^{c})]
基于(c)和(log_{b}(a))的对比,会有三种结果。(log_{b}(a))代表了(aT(n/b)),即解决当前层问题所需要的时间复杂度;(c)代表了(O(n^{c})),即将原问题分解和将子问题的解合并的时间。
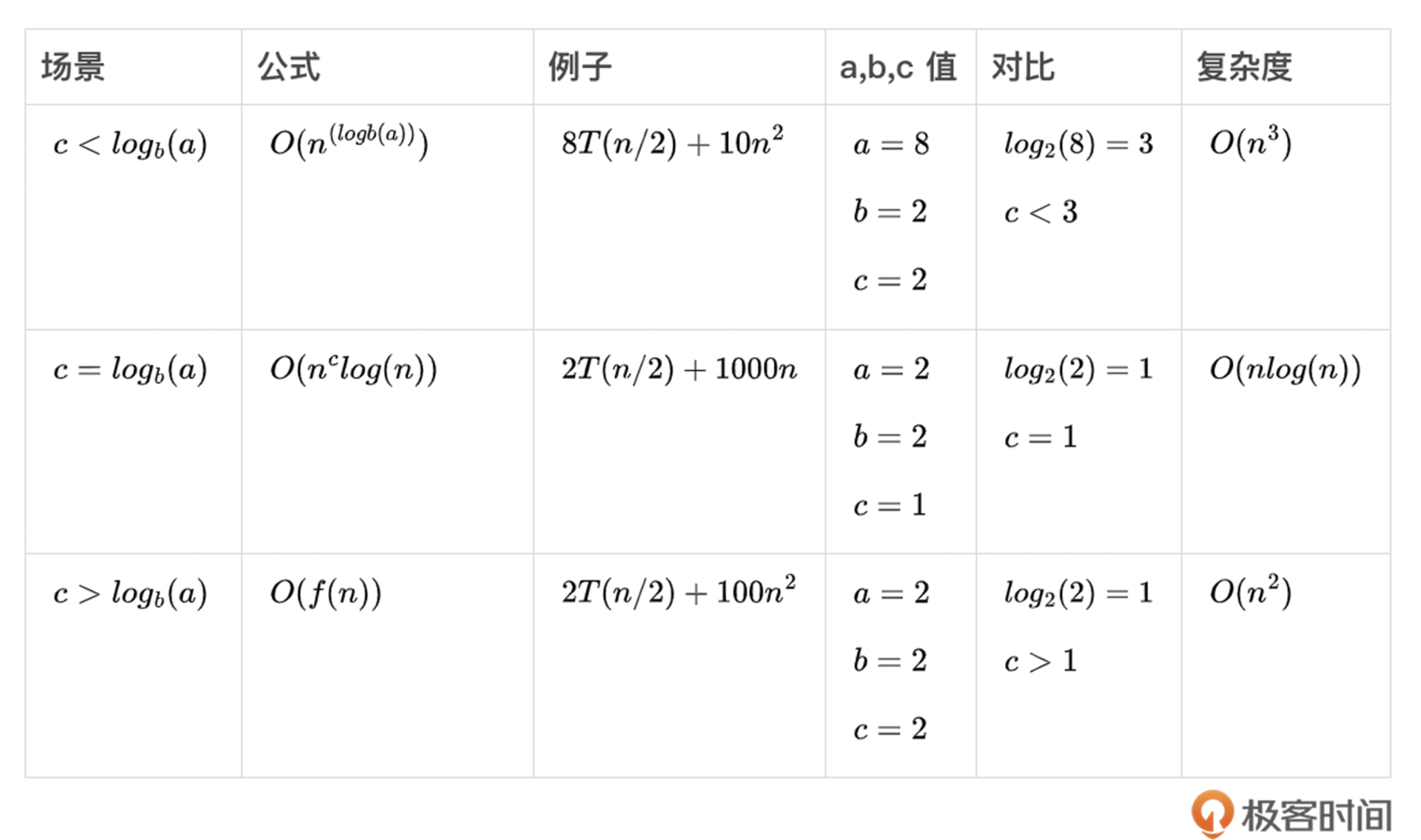
当然我们说并不是所有递归问题都符合主定理公式的形式,那么遇到这种问题该怎么办呢?在这种情况下,我们也可以尝试使用递推公式和递归树。
下面,我们先来看看使用递推公式的方式。递推公式可以帮助我们在写递归的时候,设计递归函数。同时,它还有另外一个作用就是计算复杂度。如果我们用递推公式来计算斐波那契的时间复杂度的话,要先提炼出它的递推公式及时间复杂度的推导过程。这里,你可以看到,每一次函数调用会产生两次额外的调用,计算呈指数级增加。 // 斐波那契递推公式 T (n) = T (n − 1) + T (n − 2) // 时间复杂度的推导 T(n) = T(n − 1) + T(n − 2) + O(1); T(n − 1) = T(n − 2) + T(n − 3) + O(1); T(n − 2) = T(n − 3) + T(n − 4) + O(1); // 每次指数级的增加 f(6) /* <– 一次 f(5) /* f(4) // f(3) //// f(2) //////// f(1) //////////////// <– 16 f(0) //////////////////////////////// <– 32
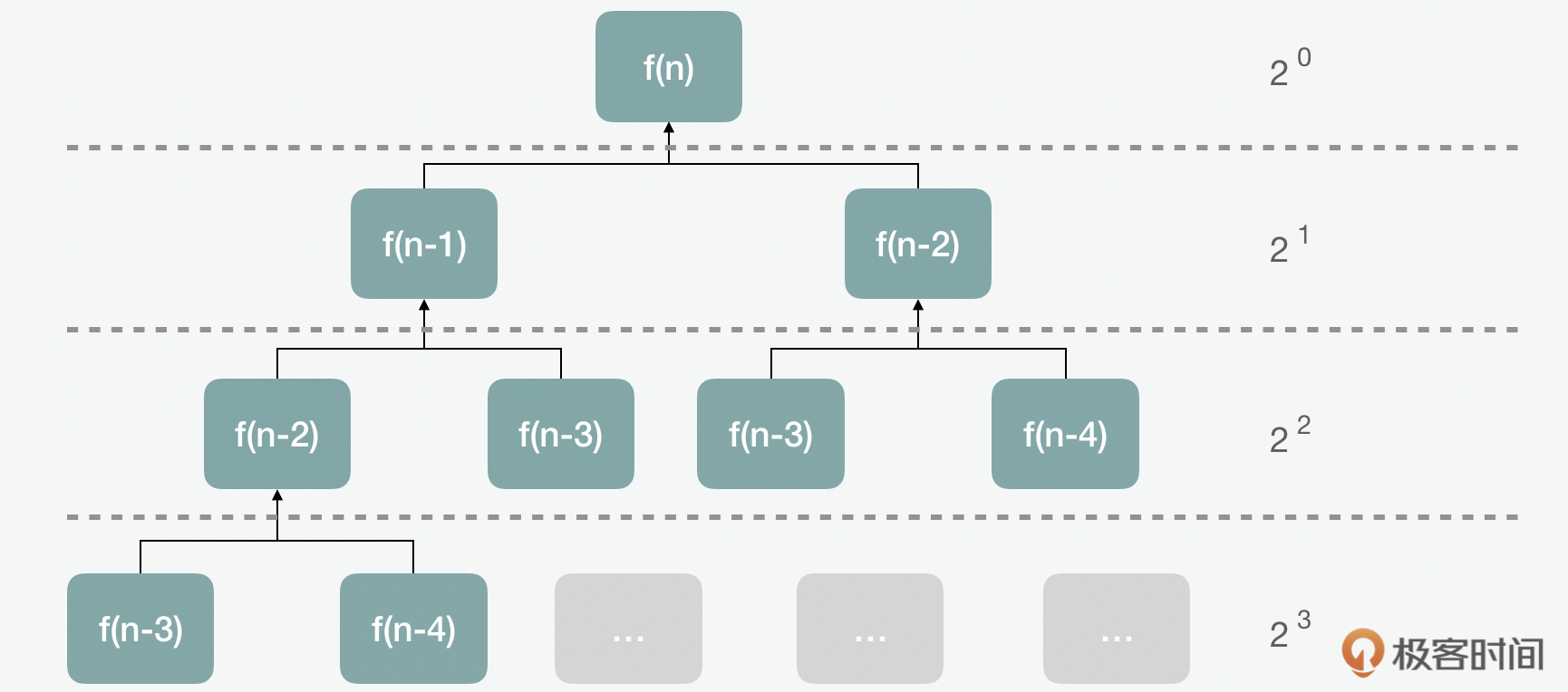
上面通过递推公式计算复杂度的方式还是很复杂的,那么还有没有更简单直观的计算方式呢?我们来看看递归树。递归树的方式,我们可以更直观地看出结果。这里当长路径为n的话,对应的耗时为(2^{n}-1),所以最高的时间复杂就是(2^{n})。
总结
这节课我们学习了算法中最核心的两种方法,迭代和递归。就和我们讲JavaScript编程范式的时候,讲到函数中的闭包和对象中的this一样,你会发现,我们后面讲到的80%算法都离不开它的影子。请记住这个二八定律,只要把迭代和递归的概念吃透搞明白,对算法的学习,可以说是有着事半功倍的效果。
如果要对比迭代和递归的话,从整体的性能来说,迭代是优于递归的。而如果从代码的整洁性来看,递归看起来更简洁。而且递归和作用域、闭包结合起来形成的记忆函数和尾递归,都能从一定程度上减少其“副作用”。下面我们就结合这张图,总结下针对这些副作用的解决方法吧。
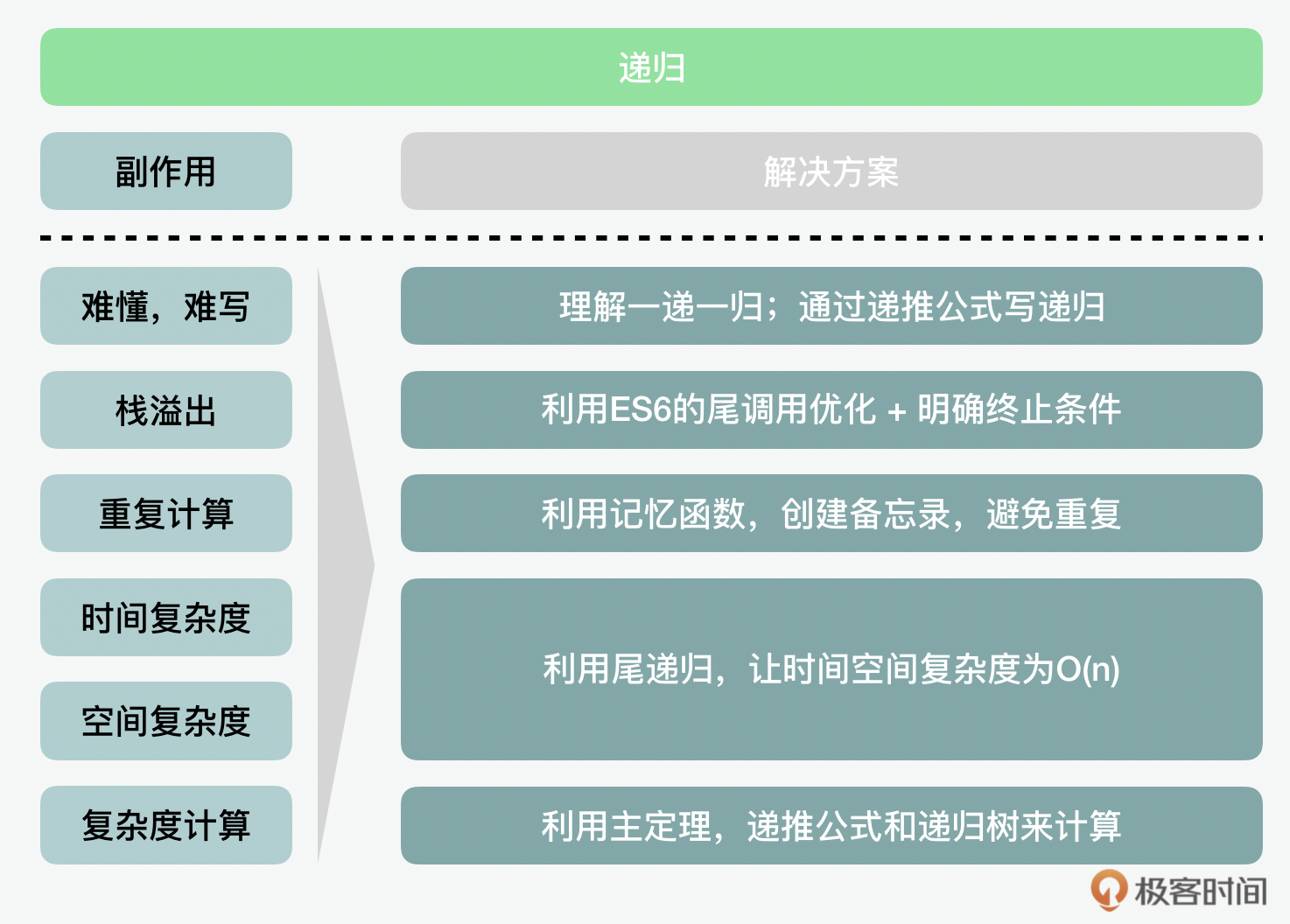
所以在算法中我们应该用迭代还是递归呢?这里同样没有绝对,应用上,你可以根据它们的优劣势,结合实际情况来应用。我个人认为,我们写的代码主要还是给人读的,而不是最终的机器码。所以我的建议是以代码的“简洁可读性”为先,然后再针对机器无法替我们优化的“副作用”的部分所产生的问题做手动的优化。
思考题
前面我们讲到了针对栈溢出的尾调用优化,你知道尾递归调用优化是如何实现的吗?
期待在留言区看到你的分享,我们一起交流讨论。另外,也欢迎你把今天的内容分享给更多的朋友。
参考资料
https://learn.lianglianglee.com/%e4%b8%93%e6%a0%8f/JavaScript%20%e8%bf%9b%e9%98%b6%e5%ae%9e%e6%88%98%e8%af%be/12%20JS%e8%af%ad%e4%b9%89%e5%88%86%e6%9e%90%e8%af%a5%e7%94%a8%e8%bf%ad%e4%bb%a3%e8%bf%98%e6%98%af%e9%80%92%e5%bd%92%ef%bc%9f.md
更多学习
更多实时资讯,前沿技术,生活趣事。尽在【老马啸西风】
交流社群:[交流群信息](https://mp.weixin.qq.com/s/rkSvXxiiLGjl3S-ZOZCr0Q)
