双数组实现原理

双数组Tire树是Tire树的升级版，Tire取自英文Retrieval中的一部分，即检索树，又称作字典树或者键树。

下面简单介绍一下Tire树。

1.1 Tire树

Trie是一种高效的索引方法，它实际上是一种确定有限自动机(DFA)，在树的结构中，每一个结点对应一个DFA状态，每一个从父结点指向子结点(有向)标记的边对应一个DFA转换。

遍历从根结点开始，然后从head到tail，由关键词(本想译成键字符串，感太别扭)的每个字符来决定下一个状态，标记有相同字符的边被选中做移动。

注意每次这种移动会从关键词中消耗一个字符并走向树的下一层，如果这个关键字符串空了，并且走到了叶子结点，那么我们达到了这个关键词的出口。

如果我们被困在了一点结点，比如因为没有分枝被标记为当前我们有的字符，或是因为关键字符串在中间结点就空了，这表示关键字符串没有被trie认出来。

图1.1.1即是一颗Tire树，其由字典{AC,ACE,ACFF,AD,CD,CF,ZQ}构成。

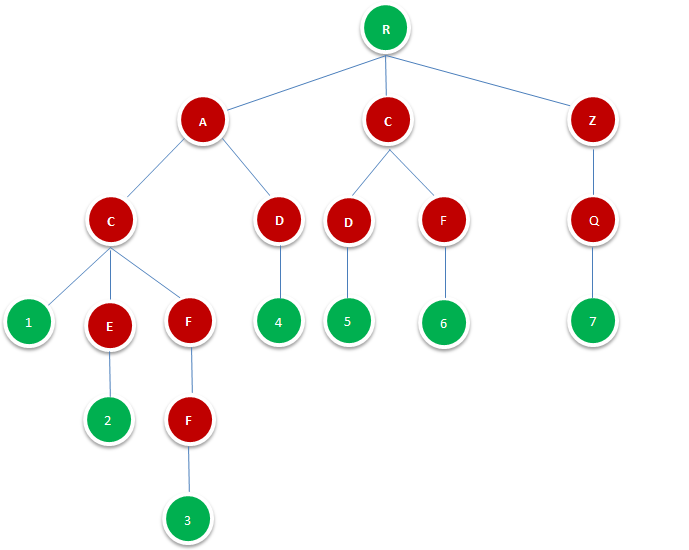
tire 树

图中R表示根节点，并不代表字符，除根节点外每一个节点都只包含一个字符。

从根节点到图中绿色节点，路径上经过的字符连接起来，为该节点对应的字符串。绿色叶节点的数字代表其在字典中的位置

1.2 Tire树的用途

Tire树核心思想是空间换取时间，利用字符串的公共前缀来节省查询时间，常用于统计与排序大量字符串。

其查询的时间复杂度是O（L），只与待查询串的长度相关。

所以其有广泛的应用，下边简单介绍下Tire树的用途

Tire用于统计：

题目：给你100000个长度不超过10的单词。对于每一个单词，我们要判断他出没出现过，如果出现了，求第一次出现在第几个位置。

解法：从第一个单词开始构造Tire树，Tire树包含两字段，字符与位置，对于非结尾字符，其位置标0，结尾字符，标注在100000个单词词表中的位置。对词表建造Tire树，对每个词检索到词尾，若词尾的数字字段>0,表示单词已经在之前出现过，否则建立结尾字符标志，下次出现即可得知其首次出现位置，便利词表即可依次计算出每个单词首次出现位置复杂度为O（N×L）L为最长单词长度，N为词表大小

Tire 用于排序

题目：对10000个英文名按字典顺序排序

解法：建造Tire树，先序便利即可得到结果。

1.3 针对Tire树的改进

Tire树虽然很完美，但缺点是空间的利用率很低，比如建立一颗ASCII的Tire树，每个节点的指针域为256，这样每个节点既有256个指针域，即使子节点置空，仍会有空间占用问题，解决办法是动态数组Tire树，即对子节点分配动态数组，生成子节点则动态扩大数组容量，这样便能有效的利用空间。

出于对Tire树占用空间的更有效利用，便引入了今天的主题：双数组Tire树，顾名思义，即把Tire树压缩到两个数组中。

双数组Tire树拥有Tire树的所有优点，而且刻服了Tire树浪费空间的不足，使其应用范围更加广泛，例如词法分析器，图书搜索，拼写检查，常用单词过滤器，自然语言处理中的字典构建等等。

在基于字典的分词方法中，许多开源的实现都采用了双数组Tire树。

2 构造双数组Tire树

下面进入本文的主题双数组Tire树，其基本观念是压缩trie树，使用两个一维数组BASE和CHECK来表示整个树。

双数组缺点在于：构造调整过程中，每个状态都依赖于其他状态，所以当在词典中插入或删除词语的时候，往往需要对双数组结构进行全局调整,灵活性能较差。

但对与，这个缺点是可以忽略的，因为核心词典已经预先建立好并且有序的，并且不会添加或删除新词，所以插入时不会产生冲突。

所以常用双数组Tire树来载入整个核心分词词典。

2.1 双数组的构造

Tire 树终究是一颗树形结构，树形结构的两个重要要素便是前驱和后继，把Tire树压缩到双数组中，只需要保持能查询到每个节点的前驱和后继即可。

Tire 树中几个重要的概念

STATE：状态，实际为在数组中的下标 
CODE： 状态转移值，实际为转移字符的 ASCII码
BASE： 表示后继节点的基地址的数组，叶子节点没有后继，标识为字符序列的结尾标志
CHECK：标识前驱节点的地址

什么是 Trie？

Trie 是一种数字搜索树。（有关数字搜索树的详细信息，请参阅 [Knuth1972]。） [Fredkin1960] 引入了 trie 术语，它是“Retrieval”的缩写。

trie

Trie 是一种高效的索引方法。它确实也是一种确定性有限自动机 (DFA)（例如，参见 [Cohen1990]，了解 DFA 的定义）。在树结构中，每个节点对应一个 DFA 状态，从父节点到子节点的每个（有向）标记边对应一个 DFA 转换。遍历从根节点开始。然后，从头到尾，一个接一个地取出密钥串中的字符，确定下一个要走的状态。选择标有相同字符的边进行行走。请注意，这种步行的每一步都会消耗键中的一个字符并沿着树向下走一步。如果密钥用尽并且到达叶节点，那么我们到达该密钥的出口。如果我们卡在某个节点上，要么是因为没有用我们拥有的当前字符标记的分支，要么是因为密钥在内部节点已用尽，那么它只是意味着该密钥未被 trie 识别。

请注意，从根遍历到叶子所需的时间不取决于数据库的大小，而是与密钥的长度成正比。因此，在一般情况下，它通常比 B-tree 或任何基于比较的索引方法快得多。它的时间复杂度与散列技术相当。

除了效率之外，trie 还提供了在密钥拼写错误的情况下搜索最近路径的灵活性。

例如，通过在行走时跳过键中的某个字符，我们可以修复插入类型的拼写错误。通过走向一个节点的所有直接子节点而不消耗键中的字符，我们可以修复删除拼写错误，甚至可以修复替换拼写错误，如果我们只是删除没有分支的关键字符并下降到所有直接子节点当前节点。

实现 Trie 需要什么？

通常，DFA 用一个转换表表示，其中行对应于状态，列对应于转换标签。然后，当输入等于标签时，保存在每个单元格中的数据将成为给定状态的下一个状态。

这是一种有效的遍历方法，因为每个转换都可以通过二维数组索引来计算。但是，在空间使用方面，这是相当奢侈的，因为在 trie 的情况下，大多数节点只有几个分支，大部分表格单元格都是空白的。

同时，更紧凑的方案是使用链表来存储每个状态的转换。但是由于线性搜索，这会导致访问速度变慢。

因此，已经设计出仍然允许快速访问的表压缩技术来解决该问题。

[Johnson1975]（也在 [Aho+1985] pp. 144-146 中解释）用四个数组表示 DFA，在 trie 的情况下可以简化为三个。转换表行以重叠方式分配，允许其他行使用空闲单元格。

[Aoe1989] 通过将阵列减少到两个，提出了对三阵列结构的改进。

三重数组特里

正如 [Aho+1985] pp. 144-146 中所解释的，可以使用四个线性数组来完成 DFA 压缩，即 default、base、next 和 check。

但是，在比词法分析器更简单的情况下，例如仅用于信息检索的 trie，可以省略默认数组。

因此，可以根据该方案使用三个数组来实现 trie。

结构

三元数组结构由以下部分组成：

base 根据。 base 中的每个元素对应于 trie 的一个节点。对于一个 trie 节点 s，base[s] 是转换表中节点 s 所在行的 next 和检查池（稍后解释）中的起始索引。

next 下一个。该数组与 check 配合，为 trie 转换表中的行分配稀疏向量提供了一个池。向量数据，即来自每个节点的转换向量，将存储在该数组中。

check 查看。该数组与下一个并行工作。它标志着下一个单元格的所有者。这允许将彼此相邻的单元分配给不同的 trie 节点。这意味着来自多个节点的转换的稀疏向量被允许重叠。

定义 1

对于以字符 c 作为输入的从状态 s 到 t 的转换，三元数组 trie 中保持的条件是：

check[base[s] + c] = s
next[base[s] + c] = t 

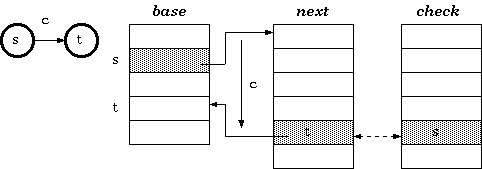
walking

根据定义 1，给定状态 s 和输入字符 c 的行走算法为：

t := base[s] + c;

  if check[t] = s then
      next state := next[t]
  else
      fail
  endif

Construction(建造)

要插入使字符 c 从状态 s 遍历到另一个状态 t 的转换，必须管理单元 next[base[s] + c]] 可用。

如果它已经空置，我们很幸运。

否则，必须重新定位单元当前所有者或状态 s 本身的整个转换向量。

每个案例的估计成本可以确定要移动哪一个。

在找到放置向量的空闲槽后，必须重新计算转换向量，如下所示。

假设新地点从 b 开始，搬迁过程为：

Procedure Relocate(s : state; b : base_index)
{ Move base for state s to a new place beginning at b }
begin
    foreach input character c for the state s
    { i.e. foreach c such that check[base[s] + c]] = s }
    begin
        check[b + c] := s;     { mark owner }
        next[b + c] := next[base[s] + c];     { copy data }
        check[base[s] + c] := none     { free the cell }
    end;
    base[s] := b
end

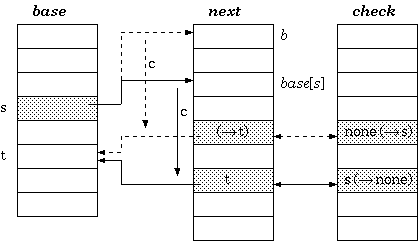
tripreloc

双数组 Trie

用于实现 trie 的三元组结构似乎定义良好，但保存在单个文件中仍然不切实际。

下一个/检查池可能能够保存在单个整数对数组中，但基本数组不会与池并行增长，因此通常是拆分的。

为了解决这个问题，[Aoe1989] 将结构简化为两个平行数组。

在双数组结构中，base 和 next 合并，结果只有两个平行数组，即 base 和 check。

结构

双数组 trie 中的节点直接链接到基本/检查池中，而不是像三数组 trie 中那样通过状态编号间接引用。

定义 2. 对于以字符 c 作为输入的从状态 s 到 t 的转换，在双数组 trie 中保持的条件是：

check[base[s] + c] = s
base[s] + c = t 

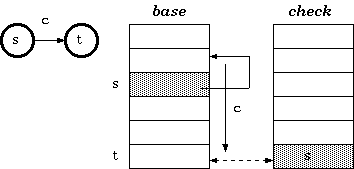
struct

walking 步行

根据定义 2，给定状态 s 和输入字符 c 的行走算法为：

t := base[s] + c;

  if check[t] = s then
      next state := t
  else
      fail
  endif

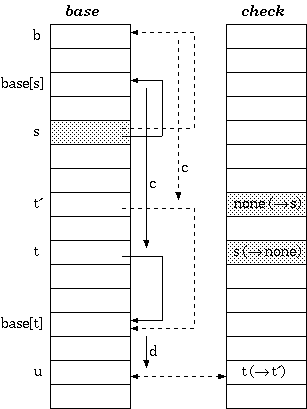
建造

double-array trie 的构造原则上与triple-array trie 的构造相同。不同之处在于基址重定位：

Procedure Relocate(s : state; b : base_index)
{ Move base for state s to a new place beginning at b }
begin
    foreach input character c for the state s
    { i.e. foreach c such that check[base[s] + c]] = s }
    begin
        check[b + c] := s;     { mark owner }
        base[b + c] := base[base[s] + c];     { copy data }
        { the node base[s] + c is to be moved to b + c;
          Hence, for any i for which check[i] = base[s] + c, update check[i] to b + c }
        foreach input character d for the node base[s] + c
        begin
            check[base[base[s] + c] + d] := b + c
        end;
        check[base[s] + c] := none     { free the cell }
    end;
    base[s] := b
end

doubreloc

后缀压缩

[Aoe1989] 还提出了一种存储压缩策略，通过将非分支后缀拆分为单个字符串存储，称为尾部，以便将其余非分支步骤减少为单纯的字符串比较。

对于两个独立的数据结构，双数组分支和后缀假脱机尾部，必须相应地修改键插入和删除算法。

key 插入

要插入一个新的key，可以用key一个字符一个字符遍历trie，直到卡住为止，找到分支位置。

没有分支可以去的状态就是插入新边的地方，由失败的字符标记。

但是，对于分支尾结构，插入点可以在分支中，也可以在尾部。

1.当分支点在双数组结构时

假设新key为字符串a1a2…ah-1ahah+1…an，其中a1a2…ah-1从根遍历trie到双数组结构中的节点sr，有没有边缘标记 ah 超出 sr。

[Aoe1989] 中称为 A_INSERT 的算法如下：

从 sr，将标记为 ah 的边插入到新节点 st；
让 st 成为指向尾池中字符串 ah+1...an 的单独节点。

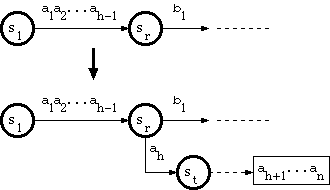
A-INSERT

2.当分支点在尾池时

由于通过尾串的路径没有分支，因此只对应一个键，假设尾对应的键是

a1a2…ah-1ah…ah+k-1b1…bm,

其中 a1a2…ah-1 为双数组结构，ah…ah+k-1b1…bm 在尾部。假设子串 a1a2…ah-1 从根遍历 trie 到节点 sr。

并假设新密钥的形式为

a1a2…ah-1ah…ah+k-1ah+k…an,

其中 ah+k <> b1。

[Aoe1989] 中称为 B_INSERT 的算法如下：

从 sr 开始，插入 ah...ah+k-1 的直线路径，在新节点 st 处结束；
从 st 开始，将标记为 b1 的边插入到新节点 su；
设 su 是指向尾池中字符串 b2...bm 的单独节点；
从 st 开始，将标记为 ah+k 的边插入到新节点 sv；
让 sv 是指向尾池中的字符串 ah+k+1...an 的单独节点。

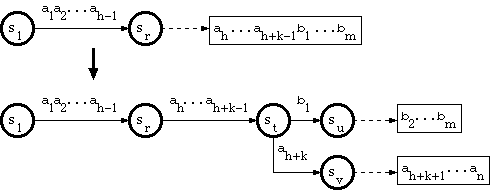
B-insert

key 删除

要从 trie 中删除一个 key，我们需要做的就是删除该 key 占用的尾块，以及所有专属于该 key 的双数组节点，而不涉及任何属于其他 key 的节点。

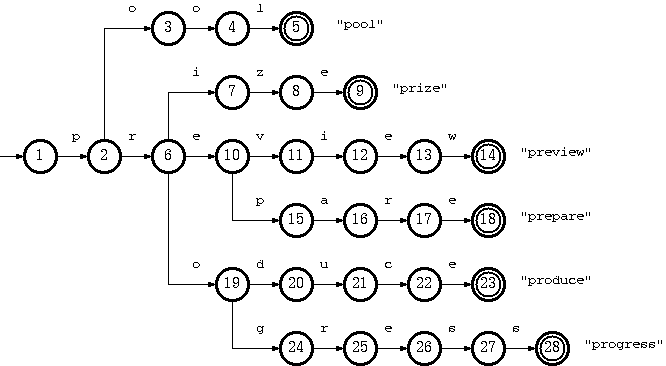
考虑一个接受语言 K = {pool#, prepare#, preview#, prize#, produce#, producer#, progress#} 的 trie：

key

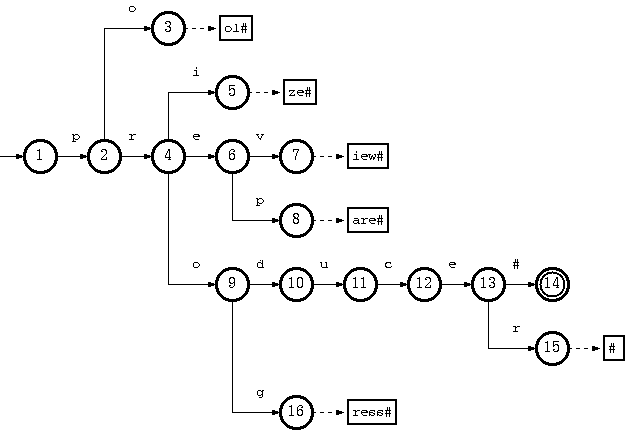
可以通过从尾池中删除尾部字符串“ol#”以及从双数组结构中删除节点 3 来删除键“pool#”。这是最简单的情况。

要删除键“produce#”，从双数组结构中删除节点 14 就足够了。但是生成的 trie 不会违反双数组结构中的每个节点，除了指向尾块的单独节点之外，都必须属于多个键的约定。从节点 10 开始的路径将仅属于密钥“producer#”。

但是违反这条规则并没有什么坏处。唯一的缺点是 trie 的不紧凑性。遍历、插入和删除算法是完整的。因此，为了删除算法的简单和高效，这应该放宽。

否则，如果任何节点需要从双数组结构移动到尾池，则必须有额外的步骤来检查同一子树中的其他键（“producer#”用于删除“produce#”）。

进一步假设已经删除了“produce#”（仅删除节点 14），我们还需要从 trie 中删除“producer#”。我们要做的是从tail中删除字符串“#”，并从双数组结构中删除节点15、13、12、11、10（现在只属于键“producer#”）。

由此我们可以总结出删除key k = a1a2…ah-1ah…an的算法，其中a1a2…ah-1是双数组结构，ah…an是尾池，如下：

Let sr := the node reached by a1a2...ah-1;
Delete ah...an from tail;
s := sr;
repeat
    p := parent of s;
    Delete node s from double-array structure;
    s := p
until s = root or outdegree(s) > 0.

其中 outdegree(s) 是 s 的子节点数。

双阵列池分配

为节点插入新分支时，新分支的数组元素可能已分配给另一个节点。在这种情况下，需要搬迁。

然后，效率关键部分变成了寻找新地方。蛮力算法沿着检查数组迭代以找到一个空单元格来放置第一个分支，然后确保所有其他分支也有空单元格。

因此，所用时间与双数组池的大小和字母表的大小成正比。

假设 trie 中有 n 个节点，字母表的大小为 m。双数组结构的大小为 n + cm，其中 c 是一个取决于 trie 特性的系数。蛮力算法的时间复杂度为 O(nm + cm2)。

[Aoe1989]提出了双数组结构中的空闲空间列表，使时间复杂度与trie的大小无关，而只取决于空闲单元的数量。

空闲单元格的检查数组被重新定义以保持指向下一个空闲单元格的指针（称为 G-link）：

定义 3. 设 r1, r2, … , rcm 为双数组结构中的空闲单元，按位置排序。

G-link定义如下：

check[0] = -r1
check[ri] = -ri+1 ; 1 <= i <= cm-1
check[rcm] = -1 

根据这个定义，否定检查意味着与普通算法中的“无”检查相同的意义。

这种编码方案形成了一个自由单元的单链表。

搜索空单元格时，仅访问 cm 空闲单元格，而不是像蛮力算法中的所有 n + cm 单元格。

但是，这仍然可以改进。

请注意，对于那些带有否定检查的单元格，相应的碱基没有给出任何定义。

因此，在我们的实现中，Aoe 的 G-link 被修改为双向链表，让每个空闲单元的基指向前一个空闲单元。

这可以加快插入和删除过程。

而且，为了方便引用列表头和尾，我们让列表是循环的。

第零个节点专用于列表的入口点。

trie 的根节点将从第一个单元格开始。

定义 4. 令 r1, r2, … , rcm 为双数组结构中的空闲单元，按位置排序。 G-link定义如下：

check[0] = -r1
check[ri] = -ri+1 ; 1 <= i <= cm-1
check[rcm] = 0
base[0] = -rcm
base[r1] = 0
base[ri+1] = -ri ; 1 <= i <= cm-1 

然后，搜索具有输入符号集 P = {c1, c2, …, cp} 的节点的槽只需要迭代具有否定检查的单元格：

{find least free cell s such that s > c1}
s := -check[0];
while s <> 0 and s <= c1 do
    s := -check[s]
end;
if s = 0 then return FAIL;  {or reserve some additional space}

{continue searching for the row, given that s matches c1}
while s <> 0 do
    i := 2;
    while i <= p and check[s + ci - c1] < 0 do
        i := i + 1
    end;
    if i = p + 1 then return s - c1;  {all cells required are free, so return it}
    s := -check[s]
end;
return FAIL;  {or reserve some additional space}

空闲时隙搜索的时间复杂度降低到 O(cm^2)。重定位阶段需要 O(m^2)。

因此，总时间复杂度为 O(cm^2 + m^2) = O(cm^2)。

保持空闲列表按位置排序很有用，这样通过数组的访问就变得更加有序。

当 trie 存储在磁盘文件或虚拟内存中时，这将是有益的，因为磁盘缓存或页面交换将被更有效地使用。因此，免费单元重用应保持此策略：

t := -check[0];
while check[t] <> 0 and t < s do
    t := -check[t]
end;
{t now points to the cell after s' place}
check[s] := -t;
check[-base[t]] := -s;
base[s] := base[t];
base[t] := -s;

因此，释放一个单元的时间复杂度为 O(cm)。

一个实现

在我的实现中，我在设计 API 时考虑了持久数据。尝试可以保存到磁盘并加载以供以后使用。在较新的版本中，非持久性使用也是可能的。您可以在内存中创建一个 trie，向其中填充数据、使用它并释放它，而无需任何磁盘 I/O。或者，您可以从磁盘加载 trie 并随时将其保存到磁盘。

trie 数据可跨平台移植。磁盘中的字节顺序始终是 little-endian，并且在 little-endian 或 big-endian 系统上都能正确读取。

Trie 索引是 32 位有符号整数。这允许在 trie 数据中总共有 2,147,483,646 (231 - 2) 个节点，这对于大多数问题域来说应该足够了。

每个数据条目都可以存储一个与之关联的 32 位整数值。此值可用于任何目的，取决于您的需要。

如果您不需要使用它，只需存储一些虚拟值即可。

对于稀疏数据的紧凑性，trie 字母集应该是连续的，但在一般字符集中通常不是这种情况。因此，在中间创建了输入字符和为 trie 设置的低级字母表之间的映射。

创建 trie 时，您必须通过在 .abm（字母映射）文件中列出其连续的字符代码范围来定义输入字符集。

然后，每个字符将被自动分配连续值的内部代码。

https://github.com/digitalstain/DoubleArrayTrie

参考资料