向量时钟
向量时钟(Vector Clock)是一种在分布式环境中为各种操作或事件产生偏序值的技术,它可以检测操作或事件的并行冲突,用来保持系统的一致性。
向量时钟方法在分布式系统中用于保证操作的有序性和数据的一致性。
向量时钟通常可以被认为是一组来自不同节点的时钟值Vi[1]、Vi[2]、…、Vi[n]。
在分布式环境中,第i个节点维护某一数据的时钟时,根据这些值可以知道其他节点或副本的状态,例如Vi[0]是第i个节点所了解的第0个节点上的时钟值,而Vi[n]是第i个节点所了解的第n个节点上的时钟值。
时钟值代表了节点上数据的版本信息,该值可以是来自节点本地时间的时间戳或者是根据某一规则生成有序数字。
例子
以3副本系统为例,该系统包含节点0、节点1和节点2。
某一时刻的状态可由表2-3来表示。
- 向量时钟实例
| / | V0 | V1 | V2 |
| V0 | 4 | 2 | 0 |
| V1 | 1 | 4 | 0 |
| V2 | 0 | 0 | 1 |
该表表示当前时刻各节点的向量时钟为:
节点0:V0(4,2,0)
节点1:V1(1,4,0)
节点2:V2(0,0,1)
在表2-3中,Vi代表第i个节点上的时钟信息,Vi[j]表示第i个节点所了解的第j个节点的时钟信息。
以第2行为例,该行为V1节点的向量时钟(1,4,0),其中”1”表示V1节点所了解的V0节点上的时钟值;”0”表示V1节点所了解的V2节点上的时钟值;”4”表示V1节点自身所维护的时钟值。
运维规则
下面具体描述向量时钟在分布式系统中的运维规则。
- 规则1:
初始时,我们将每个节点的值设置为0。每当有数据更新发生,该节点所维护的时钟值将增长一定的步数d,d的值通常由系统提前设置好。
该规则表明,如果操作a在操作b之前完成,那么a的向量时钟值大于b向量时钟值。
向量时钟根据以下两个规则进行更新。
- 规则2:
在节点i的数据更新之前,我们对节点i所维护的向量Vi进行更新:
Vi[i]= Vi[i]+d(d > 0)
该规则表明,当Vi[i]处理事件时,其所维护的向量时钟对应的自身数据版本的时钟值将进行更新。
- 规则3:
当节点i向节点j发送更新消息时,将携带自身所了解的其他节点的向量时钟信息。
节点j将根据接收到的向量与自身所了解的向量时钟信息进行比对,然后进行更新:
Vj[k] = max{Vi[k], Vj[k]}
在合并时,节点j的向量时钟每一维的值取节点i与节点j向量时钟该维度值的较大者。
两个向量时钟是否存在偏序关系,通过以下规则进行比较:
对于n维向量来说,Vi > Vj,如果任意k(0≤k≤n 1)均有Vi[k] > Vj[k]。
如果Vi既不大于Vj且Vj也不大于Vi,这说明在并行操作中发生了冲突,这时需要采用冲突解决方法进行处理,比如合并。
如上所示,向量时钟主要用来解决不同副本更新操作所产生的数据一致性问题,副本并不保留客户的向量时钟,但客户有时需要保存所交互数据的向量时钟。
如在单调读一致性模型中,用户需要保存上次读取到的数据的向量时钟,下次读取到的数据所维护的向量时钟则要求比上一个向量时钟大(即比较新的数据)。
优势
相对于其他方法,向量时钟的主要优势在于:
-
节点之间不需要同步时钟,即不需要全局时钟。
-
不需要在所有节点上存储、维护一段数据的版本数。
缺点
该方法的主要缺点就是向量时钟值的大小与参与的用户有关,在分布式系统中参与的用户很多,随着时间的推移,向量时钟值会增长到很大。
一些系统中为向量时钟记录时间戳,某一时间根据记录的时间对向量时钟值进行裁剪,删除最早记录的字段。
向量时钟在实现中有两个主要问题:如何确定持有向量时钟值的用户,如何防止向量时钟值随着时间不断增长。
实际例子
下面我们通过一个例子来体会向量时钟如何维护数据版本的一致性。
A、B、C、D 四个人计划下周去爬长城。
A首先提议周三去,此时B给D发邮件建议周四去,他俩通过邮件联系后决定周四去比较好。
之后C与D通电话后决定周二去。
然后,A询问B、C、D三人是否同意周三去,C回复说已经商量好了周二去,而B则回复已经决定周四去,D又联系不上,这时A得到不同的回复。
最新导致的混乱
如果他们决定以最新的决定为准,而A、B、C没有记录商量的时间,因此无法确定什么时候去爬长城。
向量时钟版本
下面我们使用向量时钟来”保证数据的一致性”:为每个决定附带一个向量时钟值,并通过时钟值的更新来维护数据的版本。
在本例中我们设置步长d的值为1,初始值为0。
(1)在初始状态下,将四个人(四个节点)根据规则1将自身所维护的向量时钟清零,如下所示:
A(0,0,0,0)
B(0,0,0,0)
C(0,0,0,0)
D(0,0,0,0)
(2)A提议周三出去
A首先根据规则2对自身所维护的时钟值进行更新,同时将该向量时钟发往其他节点。
B、C、D节点在接收到A所发来的时钟向量后发现它们所知晓的A节点向量时钟版本已经过时,因此同样进行更新。
更新后的向量时钟状态如下所示:
A(1,0,0,0)
B(1,0,0,0)
C(1,0,0,0)
D(1,0,0,0)
(3)B和D通过邮件进行协商
B 觉得周四去比较好,那么此时B首先根据规则2更新向量时钟版本(B(1,1,0,0)),然后将向量时钟信息发送给D(D(1,0,0,0))。
D通过与B进行版本比对,发现B的数据较新,那么D根据规则3对向量时钟更新,如下所示。
A(1,0,0,0)
B(1,1,0,0)
C(1,0,0,0)
D(1,1,0,0)
4)C 和 D 进行电话协商
C 觉得周二去比较好,那么此时C首先更新自身向量时钟版本(C(1, 0, 1, 0)),然后打电话通知D(D(1, 1, 0, 0))。
D根据规则3对向量时钟进行更新。
此时系统的向量时钟如下所示:
A(1,0,0,0)
B(1,1,0,0)
C(1,0,1,0)
D(1,1,1,0)
最终,通过对各个节点的向量时钟进行比对,发现D的向量时钟与其他节点相比具有偏序关系。
因此该系统将决定”周二”一起去爬山。
版本冲突
该方法中数据版本可能出现冲突,即不能确定向量时钟的偏序关系。
假如C在决定周三爬山后并没有将该决定告诉其他人,那么系统在此刻将不能确定某一数据向量时钟的绝对偏序关系。
比较简单的冲突解决方案是随机选择一个数据的版本返回给用户。
而在 Dynamo 中系统将数据的不一致性冲突交给客户端来解决。
当用户查询某一数据的最新版本时,若发生数据冲突,系统将把所有版本的数据返回给客户端,交由客户端进行处理。
其他策略
其实没有一个比较好的解决冲突的版本:就笔者目前所了解,加上时间戳算是一个策略。
具体方法是再加一个维度信息:数据更新的时间戳(timestamp)。
[A:1, B:2,C:4,ts:123434354] ,如果发生冲突,再比较一下两个数据的ts,大的数值说明比较后更新,选择它作为最终数据。
并对向量时钟进行订正。
算法的本质
why
为什么这种算法就可以做到传统算法做不到的事情呢?
虽然我们已经学会了怎么使用时钟向量算法,但是似乎还和算法的本质隔着一层雾:
我们其实并没有解决“不同节点之间统一的时钟”这一个客观的问题,但是通过向量时钟算法,我们却可以确定一些更改的先后顺序,而这些是在之前无法确定。
那多出来的信息是从哪里获得的?
vs 传统算法
结合前面给出的两张图中的两个例子,对比传统的方法和时间向量算法的差异:
其实客观上是可以得知 B 对 Key 的更改是在 A 之后的,因为 B 是在收到 A 的更改之后才进行的下一步更改。
传统的方法丢失了这部分信息,而向量时钟算法将这个信息保存了起来,用于后面对更改的先后顺序的判定。
用数学表达就是:
因为 TB0 > TA1, TB1 > TB0,所以 TB1 > TA1;
而传统的方法丢失了“TB1 > TB0”这条信息。
那么,既然向量时钟的唯一目的是传输“TB1 > TB0”这条信息,那么其他任何方法,只要能够将这类信息包含进去,也拥有和向量时钟算法相同的效果。
比如 Git 中冲突合并的思想和向量时钟算法的本质其实是一样的:Git 中不同的本地仓库拥有不同的时间维度,每一次 commit 对应一个时间维度上值的增加,可以快速合并的两个仓库对应的时间向量是具有偏序关系的。
总结如下:
给不同的节点设置不同的时间维度体现了不同节点之间没有一个统一的时钟,因此不同节点之间的时间就不具有可比性;
每个节点的更新会在自己的时间维度上加 1 体现了同一个节点上的时间是可以比较的;
时钟向量 A,B 具有偏序关系且 A>B 体现了 A 是在同一节点上,在 B 的基础上增加的得到的;同一节点上发生的事件可以判断先后顺序,那么可以得知 A 发生在 B 之后;
时钟向量 A,B 不具有偏序关系 体现了 A,B 之间不存在能够将某一个向量的尾端顺着同一个节点连到另一个向量中间的事件;
实质
所以向量时钟算法的实质是:
(1)将逻辑上可以合并的冲突成功合并;
(2)逻辑上无法合并的冲突依旧冲突;
拓展:和狭义相对论时空观念的比较
上面算法中的这种 不同节点中的时间不具有不具有可比性 和 用一个多维的时间来代替一维的时间 的时空观,和狭义相对论中的时空观非常类似。
在狭义相对论中,同一事件从不同的惯性参考系中观察是不一样的,而两次事件可以建立因果关系的前提是:两个事件之间可以用等于或小于光速的速度传递信息(或者说一事件位于另一事件的光锥内部)。
联系:
| 在狭义相对论中的描述 | 在向量时钟算法中的描述 |
|---|---|
| 不同的惯性参考系有不同的时间 | 不同的节点有不同的时钟向量维度 |
| 两件事件具有因果关系(事件 2 位于事件 1 的光锥内部) | 两次更改可确定先后顺序(两个向量具有偏序,类似光锥内部) |
| 两件事件不具有因果关系(事件 2 位于事件 1 的光锥外部) | 两件事件不具有因果关系(事件 2 位于事件 1 的光锥外部) |
区别:
狭义相对论可以用洛伦兹变换将不同的参考系中的时间进行变换(利用到不同参考系之间的相对速度),
但是向量时钟算法不可以(其实逻辑上也可以,但是实现后没有现实意义),所以只能用多维的时间来表征不同节点中的时间却没法相互转化。
向量时钟的空间无限增长问题
以上的做法还比较完美的解决了问题,这里只列举了四个决策者的向量时钟,不过在现实生活中,如果有很多的决策者,相当于有很多的客户端,整个向量时钟的长度就无限制增长了,这对于存储系统来说,不是一个好消息。
我们需要想办法解决。
一个直接的想法是,不要用client来标识向量空间,用server来标识向量空间,因为server的数量是可控的,
这里用X,Y两台server来重现以上决策的过程,只是标签不再用客户端,而是用server标识,决策过程如下
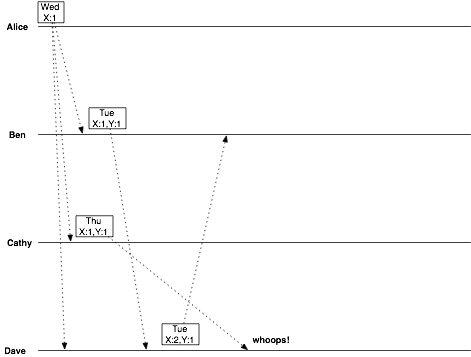
此时Dave收到两个消息
Tue X:2,Y:1 with Ben
Thu X:1,Y1 from Cathy (这个消息比较新)
发现后者是前者的祖先,所以自然抛弃祖先,最终最新的,这样就悄无声息的把Cathy给他的消息给丢了。
所以尝试用server来做标识,以期减少向量时钟的空间是不可取的,因为会丢数据。
实际情况还是需要用客户端的标识来做向量时钟。
向量时钟的剪枝
所以为了解决向量时钟空间的无限增长问题,引入了向量时钟的剪枝。
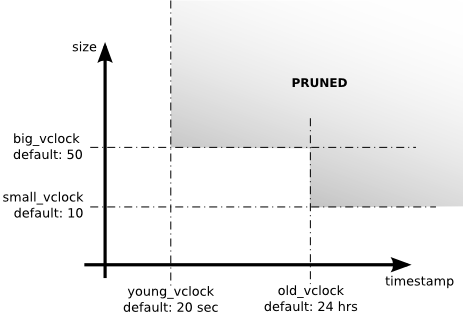
Riak用四个参数来避免向量时钟空间的无限增长:
small_vclock
big_vclock
young_vclock
old_vclock
small_vclock 和 big_vclock参数标识向量时钟的长度,如果长度小于small_vclock就不会被剪枝掉,如果长度大于big_vclock就会被剪枝掉
young_vclock和old_vclock参数标识存储这个向量时钟时的时间戳,剪枝策略同理,大于old_vclock的才会被剪枝掉,剪枝策略如下图
这样只会丢掉一些向量时钟的信息,即数据更新过程的信息,但是不会丢掉实实在在的数据。
只有当一种情况会有问题,就是一个客户端保持了一个很久之前的向量时钟,然后继承于这个向量时钟提交了一个数据,此时就会有冲突,因为服务器这边已经没有这个很久之前的向量时钟信息了,已经被剪枝掉了可能,所以客户端提交的此次数据,在服务端无法找到一个祖先,此时就会创建一个sibling。
所以这个剪枝的策略是一个权衡tradeoff,一方面是无限增长的向量时钟的空间,另一方面是偶尔的会有”false merge”,对,但肯定的是,不会悄无声息的丢数据。
综上,为了防止向量时钟空间的无限增长,剪枝还是比用server标识向量时钟工作的更好。
个人收获
感觉 git 的代码分支合并应该也有类似的思想。
这个作者可以联系到相对论,很有趣。
