1、FIFO(先进先出)算法

FIFO是类似队列的算法，如果空间满了需要加入新数据先进入缓存的数据会被优先被淘汰。

淘汰过程：

FIFO

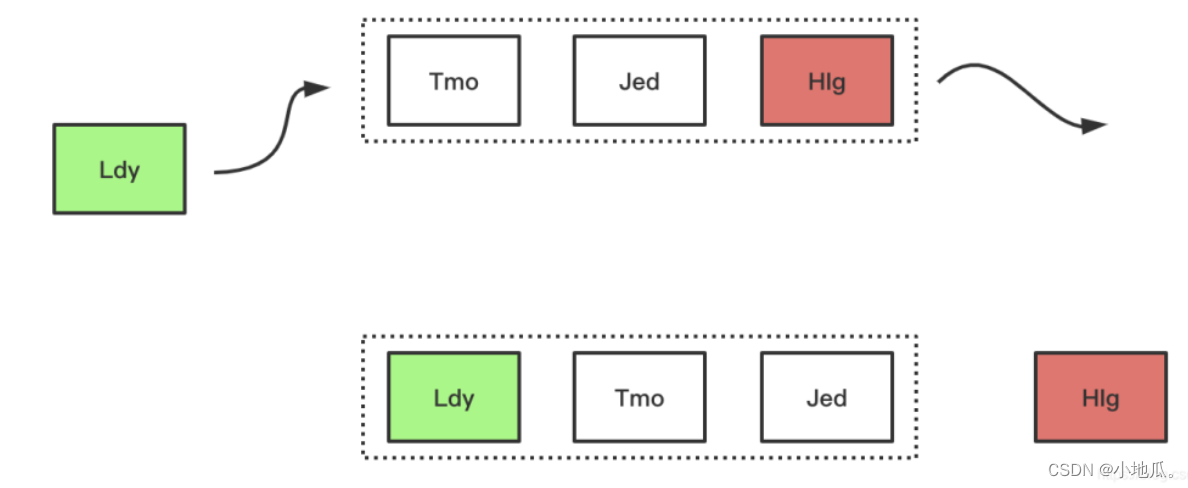
优点：最简单，最公平的一种数据淘汰算法，逻辑简单，易于实现。

缺点：缓存命中率低。

2、LRU(最近最久未使用)算法

如果空间用尽需要加入新数据会优先淘汰最久未被访问(访问少的在未来被访问的概率也是最低的)的数据。

LRU是以时间先后顺序来衡量要淘汰的数据。适用于局部突发流量场景。

淘汰过程：

LRU

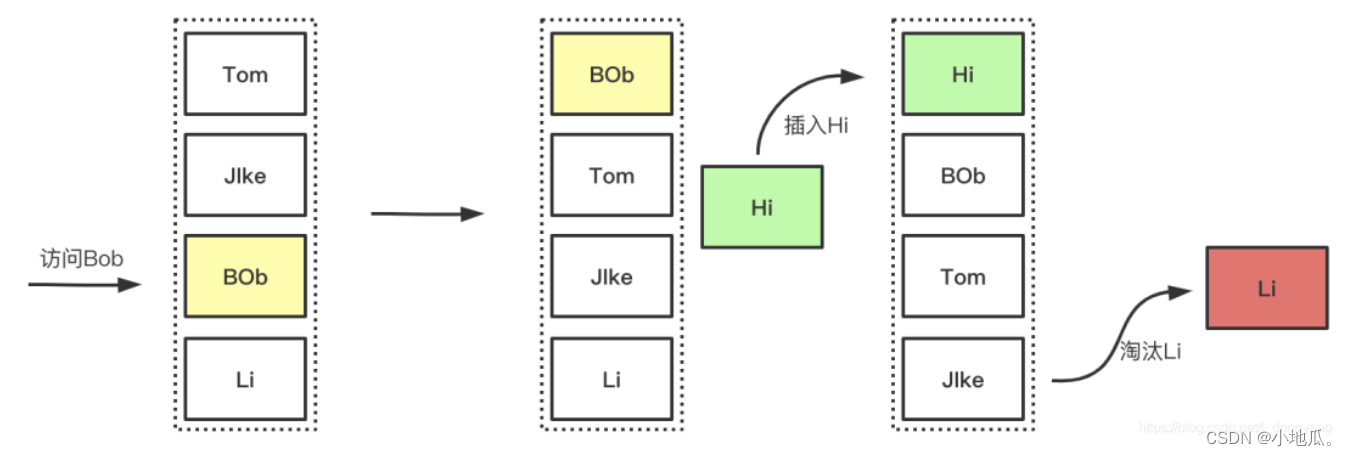
优点：

实现简单，一般情况下会有很好的命中率，比较常用。
有效的对访问比较频繁的数据进行保护，提高热点数据的命中率。
局部突发流量场景，对突发性的稀疏流量(n个1，n个2，突然来了1个3，3就属于突然稀疏流量)表现很好。

缺点：

在存在周期性(比如12345，12345的访问)的局部热点数据场景，空间满了会导致周期性的局部热点数据被淘汰。不能很好的处理偶发性，周期性的数据，影响命中率。

3、LFU(最近最少使用)算法

如果空间用尽需要加入新数据会优先淘汰时间段内访问次数最低(访问次数少的在未来被使用的概率也很小)的数据。

LFU是以时间段内的使用次数衡量淘汰的数据。适用于局部周期性流量场景。

淘汰过程：插入数据满了，优先淘汰在一定时间间隔内的访问频率最低的元素。

LFU

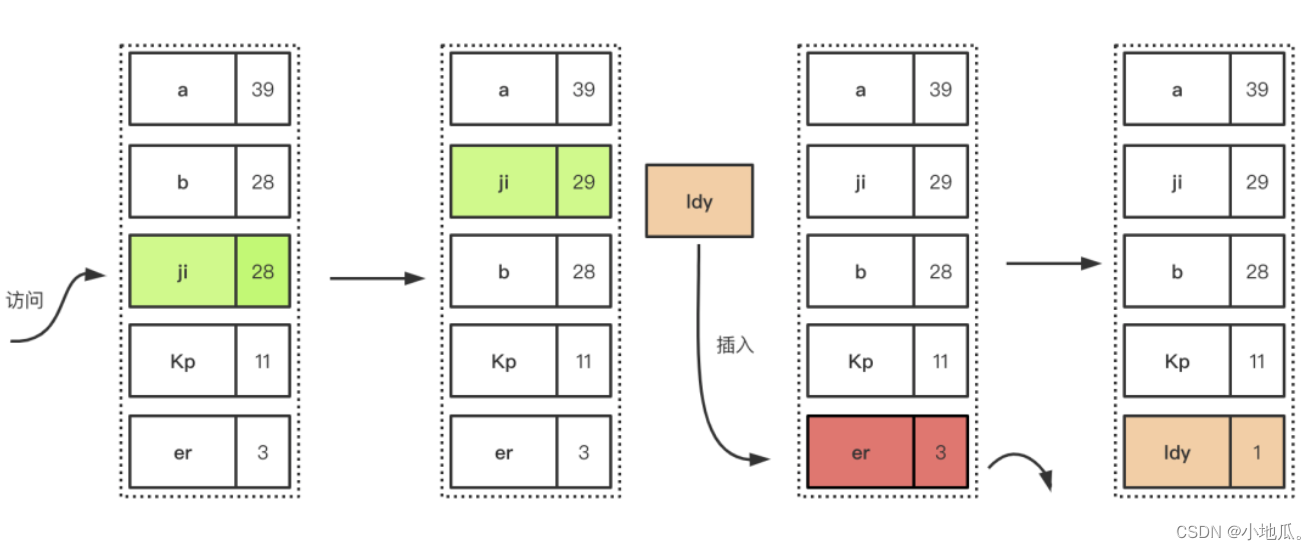
优点：

LFU适用于局部周期性的场景，有很好的命中率。
在局部周期性流量场景下，LFU是以次数为基准，能准确的保证和提高命中率。

缺点：

需要记录数据的访问频次，需要额外的空间开销。
需要给每个记录项维护频率信息，每次访问都需要更新，增加时间开销。
对突发性的稀疏流量场景下，算法命中率会下降。原因：LFU针对访问次数的大小淘汰，前期访问的数据，累计次数很大，新来的缓存数据累加时间短。

老的记录占用缓存，过去的一些大量被访问的记录，在之后不一定会继续使用，一直占用位置。突发的稀疏流量，很容易被淘汰。导致缓存命中率下降。

4、TinyLFU 算法

TinyLFU是为了解决LFU上面的三个缺点而设计出来的。

(1)减少访问频率的存储的空间开销和访问记录更新的时间开销采用Count–Min Sketch 算法。

Count–Min Sketch算法类似布隆过滤器，基于概率统计，存储访问频率，节省空间。

工作原理：

1.某个key计算出4个hash函数，落在不同的位置，每当元素被访问时针对hash计算找到对应的位置，将进行次数加1。

2.查询某个key的频率，需要取得4个索引位置的频率信息，取4个位置中的最小值返回。

实现方案：

实现方案

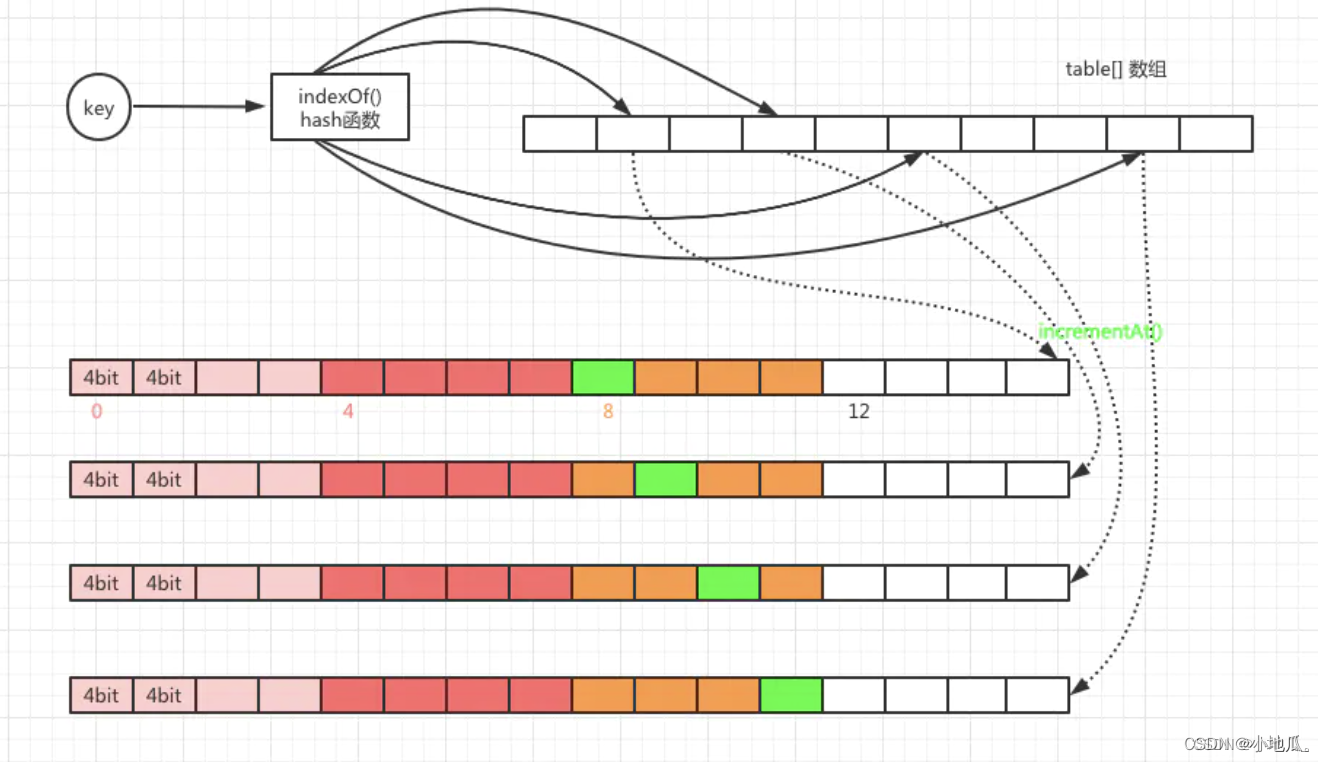
节约空间开销方式：默认访问频次最高15次(15次就算是热点数据了)，用4位就可以存储15。一个long类型64位置，每个long分成16份4位。一个key对应4个hash值，一个long就可以存储4个key的访问次数。一个long类型数组大小就是容量的4倍。节约了4分之3的空间。

(2)提升对局部热点数据的算法命中率，使用保鲜机制，尽量让缓存保持相对”新鲜”，访问越大越不新鲜，适当降低保证新鲜度。

Caffeine有一个新鲜度机制，剔除掉过去频率很高，之后不经常使用的缓存。具体操作就是整体的统计计数(所有key的频率统计和的最大值)达到某一个取值时，所有记录的频率统计除以2。

TinyLFU 的算法流程：缓存空间不够时，TinyLFU找到要淘汰的元素(频率最小的元素)，新元素放入缓存，替代要淘汰的元素。

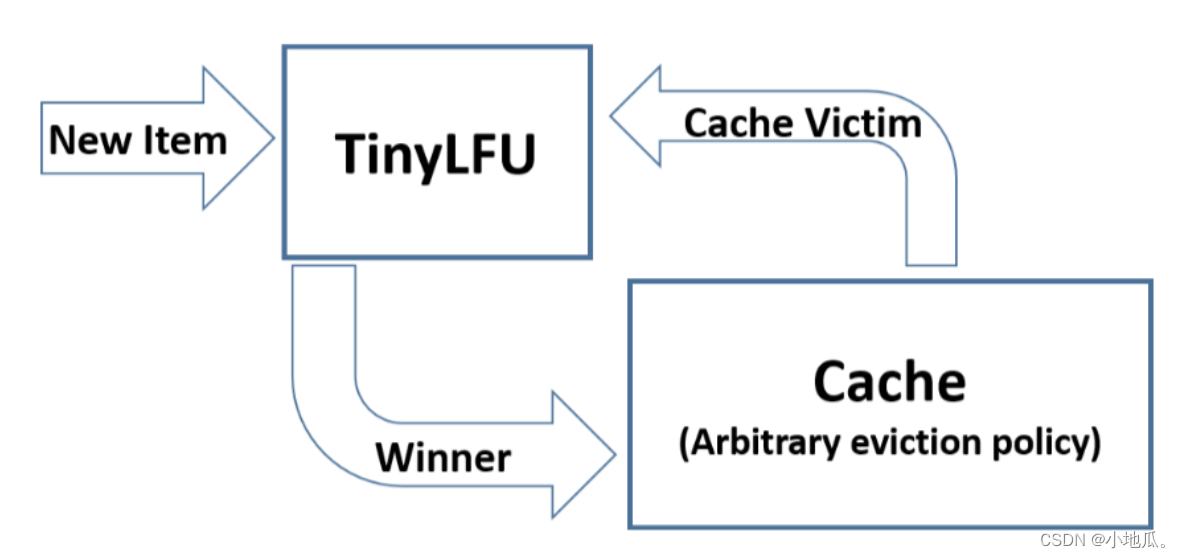
TinyLFU 的算法流程

5、W-TinyLFU 算法

TinyLFU在面对突发性的稀疏流量变现比较差，因为新的记录还没有建立足够多的频率就被淘汰了，导致命中率下降。

W-TinyLFU是对TinyLFU的一个优化，加入了LRU应对局部突发流量，实现缓存命中率最优。

W-TinyLFU= LRU(适合局部突发流量)+LFU(适合局部周期流量)。

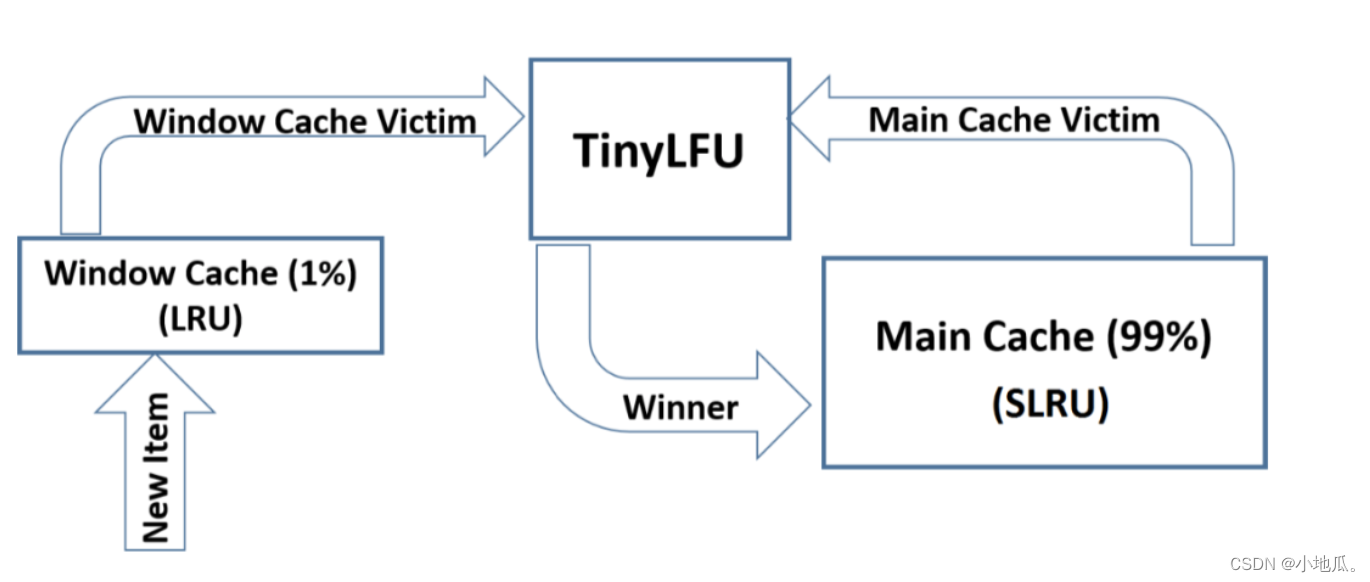
W-TinyLFU

W-TinyLFU将缓存分为2大区域：window cache(应对局部突发流量) 和 main cache(应对局部周期流量)。main cache又拆分成Protected Cache（保护区）和Probation Cache（考察区）两个区域，这两个区域都是基于LRU的Cache。Caffeine的默认比例：LRU(1%)，剩下99%中protected(80%)，probation(20%)。这时整体性能和命中率表现得最好(已经过实验验证)。

在运行时可以根据统计数据（statistics）去动态调整。

W-TinyLFU算法写入流程：新的缓存项写入缓存，先写入window cache区，如果window cache区满了，根据LRU把淘汰出来的数据放到Probation(考察)区域。如果Probation区满了，与probation中通过lru淘汰的数据进行使用TinyLFU pk。

胜者留在Probation区域，输者被淘汰。Probation中的数据被访问了，则移动到Protected。如果Protected满了，protected根据LRU淘汰到probation。

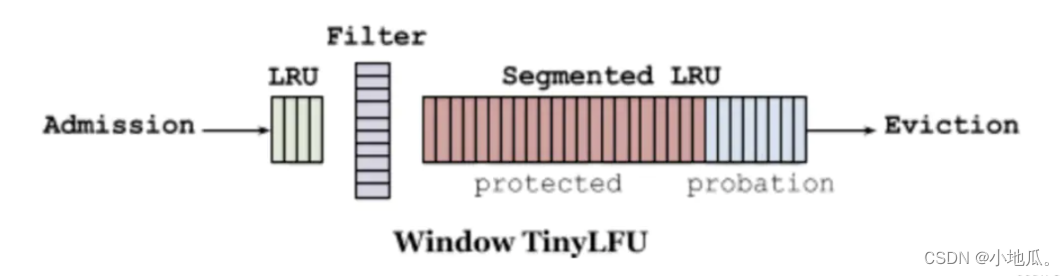
W-TinyLFU

优点：

使用Count-Min Sketch算法存储访问频率，极大的节省空间。
TinyLFU会定期进行新鲜度提升、访问次数的衰减操作，应对访问模式变化。
使用W-LRU机制能够提高缓存命中率。

四、Caffeine 代码实现

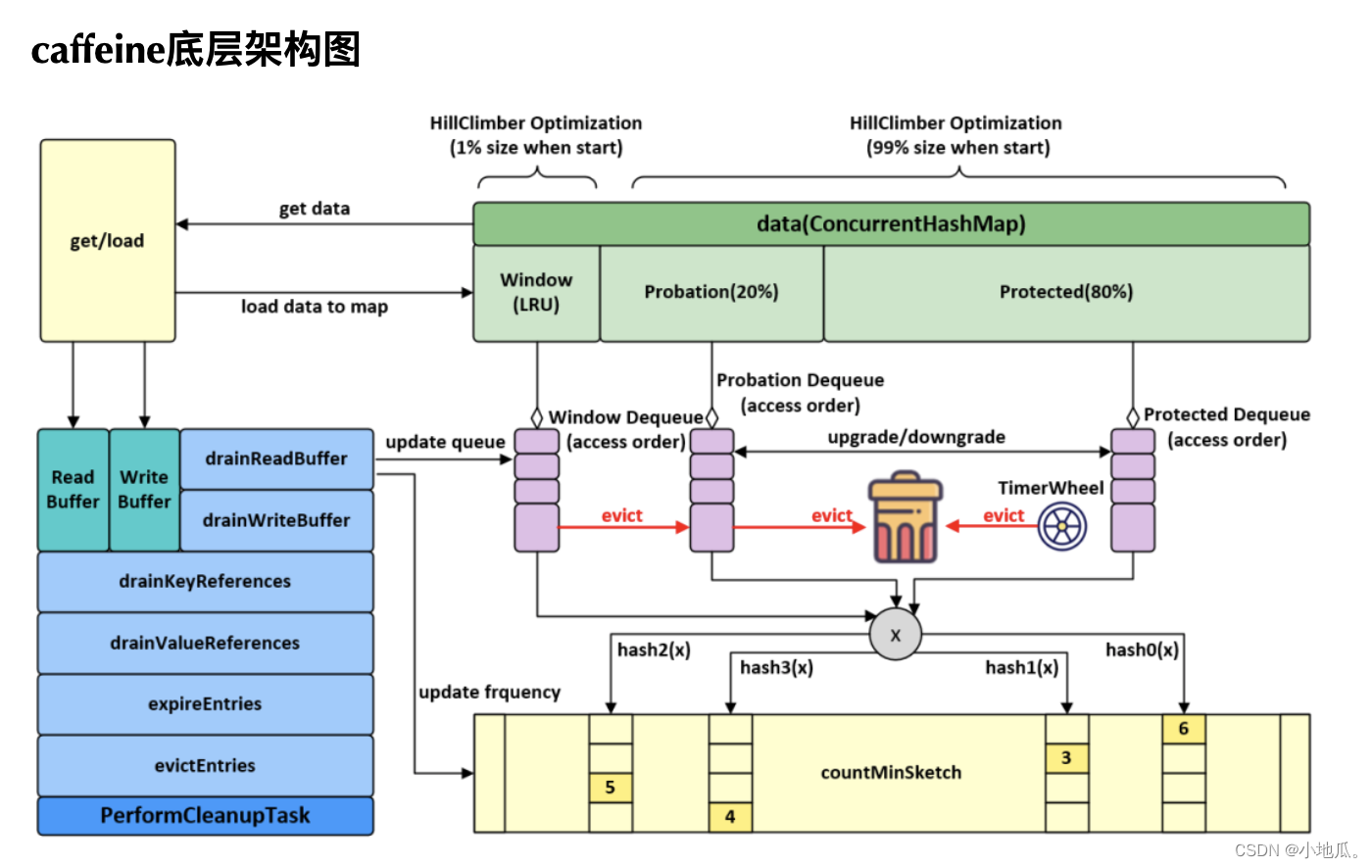
Caffeine 架构图

缓存操作执行流程：

通过put操作将数据放入data属性中（ConcurrentHashMap）。
创建AddTask任务，放入(offer)写缓存：writeBuffer。
从writeBuffer中获取任务并执行其run方法,追加记录频率：代码实现在frequencySketch().increment(key)。
往window区写入数据。
如果数据超过window区大小，将数据移到probation区。
比较从window区晋升的数据和probation区的老数据的频率，输者被淘汰，从data中删除。

相关代码：

1.Count–Min Sketch算法写入频率和查询频率和保新机制代码实现：

//1.Count–Min Sketch 算法 写入频率 使用FrequencySketch.increment(key)方法实现：
public void increment(@NonNull E e) {
    if (!this.isNotInitialized()) {
        //根据key的hashCode通过一个哈希函数得到一个hash值
        int hash = this.spread(e.hashCode());
        //Caffeine把64long分成16份，4bit一份，start是定位到具体的份的位置。
        //用hash值低两位作为随机数，左移2位，得到小于16的值
        //start 值：0、4、8、12
        int start = (hash & 3) << 2;
        //indexOf根据hash取获得四个元素在table数组下标的index，
        int index0 = this.indexOf(hash, 0);
        int index1 = this.indexOf(hash, 1);
        int index2 = this.indexOf(hash, 2);
        int index3 = this.indexOf(hash, 3);
        //根据index和start(+1, +2, +3)的值，把table[index]对应的等分追加1
        boolean added = this.incrementAt(index0, start);
        added |= this.incrementAt(index1, start + 1);
        added |= this.incrementAt(index2, start + 2);
        added |= this.incrementAt(index3, start + 3);
        //key的访问次数是否达到有个最大值
        //size为key的访问次数之合。sampleSize为最大值。size每统计一次+1
        if (added && ++this.size == this.sampleSize) {
            this.reset();
        }
    }
}
int indexOf(int item, int i) {
    long hash = ((long)item + SEED[i]) * SEED[i];
    hash += hash >>> 32;
    return (int)hash & this.tableMask;
}
//j表示16等分的下标，index对应等分的位置
boolean incrementAt(int i, int j) {
    //offset当于在64位中的下标 16 * 4
    int offset = j << 2;
    //统计数最大为15
    long mask = 15L << offset;
    //如果结果不等于15 就追加1，等于15就不追加。
    if ((this.table[i] & mask) != mask) {
        long[] var10000 = this.table;
        var10000[i] += 1L << offset;
        return true;
    } else {
        return false;
    }
}
 
//2.查询某个key的访问次数
@NonNegative
public int frequency(@NonNull E e) {
    if (this.isNotInitialized()) {
        return 0;
    } else {
        int hash = this.spread(e.hashCode());
        //得到下标
        int start = (hash & 3) << 2;
        int frequency = 2147483647;
        //循环四次，分别获取在table数组中不同的下标位置
        for(int i = 0; i < 4; ++i) {
            int index = this.indexOf(hash, i);
            //定位到table[index] + 等分的位置，再根据mask取出计数值
            int count = (int)(this.table[index] >>> (start + i << 2) & 15L);
            //取四个中的较小值
            frequency = Math.min(frequency, count);
        }
        return frequency;
    }
}
 
//3.保新机制代码实现
void reset() {
    int count = 0;
    for(int i = 0; i < this.table.length; ++i) {
        count += Long.bitCount(this.table[i] & 1229782938247303441L);
        this.table[i] = this.table[i] >>> 1 & 8608480567731124087L;
    }
    this.size = (this.size >>> 1) - (count >>> 2);
}

2.evictEntries()淘汰方法入口：

//最大的个数限制
long maximum;
//当前的个数
long weightedSize;
//window区的最大限制
long windowMaximum;
//window区当前的个数
long windowWeightedSize;
//protected区的最大限制
long mainProtectedMaximum;
//protected区当前的个数
long mainProtectedWeightedSize;
 
//1.window区的LRU queue 缓存1%的数据
@GuardedBy("evictionLock")
protected AccessOrderDeque<Node<K, V>> accessOrderWindowDeque() {
  throw new UnsupportedOperationException();
}
//probation区的LRU queue 缓存main内数据的20%
@GuardedBy("evictionLock")
protected AccessOrderDeque<Node<K, V>> accessOrderProbationDeque() {
  throw new UnsupportedOperationException();
}
//protected区的LRU queue 缓存main内数据的80%
@GuardedBy("evictionLock")
protected AccessOrderDeque<Node<K, V>> accessOrderProtectedDeque() {
  throw new UnsupportedOperationException();
}
 
//淘汰方法入口
@GuardedBy("evictionLock")
void evictEntries() {
    if (!evicts()) {
      return;
    }
    // 淘汰window区的记录
    //candidate  第一个 准备从Window区晋升的元素
    int candidates = evictFromWindow();
    //淘汰Main区的记录
    evictFromMain(candidates);
}
//新数据直接到窗口缓存区，超过Window区大小，需要进入到probation区
//使用LRU淘汰
@GuardedBy("evictionLock")
int evictFromWindow() {
    int candidates = 0;
    Node next;
    //判断头节点，是否超过区域最大限制，超过限制需要和probation区要淘汰的数据进行pk
    for(Node node = (Node)this.accessOrderWindowDeque().peek(); this.windowWeightedSize() > this.windowMaximum() && node != null; node = next) {
        next = node.getNextInAccessOrder();
        if (node.getPolicyWeight() != 0) {
            node.makeMainProbation();
            //window区删除node
            this.accessOrderWindowDeque().remove(node);
            //node移动到probation区
            this.accessOrderProbationDeque().add(node);
            ++candidates;
            this.setWindowWeightedSize(this.windowWeightedSize() - (long)node.getPolicyWeight());
        }
    }
    return candidates;
}
  
//主缓存取 数据进入probation队列后，如果超过最大容量，需要淘汰数据
@GuardedBy("evictionLock")
void evictFromMain(int candidates) {
    int victimQueue = 1;
    //victim是probation queue的头部
    Node<K, V> victim = (Node)this.accessOrderProbationDeque().peekFirst();
    //candidate是probation queue的尾部（刚晋升过来的数据）
    Node candidate = (Node)this.accessOrderProbationDeque().peekLast();
    //当缓存容量不够时需要处理
    while(this.weightedSize() > this.maximum()) {
        if (candidates == 0) {
            candidate = null;
        }
        if (candidate == null && victim == null) {
            if (victimQueue == 1) {
                victim = (Node)this.accessOrderProtectedDeque().peekFirst();
                victimQueue = 2;
            } else {
                if (victimQueue != 2) {
                    break;
                }
  
                victim = (Node)this.accessOrderWindowDeque().peekFirst();
                victimQueue = 0;
            }
        } else if (victim != null && victim.getPolicyWeight() == 0) {
            victim = victim.getNextInAccessOrder();
        } else if (candidate != null && candidate.getPolicyWeight() == 0) {
            candidate = candidate.getPreviousInAccessOrder();
            --candidates;
        } else {
            Node evict;
            if (victim == null) {
                evict = candidate.getPreviousInAccessOrder();
                Node<K, V> evict = candidate;
                candidate = evict;
                --candidates;
                this.evictEntry(evict, RemovalCause.SIZE, 0L);
            } else if (candidate == null) {
                evict = victim;
                victim = victim.getNextInAccessOrder();
                this.evictEntry(evict, RemovalCause.SIZE, 0L);
            } else {
                K victimKey = victim.getKey();
                K candidateKey = candidate.getKey();
                Node evict;
                if (victimKey == null) {
                    evict = victim;
                    victim = victim.getNextInAccessOrder();
                    this.evictEntry(evict, RemovalCause.COLLECTED, 0L);
                } else if (candidateKey == null) {
                    --candidates;
                    evict = candidate;
                    candidate = candidate.getPreviousInAccessOrder();
                    this.evictEntry(evict, RemovalCause.COLLECTED, 0L);
                } else if ((long)candidate.getPolicyWeight() > this.maximum()) {
                    //节点超过最大个数限制直接淘汰
                    --candidates;
                    evict = candidate;
                    candidate = candidate.getPreviousInAccessOrder();
                    this.evictEntry(evict, RemovalCause.SIZE, 0L);
                } else {
                    --candidates;
                    //根据数据victimKey和candidateKey访问频率比较，失败的淘汰
                    if (this.admit(candidateKey, victimKey)) {
                        //candidateKey胜出，淘汰victimKey
                        evict = victim;
                        victim = victim.getNextInAccessOrder();
                        this.evictEntry(evict, RemovalCause.SIZE, 0L);
                        candidate = candidate.getPreviousInAccessOrder();
                    } else {
                        //victimKey胜出，淘汰candidateKey
                        evict = candidate;
                        candidate = candidate.getPreviousInAccessOrder();
                        this.evictEntry(evict, RemovalCause.SIZE, 0L);
                    }
                }
            }
        }
    }
}
 
//在window队列通过lru淘汰出来的"候选者candidate"与
//probation队列通过lru淘汰出来的"被驱逐者victim"进行频率比较，失败者将被从cache中真正移除。
@GuardedBy("evictionLock")
boolean admit(K candidateKey, K victimKey) {
    int victimFreq = this.frequencySketch().frequency(victimKey);
    int candidateFreq = this.frequencySketch().frequency(candidateKey);
    //频率高获胜
    if (candidateFreq > victimFreq) {
        return true;
    } else if (candidateFreq <= 5) {
        return false;
    } else {
        //随机淘汰 (为了防止hash冲突攻击)
        int random = ThreadLocalRandom.current().nextInt();
        return (random & 127) == 0;
    }
}
 
//probation区域的数据移动到protected区域过程
//当数据被访问时并且该数据在probation中，这个数据就会移动到protected中去，
//同时通过lru从protected中淘汰一个数据进入到probation中
/** Promote the node from probation to protected on an access. */
@GuardedBy("evictionLock")
void reorderProbation(Node<K, V> node) {
  if (!accessOrderProbationDeque().contains(node)) {
    // Ignore stale accesses for an entry that is no longer present
    return;
  } else if (node.getPolicyWeight() > mainProtectedMaximum()) {
    return;
  }
  // If the protected space exceeds its maximum, the LRU items are demoted to the probation space.
  // This is deferred to the adaption phase at the end of the maintenance cycle.
  setMainProtectedWeightedSize(mainProtectedWeightedSize() + node.getPolicyWeight());
  accessOrderProbationDeque().remove(node);
  accessOrderProtectedDeque().add(node);
  node.makeMainProtected();
}

3.动态调整window区和protected区的大小 climb()方法：

//与上次命中率之差的阈值
static final double HILL_CLIMBER_RESTART_THRESHOLD = 0.05d;
//步长（调整）的大小（跟最大值maximum的比例）
static final double HILL_CLIMBER_STEP_PERCENT = 0.0625d;
//步长的衰减比例
static final double HILL_CLIMBER_STEP_DECAY_RATE = 0.98d;
  /** Adapts the eviction policy to towards the optimal recency / frequency configuration. */
//climb方法的主要作用就是动态调整window区的大小（相应的，main区的大小也会发生变化，两个之和为100%）。
//因为区域的大小发生了变化，那么区域内的数据也可能需要发生相应的移动。
@GuardedBy("evictionLock")
void climb() {
  if (!evicts()) {
    return;
  }
  //确定window需要调整的大小
  determineAdjustment();
  //如果protected区有溢出，把溢出部分移动到probation区。因为下面的操作有可能需要调整到protected区。
  demoteFromMainProtected();
  long amount = adjustment();
  if (amount == 0) {
    return;
  } else if (amount > 0) {
    //增加window的大小
    increaseWindow();
  } else {
    //减少window的大小
    decreaseWindow();
  }
}
 
@GuardedBy("evictionLock")
void determineAdjustment() {
  //如果frequencySketch还没初始化，则返回
  if (frequencySketch().isNotInitialized()) {
    setPreviousSampleHitRate(0.0);
    setMissesInSample(0);
    setHitsInSample(0);
    return;
  }
  //总请求量 = 命中 + miss
  int requestCount = hitsInSample() + missesInSample();
  //默认下sampleSize = 10 * maximum。没达到最大值返回。
  if (requestCount < frequencySketch().sampleSize) {
    return;
  }
  //命中率的公式 = 命中 / 总请求
  double hitRate = (double) hitsInSample() / requestCount;
  //命中率的差值
  double hitRateChange = hitRate - previousSampleHitRate();
  //本次调整的大小，是由命中率的差值和上次的stepSize决定的
  double amount = (hitRateChange >= 0) ? stepSize() : -stepSize();
  //下次的调整大小：如果命中率的之差大于0.05，则重置为0.065 * maximum，否则按照0.98来进行衰减
  double nextStepSize = (Math.abs(hitRateChange) >= HILL_CLIMBER_RESTART_THRESHOLD)
      ? HILL_CLIMBER_STEP_PERCENT * maximum() * (amount >= 0 ? 1 : -1)
      : HILL_CLIMBER_STEP_DECAY_RATE * amount;
  setPreviousSampleHitRate(hitRate);
  setAdjustment((long) amount);
  setStepSize(nextStepSize);
  setMissesInSample(0);
  setHitsInSample(0);
}
 
//减少protected区溢出的部分
@GuardedBy("evictionLock")
void demoteFromMainProtected() {
  long mainProtectedMaximum = mainProtectedMaximum();
  long mainProtectedWeightedSize = mainProtectedWeightedSize();
  if (mainProtectedWeightedSize <= mainProtectedMaximum) {
    return;
  }
  for (int i = 0; i < QUEUE_TRANSFER_THRESHOLD; i++) {
    if (mainProtectedWeightedSize <= mainProtectedMaximum) {
      break;
    }
    Node<K, V> demoted = accessOrderProtectedDeque().poll();
    if (demoted == null) {
      break;
    }
    demoted.makeMainProbation();
    accessOrderProbationDeque().add(demoted);
    mainProtectedWeightedSize -= demoted.getPolicyWeight();
  }
  setMainProtectedWeightedSize(mainProtectedWeightedSize);
}
 
//增加window区的大小
@GuardedBy("evictionLock")
void increaseWindow() {
  if (mainProtectedMaximum() == 0) {
    return;
  }
  long quota = Math.min(adjustment(), mainProtectedMaximum());
  setMainProtectedMaximum(mainProtectedMaximum() - quota);
  setWindowMaximum(windowMaximum() + quota);
  demoteFromMainProtected();
  for (int i = 0; i < QUEUE_TRANSFER_THRESHOLD; i++) {
    Node<K, V> candidate = accessOrderProbationDeque().peek();
    boolean probation = true;
    if ((candidate == null) || (quota < candidate.getPolicyWeight())) {
      candidate = accessOrderProtectedDeque().peek();
      probation = false;
    }
    if (candidate == null) {
      break;
    }
    int weight = candidate.getPolicyWeight();
    if (quota < weight) {
      break;
    }
    quota -= weight;
    if (probation) {
      accessOrderProbationDeque().remove(candidate);
    } else {
      setMainProtectedWeightedSize(mainProtectedWeightedSize() - weight);
      accessOrderProtectedDeque().remove(candidate);
    }
    setWindowWeightedSize(windowWeightedSize() + weight);
    accessOrderWindowDeque().add(candidate);
    candidate.makeWindow();
  }
  setMainProtectedMaximum(mainProtectedMaximum() + quota);
  setWindowMaximum(windowMaximum() - quota);
  setAdjustment(quota);
}
 
//和increaseWindow方法差不多
@GuardedBy("evictionLock")
void decreaseWindow() {
  if (windowMaximum() <= 1) {
    return;
  }
  long quota = Math.min(-adjustment(), Math.max(0, windowMaximum() - 1));
  setMainProtectedMaximum(mainProtectedMaximum() + quota);
  setWindowMaximum(windowMaximum() - quota);
  for (int i = 0; i < QUEUE_TRANSFER_THRESHOLD; i++) {
    Node<K, V> candidate = accessOrderWindowDeque().peek();
    if (candidate == null) {
      break;
    }
    int weight = candidate.getPolicyWeight();
    if (quota < weight) {
      break;
    }
    quota -= weight;
    setMainProtectedWeightedSize(mainProtectedWeightedSize() + weight);
    setWindowWeightedSize(windowWeightedSize() - weight);
    accessOrderWindowDeque().remove(candidate);
    accessOrderProbationDeque().add(candidate);
    candidate.makeMainProbation();
  }
  setMainProtectedMaximum(mainProtectedMaximum() - quota);
  setWindowMaximum(windowMaximum() + quota);
  setAdjustment(-quota);
}

算法

引言

缓存可以工作的最直观原因是在计算机科学的很多领域数据访问普遍存在着一定程度的局部性（locality）。

通过概率分布来捕获数据的局部性是一种常见方式，然而在很多领域概率分布是相当倾斜的，也就是说被高频访问的只是其中少部分对象。

而且，在不少场景中，访问模式及其对应的概率分布是随着时间的变化而变化的，即具有时间局部性（time locality）。

如果数据访问模式对应的概率分布不随时间变化，那使用LFU就可以获得最高的缓存命中率。但是LFU存在两个局限性：第一需要维护大量复杂的元数据（用于维护哪些元素应该写入缓存哪些应该被淘汰的空间叫做缓存的元数据）；第二在实际场景中访问频率随时间的推移发生根本变化，如热播剧在火了一段时间之后可能就无人问津了。针对上诉问题，出现了多种LFU的变种，主要采用老化机制或有限大小的采样窗口，目的是为了限制元数据的尺寸并将缓存和淘汰决策聚焦于最近流行的元素，Window LFU（WLFU）就是其中之一。

在绝大多数情况下，新访问的数据总是被直接插入到缓存中，缓存设计者仅关注于驱逐策略，这是因为维护当前不在缓存中的对象的元数据被认为是不切实际的。在LFU的已有实现中，都只维护了缓存中元素的频率直方图，这种LFU叫做In-Memory LFU。与之对应的是Perfect LFU（PLFU），维护所有访问过的对象的频率直方图，效果最佳但维护成本也高到令人望而却步。

LRU是一个很常见的用来替代LFU的算法，LRU的淘汰最近最少使用的元素，相较于LFU会有更加高效的实现，并自动适应突发的访问请求；然而基于LRU的缓存，要获得和LFU一样的缓存命中率通常需要更多的空间开销。

针对上述背景和问题，Ben Manes等人在论文 TinyLFU: A Highly Efficient Cache Admission Policy 中阐明了一种近似LFU准入策略的缓存结构/算法的有效性，为Caffeine缓存组件的合理性做了理论和实验论证。

其具体贡献如下：

提出了一种缓存结构，只有在准入策略认为将其替换进入缓存会提高缓存命中率的情况下才会被插入；
提出了一种空间利用率很高的新的数据结构——TinyLFU，可以在较大访问量的场景下近似的替代LFU的数据统计部分；
通过形式化的证明和模拟，证明了TinyLFU获得的Freq排序与真实的访问频率排序是几乎近似的；
以优化的形式将TinyLFU实现在了Caffeine项目中：W-TinyLFU；
与其他几种缓存管理策略进行了实验比较，包括ARC、LIRC等。

TinyLFU 结构

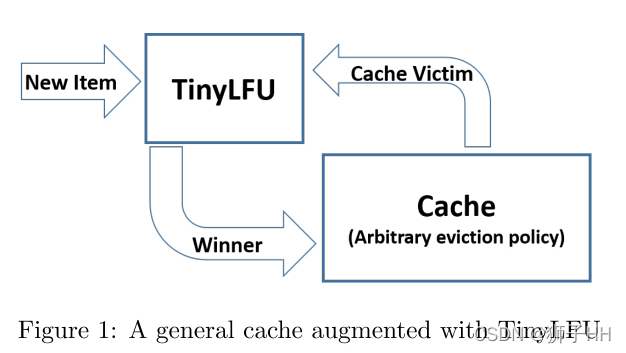
TinyLFU

TinyLFU的结构如图所示，对于被缓存驱逐策略判定为淘汰的元素，TinyLFU根据用新元素取代旧元素进入缓存是否有助于提高缓存命中率的原则来判断是否要进行替换。

为此，TinyLFU需要维护一份相当大的历史访问频率统计数据，这份开销是非常大的，因此TinyLFU使用了一些高效的近似计算技术来逼近这些统计数据.

近似计算

布隆过滤器（Bloom Filter）是由Howard Bloom在1970年提出的二进制向量数据结构，它具有很好的空间和时间效率（插入/查询时间都是常数），被用来检测一个元素是不是集合中的一个成员。

如果检测结果为是，该元素不一定在集合中；但如果检测结果为否，该元素一定不在集合中。由于布隆过滤器不需要存储元素本身，因此也适用于对保密要求严格的场景。

其缺点是随元素数量的增加，误算率随之增加，另外一点是不能删除元素，因为多个元素哈希的结果可能是同一位，删除一个比特位可能影响多个元素的检测。

计数式布隆过滤器Counting Bloom Filter（CBF）是在标准布隆过滤器的每一位上都额外增加了一个计数器，插入元素时给对应的k（哈希函数个数）个计数器分别加1，删除元素时分别减1.

最小增量(Minimal Increment) CBF是一种增强的计数式布隆过滤器，支持添加和评估（Estimate）两种方法。

评估方法先对key计算k个不同的hash值，以hash值作为索引读取对应的计数器，将这些计数器的最小值作为返回值。

添加方法与此类似，读到k个计数器后只增加最小的计数器。如下图所示，3个hash函数对应到3个计数器，读取到{2,2,5}，添加操作只会将2增加为3，5保持不变，以此对高频元素进行一个较好的估计，因为高频元素的计数器不太可能被很多低频元素增长。最小增量CBF不支持衰减，但经验表明这种方式可以减少高频计数的误差。

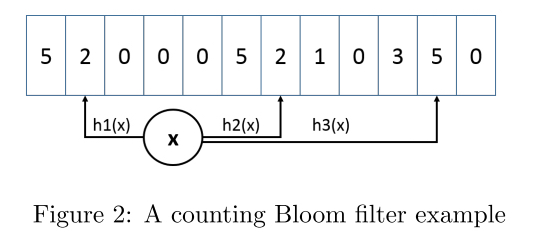
bloom-filter

CM-Sketch是另一种流行的近似计数方案，它在精度和空间之间做了权衡，以较小的精度损失换来了更小的空间占用和更快的速度。

而且，后文介绍的空间优化和老化机制可以直接适用于CM-Sketch.

新鲜度机制

目前已知的维护近似sketch（A sketch of a large amount of data is a small data structure that lets you calculate or approximate certain characteristics of the original data）的新鲜度的方式是使用一个包含m个不同的sketch的有序列表来进行滑动采样，新元素被插到第一个sketch，在一定数量的插入后最后一个sketch被清空并移到列表头，以此来将老的元素丢弃掉。

这种方式有两个缺点：

a) 为了评估一个元素的频率需要读取m个不同的近似sketch，导致许多内存访问和hash计算；

b) 因为要在m个不同的sketch中存储相同的元素并为每个元素分配更多计数器，所以空间开销增大了。

这对这两个问题，提出Reset方法来维护sketch的新鲜度。

Reset方法在每次将元素加到近似sketch时增加一个计数器，一旦计数器达到采样大小W，就将近似sketch中的所有计数器都除以2。这种直接除的方式有两个优点：首先不需要额外的空间开销，因为它的内存开销是一个占据Log(W)位的单个计数器；其次增加了高频元素的精确度。

这种方案的缺点是需要遍历所有计数器将其除以2，然而除2操作可以用移位寄存器在硬件上高效的实现，而且在软件实现时可以用移位和掩码来同时对多个小计数器执行此操作。

因此，除2操作的均摊复杂度是常数级别的，可适用于多种应用场景。

空间优化

空间优化有两种方式，一是降低sketch中每个计数器的大小，二是减少sketch内分配的计数器总数。

小计数器

近似sketch的实现一般用Long计数器，如果一个sketch要容纳W个请求，它要求计数器的最大值要达到W，每个计数器要占用Log(W)位，这种开销是很大的。考虑到频率直方图只需要知道待淘汰元素是否比当前被访问元素更受欢迎，而不必知道缓存中所有项之间的确切顺序，而且对于大小为C的缓存，所有访问频率在1/C以上的元素都应该属于缓存（合理假设被访问的元素总数大于C），因此对于给定的采样大小W，可将计数器的上限设置为W/C.

看门人机制

在很多场景尤其是长尾场景中，不活跃元素占据了相当大的比例，如果对每个元素统计访问次数就会出现大多数计数器被分配给了不太可能出现多次的元素，为了进一步缩减计数器的数量，使用看门人（Doorkeeper）机制来避免为尾部对象分配计数器。

Doorkeeper是一个放置于近似计数策略之前的常规布隆过滤器。当访问元素时，首先判断该元素是否在Doorkeeper中，如果不在则将该元素写入Doorkeeper，否则写入主结构。当查询元素时综合Doorkeeper和主结构一起计算，如果在Doorkeeper中，则将主结构中元素的次数加1，不在则直接返回主结构中次数。当进行Reset操作时，会将主结构中所有计数器减半并同时清空Doorkeeper。通过这种方式可以清除所有第一次计数器的信息（也会使截断错误加1）。

在内存方面，尽管Doorkeeper需求额外的空间，但它通过限制写入主结构中的元素数量使得主结构更小，尤其是在长尾场景中，大部分长尾元素只占用了Doorkeeper中的1bit计数器，因此该优化会极大的降低TinyLFU的内存开销。

Doorkeeper 在TinyLFU中的结构如图所示。

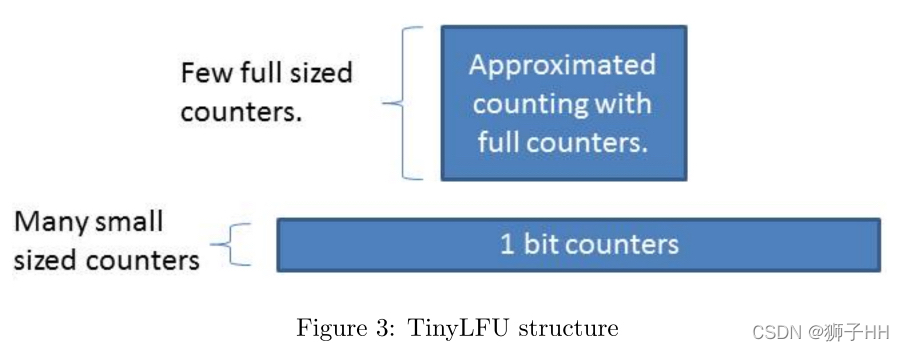
Doorkeeper

W-TinyLFU 优化

TinyLFU在大多数场景下表象良好，但对于有稀疏爆发流量的场景，当新爆发的流量不能累积足够的次数以使得它留在缓存中时，就会导致这些元素被淘汰，会出现反复miss的情况。

该问题在将TinyLFU集成到Caffeine中时通过引入W-TinyLFU结构予以补救。

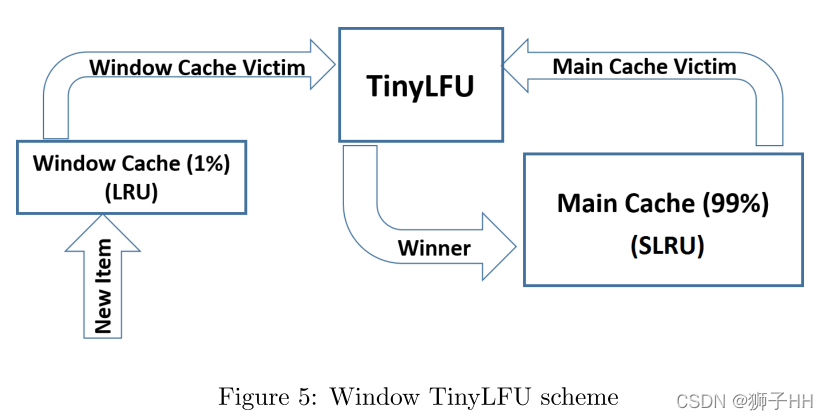
W-TinyLFU

W-TinyLFU的结构如图所示，它由两个缓存单元组成，主缓存使用SLRU驱逐策略和TinyLFU准入策略，window cache仅使用LRU驱逐策略无准入策略。

主缓存中的SLRU策略的A1和A2区域被静态划分开来，80%空间被分配给热点元素（A2），被驱逐者则从20%的非热项(A1)中选取。

任何到来的元素总是允许进入window cache，window cache的淘汰元素有机会进入主缓存，如果被主缓存接受，那么W-TinyLFU的淘汰者就是主缓存的淘汰者，否则则是window cache的淘汰者。

在Caffeine中，window cache占总缓存的1%，主缓存占99%。W-TinyLFU背后的动机是以TinyLFU的方式处理LFU的工作，同时仍然能够利用LRU应对突发流量的优势。

因为99%的缓存分配给主缓存，所以对LFU工作的性能影响是微不足道的。另

一方面，在适用于LRU的场景中，W-TinyLFU比TinyLFU更好。

总的来说，W-TinyLFU在各种业务场景都是首要选择，因此将其引入Caffeine所带来的复杂度是可以接受的。

优雅的实现

Caffeine 的主要功能如图所示。

支持手动/自动、同步/异步多种缓存加载方式，支持基于容量、时间及引用的驱逐策略，支持移除监听器，支持缓存命中率、加载平均耗时等统计指标。

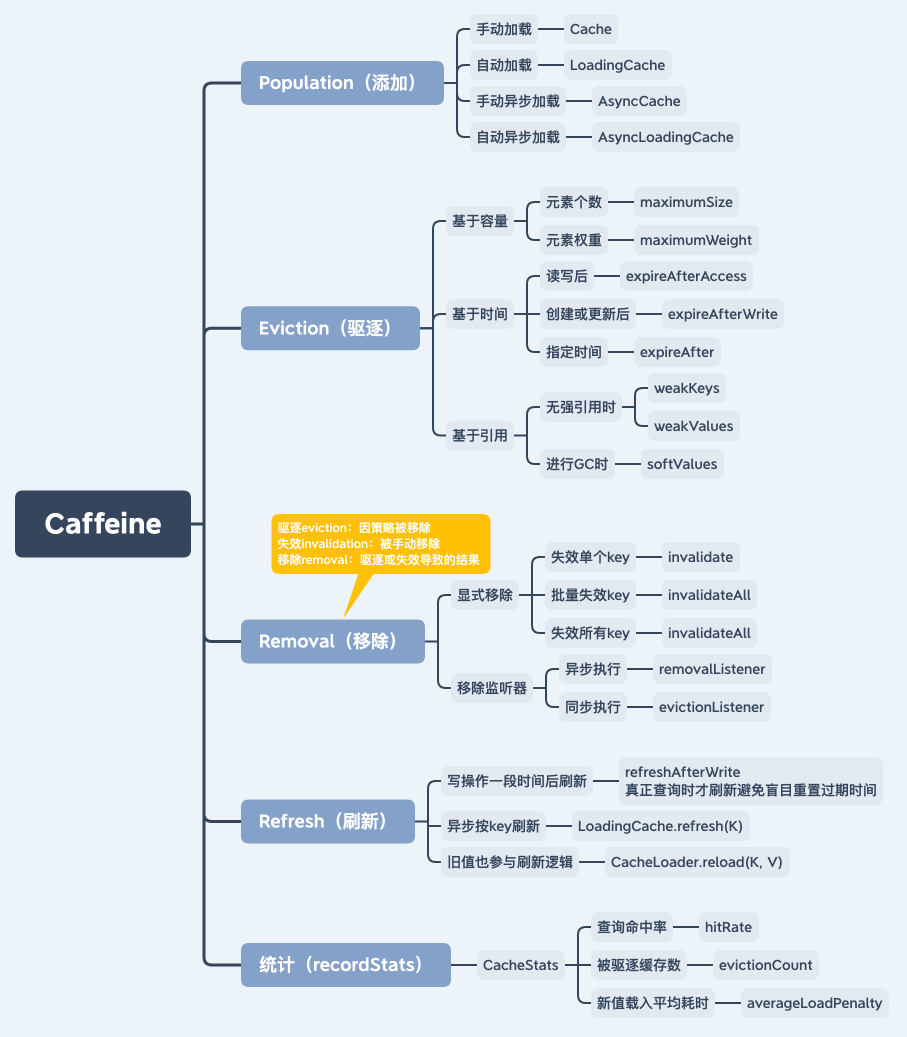
Caffeine

整体设计

一些能力

顺序访问队列

访问队列（Access order queue）是一个双向链表，其将所有HashTable中的元素有序排列在其中。

一个元素可以在O(1)的时间复杂度内从HashMap中找到并操作队列中与其相邻的元素。访问顺序被定义为缓存中的元素被创建、更新或访问的顺序。最近最少被使用的元素将会在队首，而最近被使用的元素将会在队列末尾。这为基于容量的驱逐策略(maximumSize)和基于空闲时间的过期策略(expireAfterAccess)的实现提供了帮助。这里的问题在于，每次访问都会对队列进行更改，因此无法通过高效的并发操作来实现。

顺序写队列

写顺序被定义为缓存中的元素被创建和更新的顺序。和访问队列类似，写队列的操作也都是基于O(1)的时间复杂度。这个队列为基于存活时间的驱逐策略(expireAfterWrite)的实现提供帮助。

分层时间轮

分层时间轮是一个用hash和双向链表实现的以时间作为优先级的优先队列，其操作也是O(1)的时间复杂度。这个队列为基于指定时间的驱逐策略(expireAfter(Expiry))的实现提供帮助。

读缓冲

典型的缓存实现会为每个操作加锁，以便能够安全的对每个访问队列的元素进行排序。一种替代方案是将每个重新排序的操作加入到缓冲区中进行批处理操作。这可以当作页面置换（page replacement）策略的预写日志。当缓冲区满的时候，将会尝试获取锁并挂起，如果持有了锁则线程会立即返回。

读缓冲是一个带状环形缓冲区（striped ring buffer）。带状的设计是为了减少线程之间的资源竞争，一个线程通过hash对应到一个带上。环形缓冲是一个定长数组，提供高效的性能并最大程度上减少GC开销。而环形队列的具体数量可以根据竞争预测算法进行动态调整。

写缓冲

与读缓冲类似，写缓冲是为了重放写事件。读缓冲中的事件主要是为了优化驱逐策略的命中率，因此允许一定程度的有损。但是写缓冲并不允许数据的丢失，因此其必须实现为一个高效的有界队列。由于每次向写缓冲填充的时候都要清空写缓冲中的内容，因此通常情况下写缓冲的容量都为空或者很小。

写缓冲区由一个可扩展至最大大小的环形数组所实现。当调整数组大小的时候将会直接分配内存生成一个新的数组。而前置数组将会指向新的数组以便消费者可以访问，这允许旧的数组访问后可以直接释放。这种分块机制允许缓冲区可以拥有一个较小的初始大小，较低的读写成本并且产生较小的垃圾。当缓冲区被写满并无法扩容的时候，缓冲区的生产者将会尝试自旋并触发维护操作，并在短暂的时间后返回可执行状态。这样可以使消费者线程通过重放驱逐策略上的写入来确定优先级并清空缓存区。

锁均摊

传统缓存会给每个操作加锁，而Caffeine则通过批处理将加锁开销分摊到各个线程中。这样，锁带来的副作用将由各线程均摊而避免加锁竞争带来的性能开销。维护操作将会分发给所配置的线程池进行执行，在任务被拒绝或者指定调用线程执行策略下，也可以由使用者线程进行维护操作。

批处理的一个优势在于，由于锁的排他性，同一时间将只会有一个线程处理缓冲区内的数据。这将使得基于多生产者/单消费者的消费模型缓冲区实现更加高效。这也将更好地利用CPU缓存优势来更适应硬件特性。

元素状态转换

当缓存不被一个排他锁保护的时候，针对缓存的操作可能以错误的顺序进行重放。在并发竞争条件下，一个创建-读取-更新-删除的顺序操作可能无法以正确顺序写入缓存。如果要保证顺序正确，可能需要更粗粒度的锁从而导致性能下降。

与典型的并发数据结构一样，Caffeine使用原子状态转变来解决这一难题。一个缓存元素具有存活，退休，死亡三种状态。存活状态是指某一元素同时存在与Hash表和访问/写队列中。而一个元素从Hash表中被移除的时候，其状态也将变为退休并需要从队列中移除。当从队列中也被移除后，一个元素的状态将会被视为死亡并在GC中被回收。

Relaxed reads and writes

Caffeine 对充分利用volatile操作花费了很多精力。

内存屏障提供了一种从硬件角度出发的视角来代替从语言层面思考volatile的读写。通过了解哪些屏障被建立以及它们对硬件和数据可见性的影响，将具有实现更好性能的潜力。

当在锁下进行独占访问的时候，Caffeine使用relaxed reads, 因为数据的可见性可以通过锁的内存屏障获取。这在数据竞争无法避免的情况下（比如在读取元素时校验是否过期来模拟缓存丢失）是可以接受的。

Caffeine 以相似的方式使用relaxed writes。当一个元素在锁定状态进行排他写，那么这次写入可以搭载在解锁时释放的内存屏障上返回。这也可以用来支持解决写偏序问题，比如在读取一个数据的时候更新其时间戳。

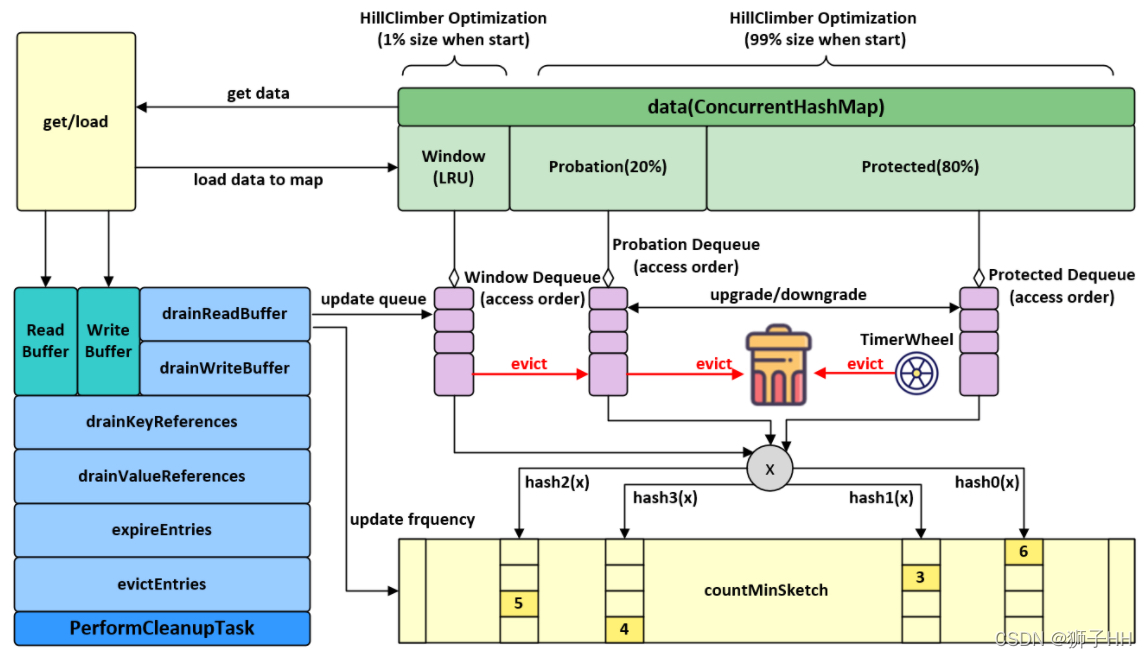
驱逐策略

Caffeine 使用 Window TinyLfu策略提供了几乎最优的命中率。访问队列被分为两个部分：TinyLfu策略将会从缓存的准入窗口中选择元素驱逐到缓存的主空间当中。TinyLfu会比较窗口中的受害者和主空间的受害者之间的访问频率，选择保留两者之间之前被访问频率更高的元素。频率将在CountMinSketch中通过4位存储，这将为每个元素占用8个字节去计算频率。这些设计允许缓存能够以极小的代价基于访问频率和就近程度去对缓存中的元素进行O(1)时间复杂度的驱逐操作。

自适应性

准入窗口的大小和主空间的大小将会基于缓存的工作负载特征动态调节。当更加偏向就近度的时候，窗口将会更大，而偏向频率的时候窗口则将更小。Caffeine使用了hill climbing算法去采样命中率来调整，并将其配置为最佳的平衡状态。

快速处理模式

当缓存的大小还未超过总容量的 50%，驱逐策略也未用的时候，用来记录频率的sketch将不会初始化以减小内存开销，因为缓存可能人为地给了一个较高的阈值进行加载。当没有其他特性要求的时候，访问将不会被记录，以避免读缓冲上的竞争和重放读缓冲上的访问事件。

HashDoS 保护

当key之间的hash值相同，或者hash到了同一个位置，这类的hash冲突可能会导致性能降低。hash表采用将链表降级为红黑树的方法来解决该问题。

一种针对TinyLFU的攻击是利用hash冲突来人为地提高驱逐策略下的元素的预估频率。这将导致所有后续进入的元素被频率过滤器所拒绝，导致缓存失效。一种解决方案是加入少量抖动使得最后的结果具有一定的不确定性。这可通过随机录取约1%的被拒绝的候选人来实现。

代码生成

Cache 有许多不同的配置，只有使用特定功能的子集的时候，相关字段才有意义。如果默认情况下所有字段都存在，将会导致缓存和每个缓存中的元素的内存开销的浪费。使用代码生成将会减少运行时的内存开销，其代价是需要在磁盘上存储更大的二进制文件。

这项技术有通过算法优化的潜力。也许在构造的时候用户可以根据用法指定最适合的特性。一个移动应用可能更需要更高的并发率，而服务器可能需要在一定内存开销下更高的命中率。也许不需要通过不断尝试在所有用法中选择最佳的平衡，而可以通过驱动算法进行选择。

被封装的hash map

缓存通过在ConcurrentHashMap之上进行封装来添加所需要的特性。缓存和hash表的并发算法非常复杂。通过将两者分开，可以更便利地应用hash表的设计的优秀之处，也可以避免更粗粒度的锁覆盖全表和驱逐所引发的问题。

这种方式的成本是额外的运行时开销。这些字段可以直接内联到表中的元素上，而不是通过包装容纳额外的元数据。

缺少包装可以提供单次表操作的快速路径（比如lambdas）而不是多次map调用和短暂存活的对象实例。

参考资料

https://blog.csdn.net/xiaodigua1024/article/details/129311453

本地缓存之王-Caffeine

https://blog.csdn.net/A_art_xiang/article/details/134573115

https://blog.51cto.com/u_14251143/5339023

https://blog.csdn.net/chuige2013/article/details/130940330

1、FIFO(先进先出)算法
2、LRU(最近最久未使用)算法
3、LFU(最近最少使用)算法
4、TinyLFU 算法
5、W-TinyLFU 算法
四、Caffeine 代码实现
- 相关代码：
算法
- 引言
TinyLFU 结构
W-TinyLFU 优化
优雅的实现
- 整体设计
- 一些能力
参考资料

Caffeine-03-过期策略淘汰算法 FIFO/LRU/LFU/TinyLFU 算法

1、FIFO(先进先出)算法

2、LRU(最近最久未使用)算法

3、LFU(最近最少使用)算法

4、TinyLFU 算法

5、W-TinyLFU 算法

四、Caffeine 代码实现

相关代码：

1.Count–Min Sketch算法写入频率和查询频率和保新机制代码实现：

2.evictEntries()淘汰方法入口：

3.动态调整window区和protected区的大小 climb()方法：

算法

引言

TinyLFU 结构

近似计算

新鲜度机制

空间优化

小计数器

看门人机制

W-TinyLFU 优化

优雅的实现

整体设计

一些能力

顺序访问队列

顺序写队列

分层时间轮

读缓冲

写缓冲

锁均摊

元素状态转换

Relaxed reads and writes

驱逐策略

自适应性

快速处理模式

HashDoS 保护

代码生成

被封装的hash map

参考资料

更多学习

1、FIFO(先进先出)算法

2、LRU(最近最久未使用)算法

3、LFU(最近最少使用)算法

4、TinyLFU 算法

5、W-TinyLFU 算法

四、Caffeine 代码实现

相关代码：

1.Count–Min Sketch算法写入频率 和 查询频率 和 保新机制 代码实现：

2.evictEntries()淘汰方法入口：

3.动态调整window区和protected区的大小 climb()方法：

算法

引言

TinyLFU 结构

近似计算

新鲜度机制

空间优化

小计数器

看门人机制

W-TinyLFU 优化

优雅的实现

整体设计

一些能力

顺序访问队列

顺序写队列

分层时间轮

读缓冲

写缓冲

锁均摊

元素状态转换

Relaxed reads and writes

驱逐策略

自适应性

快速处理模式

HashDoS 保护

代码生成

被封装的hash map

参考资料

更多学习

1.Count–Min Sketch算法写入频率和查询频率和保新机制代码实现：