Red Black Tree
红黑树(英语:Red–black tree)是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。
它是在1972年由鲁道夫·贝尔发明的,他称之为”对称二叉B树”,它现代的名字是在Leo J. Guibas和Robert Sedgewick于1978年写的一篇论文中获得的。
它是复杂的,但它的操作有着良好的最坏情况运行时间,并且在实践中是高效的:它可以在 O(lg(n)) 时间内做查找,插入和删除,这里的 n 是树中元素的数目。
用途和好处
红黑树和AVL树一样都对插入时间、删除时间和查找时间提供了最好可能的最坏情况担保。
这不只是使它们在时间敏感的应用如实时应用(real time application)中有价值,而且使它们有在提供最坏情况担保的其他数据结构中作为建造板块的价值;
例如,在计算几何中使用的很多数据结构都可以基于红黑树。
红黑树在函数式编程中也特别有用,在这里它们是最常用的持久数据结构(persistent data structure)之一,它们用来构造关联数组和集合,每次插入、删除之后它们能保持为以前的版本。
除了 O(lg(n)) 的时间之外,红黑树的持久版本对每次插入或删除需要 O(lg(n)) 的空间。
红黑树是2-3-4树的一种等同。
换句话说,对于每个2-3-4树,都存在至少一个数据元素是同样次序的红黑树。
在2-3-4树上的插入和删除操作也等同于在红黑树中颜色翻转和旋转。
这使得2-3-4树成为理解红黑树背后的逻辑的重要工具,这也是很多介绍算法的教科书在红黑树之前介绍2-3-4树的原因,尽管2-3-4树在实践中不经常使用。
红黑树相对于AVL树来说,牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作,整体来说性能要优于AVL树。
性质
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
-
节点是红色或黑色。
-
根是黑色。
-
所有叶子都是黑色(叶子是NIL节点)。
-
每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
-
从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

- 约束的作用
这些约束确保了红黑树的关键特性:从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。
因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
要知道为什么这些性质确保了这个结果,注意到性质4导致了路径不能有两个毗连的红色节点就足够了。
最短的可能路径都是黑色节点,最长的可能路径有交替的红色和黑色节点。
因为根据性质5所有最长的路径都有相同数目的黑色节点,这就表明了没有路径能多于任何其他路径的两倍长。
在很多树数据结构的表示中,一个节点有可能只有一个子节点,而叶子节点包含数据。用这种范例表示红黑树是可能的,但是这会改变一些性质并使算法复杂。
为此,本文中我们使用”nil叶子”或”空(null)叶子”,如上图所示,它不包含数据而只充当树在此结束的指示。
这些节点在绘图中经常被省略,导致了这些树好像同上述原则相矛盾,而实际上不是这样。
与此有关的结论是所有节点都有两个子节点,尽管其中的一个或两个可能是空叶子。
自平衡策略
对于一棵红黑树的操作最基本的无外乎增删改查,其中查和改都不会改变树的结构,所以与普通平衡二叉树操作无异。
剩下的就是增删操作,插入和删除都会破坏树的结构,不过借助一定的平衡策略能够让树重新满足定义。
平衡策略可以简单概括为三种:左旋转、右旋转,以及变色。
在插入或删除结点之后,只要我们沿着结点到根的路径上执行这三种操作,就可以最终让树重新满足定义。
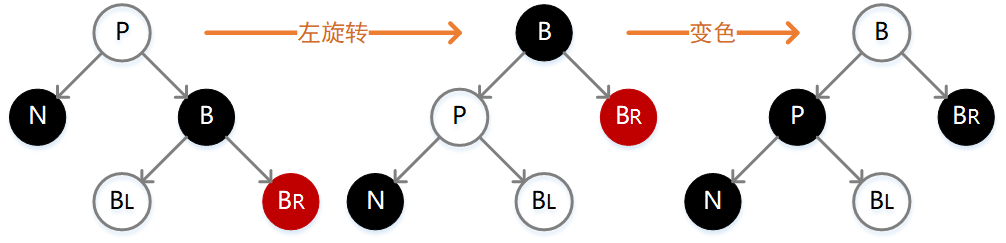
左旋转
对于当前结点而言,如果右子结点为红色,左子结点为黑色,则执行左旋转,如下图:
右旋转
对于当前结点而言,如果左子、左孙子结点均为红色,则执行右旋转,如下图:

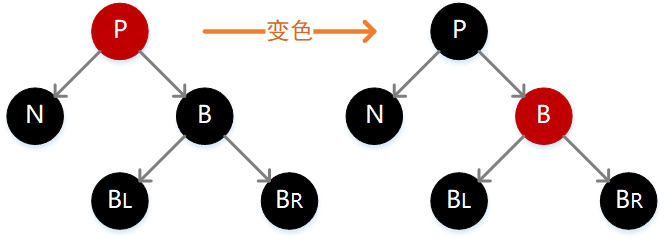
变色
对于当前结点而言,如果左、右子结点均为红色,则执行变色,如下图:

区分左旋和右旋
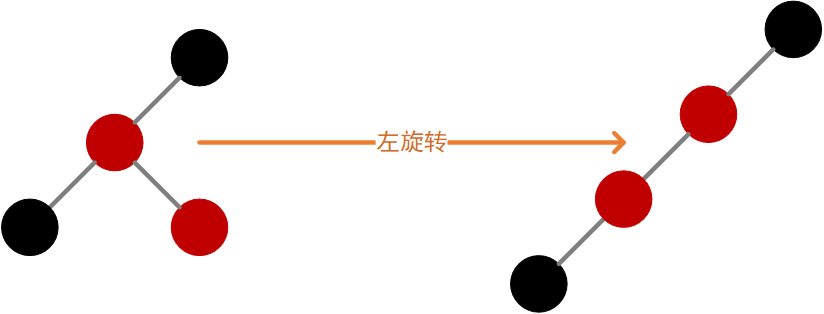
仔细观察上面”左旋”和”右旋”的示意图。
我们能清晰的发现,它们是对称的。无论是左旋还是右旋,被旋转的树,在旋转前是二叉查找树,并且旋转之后仍然是一颗二叉查找树。

左旋示例图
(以x为节点进行左旋)
z
x /
/ \ --(左旋)--> x
y z /
y
对x进行左旋,意味着,将“x的右孩子”设为“x的父亲节点”;即将 x 变成了一个左节点(x成了为z的左孩子)。
因此,左旋中的“左”,意味着“被旋转的节点将变成一个左节点”。
右旋示例图(以x为节点进行右旋):
y
x \
/ \ --(右旋)--> x
y z \
z
对x进行右旋,意味着,将“x的左孩子”设为“x的父亲节点”;即将 x 变成了一个右节点(x成了为y的右孩子)。
因此,右旋中的“右”,意味着“被旋转的节点将变成一个右节点”。
插入操作
红黑树作为平衡二叉树的一种,同样需要借助于查找操作定位插入点,不过红黑树约定: 新插入的结点一律为红色,这主要也是为了简化树的自平衡过程。
对于一棵空树而言,插入结点为红色会增加一次变色操作,但是对于其余的情况,如果插入的结点是一个黑色结点,那么必然会破坏性质 5,而插入一个红色结点有可能会破坏性质 4,但是此时我们可以通过简单的策略对树进行调整以重新满足定义。
我们约定 X 为插入的结点,P 为 X 的父结点,G 为 X 的祖父结点,U 为 X 的叔叔结点。
下面遵从上述策略分场景对插入过程进行探讨:
1. 新插入结点 X 是根结点
此时新插入结点为红色,违背性质 2,只需将其变为黑色即可。
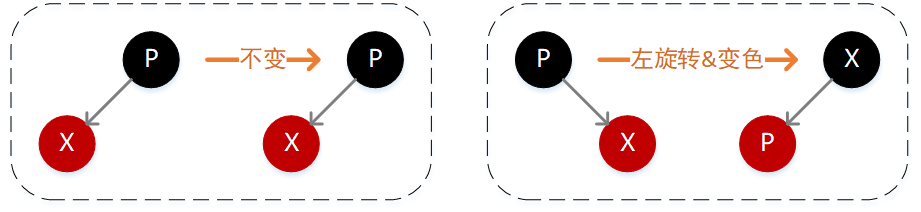
2. 新插入结点 X 的父结点 P 是黑色
此时需要依据新插入结点 X 值相对于父结点 P 的大小分为两种情况。
如果小于则将 X 简单插入到 P 的左子位置即可(下图左),如果 X 的值大于 P,则需要将 X 插入到 P 的右子结点位置,然后执行一次左旋转即可(下图右)。
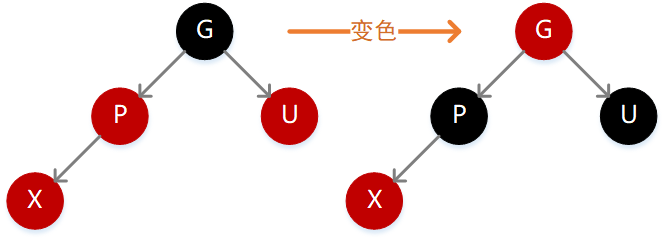
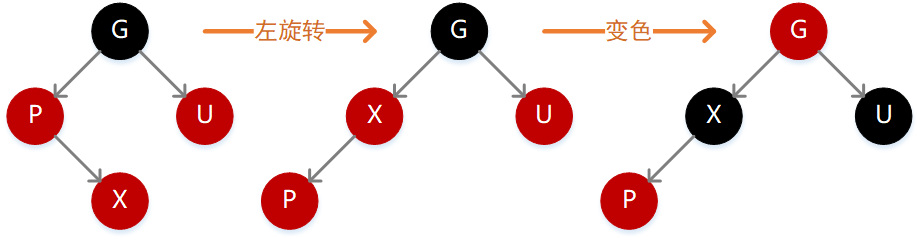
3. 父结点 P 为红色,同时存在叔叔结点 U 也为红色
因为 P 为红色,按照性质 4 则 G 必定为黑色,如果 X 的值小于 P,则需要在 P 的左子位置插入(如下图),
插入后不满足性质 4,此时只需要执行一次变色操作,将 P、G、U 的颜色反转一下即可,因为 G 变为红色,所以路径长度减 1,但是因为 P 和 U 都变为了黑色,所以路径长度又加 1,最终长度不变,但此时 G 变为了红色,所以需要继续向上递归。
如果 X 的值大于 P,则需要在 P 的右子位置插入(如下图),插入后不满足性质 4,此时需要先执行左旋转变为上面这种情况,继续变色即可。
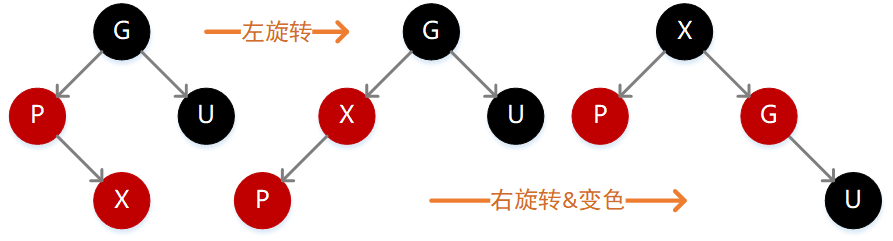
4. 父结点 P 为红色,同时叔叔结点 U 为黑色或不存在
因为 P 为红色,按照性质 4 则 G 必定为黑色,如果 X 的值小于 P,则需要在 P 的左子位置插入(如下图),
插入后不满足性质 4,此时需要先执行一次右旋转,旋转之后仍然违背性质 4,同时左子树的高度减 1,这个时候需要再执行一次变色操作即可满足定义。

如果 X 的值大于 P,则需要在 P 的右子位置插入(如下图),插入后不满足性质 4,此时我们需要执行一次左旋转,然后就转换成了上面这种情况,继续右旋转、变色即可。
删除操作
红黑树作为平衡二叉树的一种,同样需要借助于查找操作定位删除点,在执行删除之前我们需要判断待删除结点有几个孩子结点,如果是 2 个的话我们需要从结点的左子树中寻找值最大的结点,或者从右子树中寻找值最小的结点,并用结点值替换掉待删除结点(只要目标结点值从树上消失即可,不要纠结具体删除的是哪个结点)。
这两个结点有一个共性,即最多只有一个孩子结点(因为已经是自己所处范围内的最大和最小了嘛,一山不容二虎(鼠)),此时就将需求转变成删除只有一个孩子结点的结点,相对要简单了许多。
我们约定 X 为待删除的结点,P 为 X 的父结点,S 为 X 的孩子结点,B 为 X 的兄弟结点,BL 为 B 的左孩子结点,BR 为 B 的右孩子结点。
-
如果待删除结点 X 是一个红色结点,则直接删除即可,不会违反定义。
-
如果待删除结点 X 是一个黑色结点,且其孩子结点 S 是红色的,那么只需要将 X 替换成 S,同时将 S 由红变黑即可。
-
如果需要删除的结点 X 是黑色的,同时它的孩子结点 S 也是黑色的,这种情况需要进一步分场景讨论。
对于第三种情况我们首先将 X 替换成 S,并重命名其为 N,N 沿用 X 对于长辈和晚辈的称呼,需要清楚这里实际删除的是 X 结点,并且删除之后通过 N 的路径长度减 1。
1. N 是新的根
这种情况比较简单,不需要再做任何调整。
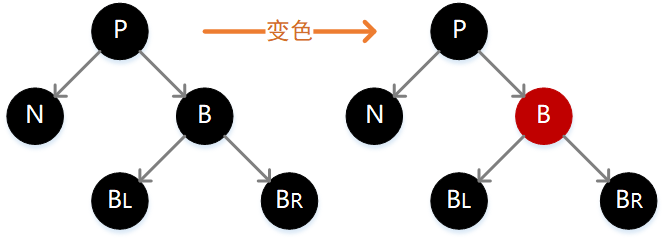
2. N 的父结点、兄弟结点 B,以及 B 的孩子结点均为黑色
如下图,此时只需要将 B 变为红色即可,这样所有通过 B 的路径减 1,与所有通过 N 的路径正好一致,但是此时通过 P 的路径都减少了 1 个长度,所以需要向上递归对结点 P 继续判定。
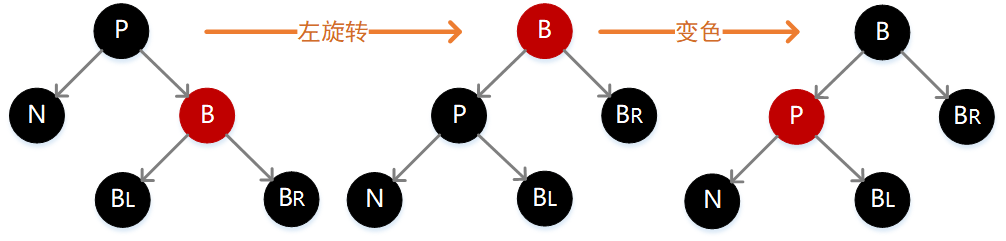
3. N 的兄弟结点 B 为红色,其余结点均为黑色
如下图,此时需要执行一次左旋转,然后将 P 和 B 的颜色互换。
调整前后各个结点的路径没有变化,但是因为之前经过 N 的路径长度少了一个单位,所以此时仍然不满足定义,需要按照后面的场景继续调整。
4. N 的父结点 P 为红色,兄弟结点 B,以及 B 的孩子结点均为黑色
如下图,此时我们只需要简单互换 P 和 B 的颜色,这种情况下对于不通过 N 的结点路径没有影响,但是却让通过 N 的结点路径加 1,正好弥补之前删除操作所带来的损失。
5. N 的兄弟结点 B 为黑色,B 的左孩子为红色,B 的右孩子为黑色
如下图,此时我们需要先执行一次右旋转操作,然后互换 B 与 BL 的颜色,操作之后通过所有结点的路径长度并没有发生变化,却让 N 有了一个新的黑色兄弟结点,并且该兄弟结点的右孩子为红色,从而可以按照接下去介绍的一种场景继续调整。

注:白色结点表示该结点既可以是黑色也可以是红色,后续图示亦是如此。
6. N 的兄弟结点 B 为黑色,B 的右孩子为红色
如下图,此时我们需要先执行一次左旋转,并互换 P 和 B 的颜色,同时将 B 的右孩子结点变为黑色。
变更之后,除 N 外其余结点的路径长度未发生变化,但是经过 N 的路径上却增加了一个黑色结点,这刚好弥补之前删除操作所带来的损失。