索引概述
定义:索引是存储引擎用于快速找到记录的一种数据结构。
举例说明:如果查找一本书中的某个特定主题,一般会先看书的目录(类似索引),找到对应页面。
在MySQL,存储引擎采用类似的方法使用索引,高效获取查找的数据。
索引的优缺点
优点
提高查询语句的执行效率,减少 IO 操作的次数
创建唯一性索引,可以保证数据库表中每一行数据的唯一性
加了索引的列会进行排序(一本书的章节顺序不就是按照目录来排嘛),在使用分组和排序子句进行查询时,可以显著减少查询中分组和排序的时间
缺点
索引需要占物理空间
创建索引和维护索引要耗费时间,这种时间随着数据量的增加而增加
当对表中的数据进行增删改查是,索引也要动态的维护,这样就降低了数据的更新效率
索引的分类
1)从存储结构上来划分
Btree 索引(B+tree,B-tree)
哈希索引
full-index 全文索引
2)从应用层次上来划分
普通索引:即一个索引只包含单个列,一个表可以有多个单列索引。
唯一索引:索引列的值必须唯一,但允许有空值。
复合索引:一个索引包含多个列。
3)从表记录的排列顺序和索引的排列顺序是否一致来划分
聚集索引:表记录的排列顺序和索引的排列顺序一致。
非聚集索引:表记录的排列顺序和索引的排列顺序不一致。
索引底层数据结构
磁盘IO与预读
数据库保存的数据是存储在磁盘上,查找数据时需要将磁盘中的数据加载到内存中,在介绍索引的实现之前,先了解下磁盘IO与预读。
磁盘读取数据靠的是机械运动,每次读取数据花费的时间可以分为寻道时间、旋转延迟、传输时间三个部分,寻道时间指的是磁臂移动到指定磁道所需要的时间,主流磁盘一般在5ms以下;
旋转延迟就是我们经常听说的磁盘转速,比如一个磁盘7200转,表示每分钟能转7200次,也就是说1秒钟能转120次,旋转延迟就是1/120/2 = 4. 17ms;
传输时间指的是从磁盘读出或将数据写入磁盘的时间,一般在零点几毫秒,相对于前两个时间可以忽略不计。
那么访问一次磁盘的时间,即一次磁盘IO的时间约等于5+4. 17 = 9ms左右,听起来还挺不错的,但要知道一台500 -MIPS的机器每秒可以执行5亿条指令,因为指令依靠的是电的性质,换句话说执行一次IO的时间可以执行40万条指令,数据库动辄十万百万乃至千万级数据,每次9毫秒的时间,显然是个灾难。
下图是计算机硬件延迟的对比图,供大家参考:
考虑到磁盘IO是非常高昂的操作,计算机操作系统做了一些优化,当一次IO时,不光把当前磁盘地址的数据,而是把相邻的数据也都读取到内存缓冲区内。
因为局部预读性原理告诉我们,当计算机访问一个地址的数据的时候,与其相邻的数据也会很快被访问到。
每一次IO读取的数据我们称之为一页(page)。
具体一页有多大数据跟操作系统有关,一般为4k或8k,也就是我们读取一页内的数据时候,实际上才发生了一次IO,这个理论对于索引的数据结构设计非常有帮助。
索引的内存模型
实现索引的方式有很多种,这里先介绍下最常见的三种:哈希表、有序数组、二叉树,其中二叉树又分为二叉查找树、平衡二叉树、B 树以及 B+ 树,从而说明为啥 InnDB 选择了 B+ 树?
哈希表
HashMap 相信大家都用过,哈希表就是一种以键值对存储数据的结构。
在 MySQL 中 key 用于存储索引列,value 就是某行的数据或者是它的磁盘地址。
用过 HashMap 的你可能知道了,当多个 key 经过哈希函数换算之后会出现同一个值,这种情况下就会 value 值的结构就是个链表。
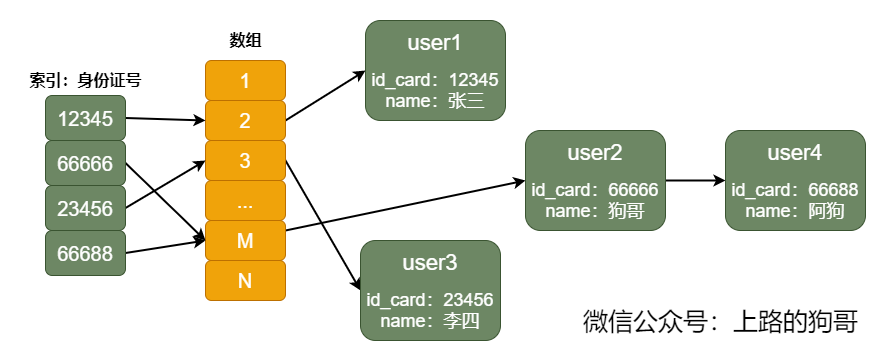
假设现在让你通过身份证号找名字,这时它的哈希表索引结构是这样的:
从上图可知,user2 和 user4 哈希出来的 key 值都是 M,这个时候 value 的值就是个链表。
如果你要查 id_card = 66688 的人,步骤是:先将 66688 通过哈希函数算出 M,然后按顺序遍历链表,找到 user2。
你可能注意到了上图中四个 id_card 的值并不是递增的,所以增加新 user 时速度会很快,往后追加就好。
但又因为不是有序的,做区间查询的速度就会很慢。
所以,哈希表结构适用于只有等值查询的场景,不适合范围查询。
有序数组
为了解决区间查询速度慢的问题,有序数组应运而生。
它的等值和范围查询都很快。
还是上面根据身份号找用户的例子,这时候的索引结构是这样的:
身份证号递增且不重复从而有以上有序数组,这是如果你要查 id_card = 66666 的用户,用二分法就可以啦,复杂度是 O(log(N))。
这数组还支持范围查询,还是用二分查找法,如果你要查区间 [12345,66666]的用户,只需要二分查找出 id_card 大于等于 12345 且小于 66666 的用户即可。
单看查询效率,有序数组简直完美,但是如果我们要新增数据就很很难受了。
假设你要新增 id_card = 12346 的用户,那就只能把后面的数据都往后挪一个位置,成本太高了。
所以有序数组只适用于存储一些不怎么变的数据,比如一些过去的年份数据。
二叉搜索树
二叉搜索树,也称二叉查找树,或二叉排序树。
其定义也比较简单,要么是一颗空树,要么就是具有如下性质的二叉树:每个节点只有两个分叉,左子树所有节点值比右子树小,每个节点的左、右子树也是一个小的二叉树,且没有健值相等的节点。
说概览有点懵,先上个图。
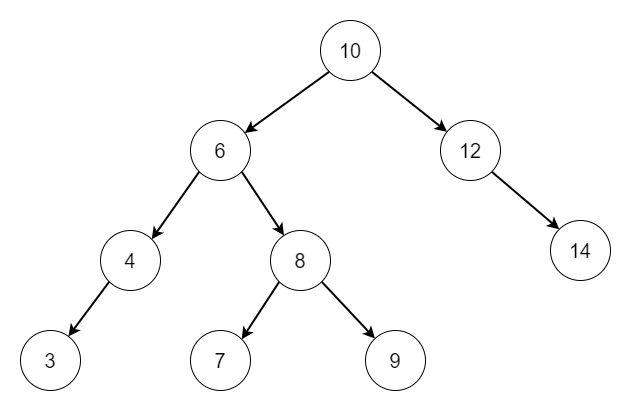
一般的二叉搜索树长这样:
之所以设计成二叉有序的结构是因为可以利用二分查找法,它的插入和查找的时间复杂度都是 O(log(N)),但是最坏情况下,它的时间复杂度是 O(n),原因是在插入和删除的时候树没有保持平衡。
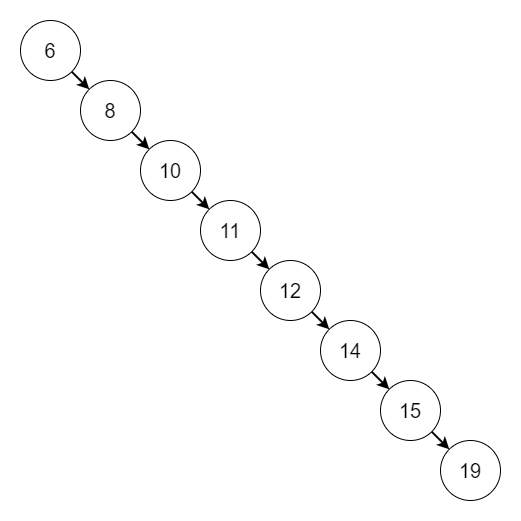
比如顺拐的二叉树:
所以这种情况下,树的查询时间复杂度都变高,而且也不稳定。
平衡二叉树
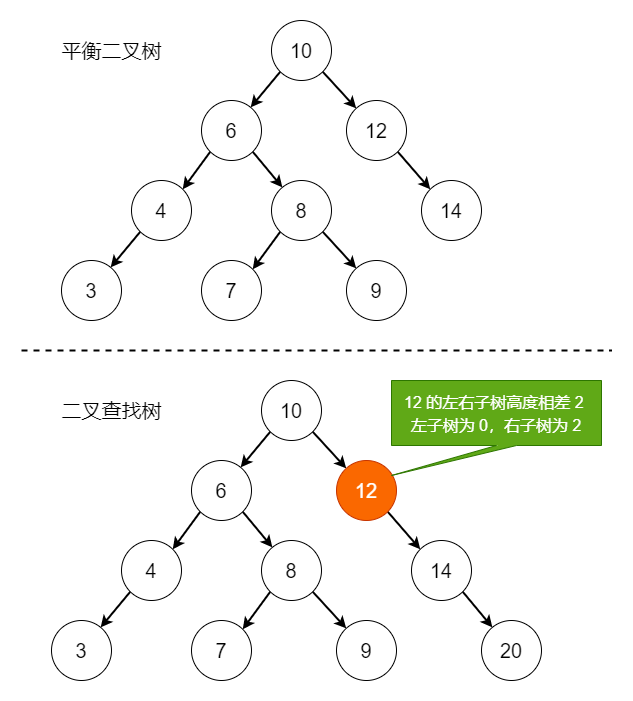
平衡二叉树也叫 AVL 树,它与二叉查找树的区别在于平衡,它任意的左右子树之间的高度差不大于 1。
我做了个对比,如下图:
这样就很开心了,根据平衡二叉树的特点。
它的查询时间复杂度是 O(log(N)),当然为了维护平衡它更新的时间复杂度也是 O(log(N))。
貌似完美?但是还有问题。
学过数据结构都知道,时间复杂度与树高相关。你想想假设现在有一颗 100 万节点的平衡二叉树,树高 20。一次查询需要访问 20 个数据块。
而根据计算机组成原理得知,从磁盘读一个数据快平均需要 10ms 的寻址时间。
PS:索引不止存在内存中,还会写到磁盘上,所以优化的核心在于减少磁盘的 IO 次数。
也就是说,对于一个 100 万行的表,如果使用平衡二叉树来存储,单独访问一行可能需要 20 个 10ms 的时间,也就是 0.2s,这很难受了。
此外,平衡二叉树不支持快速的范围查询,范围查询时需要从根节点多次遍历,查询效率真心不高。
所以,大多数的数据库存储也并不使用平衡二叉树。
B-tree
上面分析我们知道了,查询慢是因为树高,要多次访问磁盘。为了让一个查询尽量少触及磁盘。
我们可以降低树的高度,既然有二叉。
那我们多分几个叉,树的高度不就降低了?
所以,这时就用到了 B 树。
在 MySQL 的 InnoDB 存储引擎一次 IO 会读取的一页(默认一页 16K)的数据量,而二叉树一次 IO 有效数据量只有 16 字节,空间利用率极低。为了最大化利用一次 IO 空间,一个简单的想法是在每个节点存储多个元素,在每个节点尽可能多的存储数据。每个节点可以存储 1000 个索引(16k/16=1000),这样就将二叉树改造成了多叉树,通过增加树的叉树,将树从高瘦变为矮胖。构建 1 百万条数据,树的高度只需要 2 层就可以(1000*1000=1 百万),也就是说只需要 2 次磁盘 IO 就可以查询到数据。磁盘 IO 次数变少了,查询数据的效率也就提高了。
B 树也叫 B- 树,一颗 m 阶(m 表示这棵树最多有多少个分叉)的 B 树。
特点是:
-
每个非叶子节点并且非根节点最少有 m/2 个(向上取整),即内部节点的子节点个数最少也有 m/2 个。
-
根节点至少有两个子节点,每个内节点(非叶子节点就是内节点)最多有 m 个分叉。
-
B 树的所有节点都存储数据,一个节点包含多个元素,比如健值和数据,节点中的健值从小到大排序。
-
叶子节点都在同一层,高度一致并且它们之间没有指针相连。
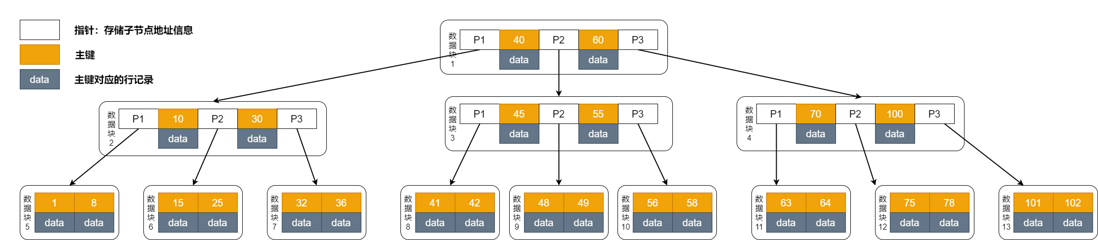
3 阶的 B 树结构如下图所示:
(1)等值查询
在这样的结构下我们找值等于 48 的数据,还是使用二分查找法。它的查询路径是这样的:数据库1->数据块3->数据块9。
一共经过三次磁盘 IO,而同样数据量情况下,用平衡二叉树存储的树高肯定是更高的。它的 IO 次数显然是更高的。所以说 B 树其实是加快了查询效率。
(2)范围查询
不知道大家注意到没有?
B 树的叶子节点,并没有指针相连。
意味着如果是范围查询,比如我查 41~ 58 的数据。
首先,二分查找法访问:数据块1->数据块3->数据块9,找到 41;然后再回去从根节点遍历:数据块1->数据块3->数据块10,找到 58,一共经历了 6 次 IO 查询才算是完成,这样查询的效率就慢了很多。
它还存在以下问题:
-
叶子节点无指针相连,所以范围查询增加了磁盘 IO 次数,降低了查询效率。
-
如果 data 存储的是行记录,行的大小随着列数的增多,所占空间会变大。这时,一个页中可存储的数据量就会变少,树相应就会变高,磁盘 IO 次数就会变大。
所以说,B 树还有优化的空间。
B+ 树
B+ 树其实是从 B 树衍生过来的。
它与 B 树有两个区别:
-
B+ 树的非叶子节点不存放数据,只存放健值。
-
B + 树的叶子节点之间存在双向指针相连,而且是双向有序链表
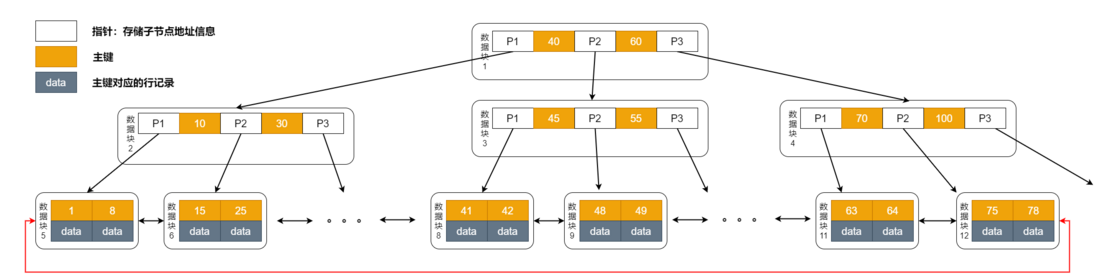
它的数据结构如下图所示:
由上图得知,B+ 树的数据都存放在叶子节点上。所以每次查询我们都需要检索到叶子节点才能把数据查出来。
有人说了,那这不变慢了吗?
B 树不一定要检索到叶子节点呀。
其实不然,因为 B+ 的非叶子节点不再存储数据。所以它可以存更多的索引,也即理论上 B+ 树的树高会比 B 树更低。
从这个角度来说,与其为了非叶子结点上能存储值而选择 B 树,倒不如选择 B+ 树,降低树高。
我们通过分析来看看 B+ 树靠不靠谱。
(1)等值查询
在这样的结构下我们找值等于 48 的数据,还是使用二分查找法。它的查询路径是这样的:数据块1->数据块3->数据块9。一共经过三次磁盘 IO,这没毛病。
(2)范围查询
比如我查 41~ 49 的数据。首先二分查找访问:数据库1->数据块3->数据块8。一样经过了三次磁盘 IO,找到 41 缓存到结果集。
但由于叶子节点是个双向有序链表,这个时候只需要往后走。将 49 所在的数据块 9 加载到内存遍历,找到 49,查询结束,只走了 4 次磁盘 IO。
这里可以看出对于范围查询来说,相比于 B 树要走一遍老路,B+ 树就显得高效很多。
所以,B+ 树中等值和范围查询都支持快速查。这样 MySQL 就选择了 B+ 树作为索引的内存模型。
拓展阅读
Mongo 为什么 MongoDB 使用 B-Tree,MySQL 使用 B+ Tree ?