KMP 算法
定义
Knuth-Morris-Pratt 字符串查找算法,简称为 “KMP算法”,常用于在一个文本串S内查找一个模式串P 的出现位置,这个算法由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表,故取这3人的姓氏命名此算法。
算法流程
下面先直接给出KMP的算法流程(如果感到一点点不适,没关系,坚持下,稍后会有具体步骤及解释,越往后看越会柳暗花明☺):
假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置
1. 如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++,继续匹配下一个字符;
2. 如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。
3. 换言之,当匹配失败时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的next 值(next 数组的求解会在下文的3.3.3节中详细阐述),即移动的实际位数为:j - next[j],且此值大于等于1。
很快,你也会意识到next 数组各值的含义:代表当前字符之前的字符串中,有多大长度的相同前缀后缀。
例如如果next [j] = k,代表j 之前的字符串中有最大长度为k 的相同前缀后缀。
此也意味着在某个字符失配时,该字符对应的next 值会告诉你下一步匹配中,模式串应该跳到哪个位置(跳到next [j] 的位置)。如果next [j] 等于0或-1,则跳到模式串的开头字符,若 next[j] = k && k > 0,代表下次匹配跳到j 之前的某个字符,而不是跳到开头,且具体跳过了 k 个字符。
PMT 是什么
有些算法,适合从它产生的动机,如何设计与解决问题这样正向地去介绍。
但KMP算法真的不适合这样去学。最好的办法是先搞清楚它所用的数据结构是什么,再搞清楚怎么用,最后为什么的问题就会有恍然大悟的感觉。
我试着从这个思路再介绍一下。大家只需要记住一点,PMT是什么东西。然后自己临时推这个算法也是能推出来的,完全不需要死记硬背。
KMP算法的核心,是一个被称为部分匹配表(Partial Match Table)的数组。
觉得理解KMP的最大障碍就是很多人在看了很多关于KMP的文章之后,仍然搞不懂PMT中的值代表了什么意思。
PMT 简介
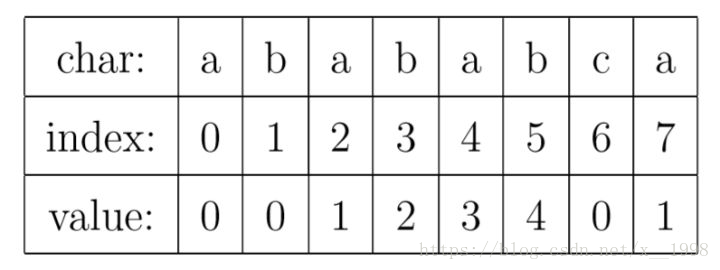
这里我们抛开所有的枝枝蔓蔓,先来解释一下这个数据到底是什么。对于字符串“abababca”,它的PMT如下表所示:
就像例子中所示的,如果待匹配的模式字符串有8个字符,那么PMT就会有8个值。
前缀
我先解释一下字符串的前缀和后缀。如果字符串A和B,存在A=BS,其中S是任意的非空字符串,那就称B为A的前缀。
例如,”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”},我们把所有前缀组成的集合,称为字符串的前缀集合。
后缀
同样可以定义后缀A=SB, 其中S是任意的非空字符串,那就称B为A的后缀。
例如,”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”},然后把所有后缀组成的集合,称为字符串的后缀集合。
要注意的是,字符串本身并不是自己的后缀。
有了这个定义,就可以说明PMT中的值的意义了。PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。
例如,对于”aba”,它的前缀集合为{”a”, ”ab”},后缀 集合为{”ba”, ”a”}。两个集合的交集为{”a”},那么长度最长的元素就是字符串”a”了,长 度为1,所以对于”aba”而言,它在PMT表中对应的值就是1。再比如,对于字符串”ababa”,它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”},它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}, 两个集合的交集为{”a”, ”aba”},其中最长的元素为”aba”,长度为3。
如何加速查找
好了,解释清楚这个表是什么之后,我们再来看如何使用这个表来加速字符串的查找,以及这样用的道理是什么。
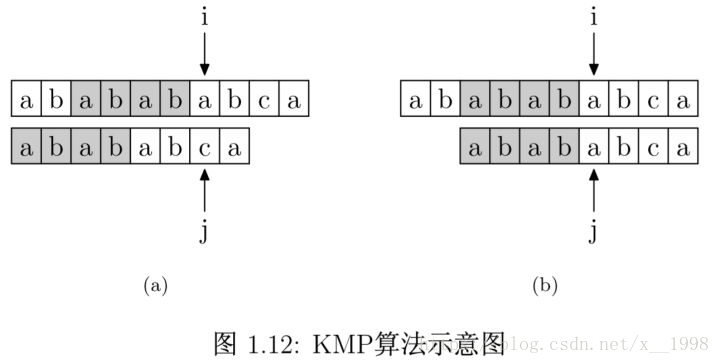
如图 1.12 所示,要在主字符串”ababababca”中查找模式字符串”abababca”。
如果在 j 处字符不匹配,那么由于前边所说的模式字符串 PMT 的性质,主字符串中 i 指针之前的 PMT[j −1] 位就一定与模式字符串的第 0 位至第 PMT[j−1] 位是相同的。这是因为主字符串在 i 位失配,也就意味着主字符串从 i−j 到 i 这一段是与模式字符串的 0 到 j 这一段是完全相同的。
而我们上面也解释了,模式字符串从 0 到 j−1 ,在这个例子中就是”ababab”,其前缀集合与后缀集合的交集的最长元素为”abab”, 长度为4。所以就可以断言,主字符串中i指针之前的 4 位一定与模式字符串的第0位至第 4 位是相同的,即长度为 4 的后缀与前缀相同。这样一来,我们就可以将这些字符段的比较省略掉。具体的做法是,保持i指针不动,然后将j指针指向模式字符串的PMT[j −1]位即可。
简言之,以图中的例子来说,在 i 处失配,那么主字符串和模式字符串的前边6位就是相同的。
又因为模式字符串的前6位,它的前4位前缀和后4位后缀是相同的,所以我们推知主字符串i之前的4位和模式字符串开头的4位是相同的。就是图中的灰色部分。那这部分就不用再比较了。
有了上面的思路,我们就可以使用PMT加速字符串的查找了。
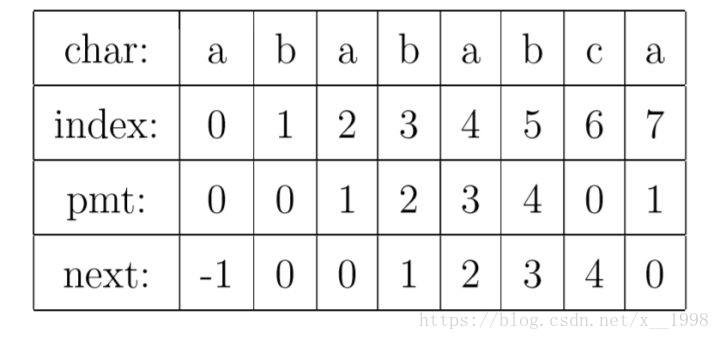
我们看到如果是在 j 位 失配,那么影响 j 指针回溯的位置的其实是第 j −1 位的 PMT 值,所以为了编程的方便, 我们不直接使用PMT数组,而是将PMT数组向后偏移一位。我们把新得到的这个数组称为next数组。下面给出根据next数组进行字符串匹配加速的字符串匹配程序。其中要注意的一个技巧是,在把PMT进行向右偏移时,第0位的值,我们将其设成了-1,这只是为了编程的方便,并没有其他的意义。
在本节的例子中,next数组如下表所示。
C 语言实现
int KMP(char * t, char * p)
{
int i = 0;
int j = 0;
while (i < strlen(t) && j < strlen(p))
{
if (j == -1 || t[i] == p[j])
{
i++;
j++;
}
else
j = next[j];
}
if (j == strlen(p))
return i - j;
else
return -1;
}
好了,讲到这里,其实KMP算法的主体就已经讲解完了。你会发现,其实KMP算法的动机是很简单的,解决的方案也很简单。远没有很多教材和算法书里所讲的那么乱七八糟,只要搞明白了PMT的意义,其实整个算法都迎刃而解。
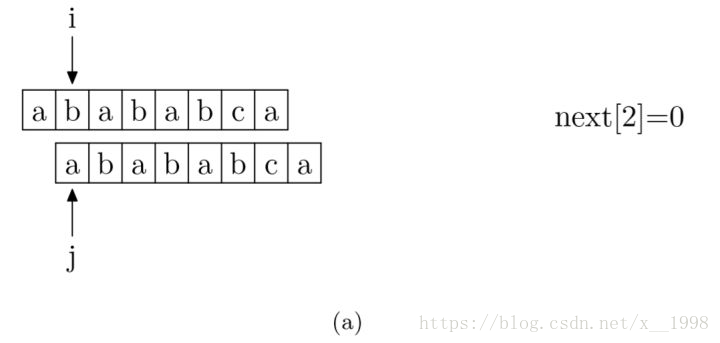
现在,我们再看一下如何编程快速求得next数组。其实,求next数组的过程完全可以看成字符串匹配的过程,即以模式字符串为主字符串,以模式字符串的前缀为目标字符串,一旦字符串匹配成功,那么当前的next值就是匹配成功的字符串的长度。
具体来说,就是从模式字符串的第一位(注意,不包括第0位)开始对自身进行匹配运算。
在任一位置,能匹配的最长长度就是当前位置的next值。
如下图所示。
获取 next 数组代码
void getNext(char * p, int * next)
{
next[0] = -1;
int i = 0, j = -1;
while (i < strlen(p))
{
if (j == -1 || p[i] == p[j])
{
++i;
++j;
next[i] = j;
}
else
j = next[j];
}
}
BM算法
KMP的匹配是从模式串的开头开始匹配的,而1977年,德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授发明了一种新的字符串匹配算法:
Boyer-Moore算法,简称BM算法。
该算法从模式串的尾部开始匹配,且拥有在最坏情况下O(N)的时间复杂度。在实践中,比KMP算法的实际效能高。
BM算法定义了两个规则:
坏字符规则:当文本串中的某个字符跟模式串的某个字符不匹配时,我们称文本串中的这个失配字符为坏字符,此时模式串需要向右移动,
移动的位数 = 坏字符在模式串中的位置 - 坏字符在模式串中最右出现的位置。
此外,如果”坏字符”不包含在模式串之中,则最右出现位置为-1。
好后缀规则:当字符失配时,后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串上一次出现的位置,且如果好后缀在模式串中没有再次出现,则为-1。
扩展2:Sunday算法
上文中,我们已经介绍了KMP算法和BM算法,这两个算法在最坏情况下均具有线性的查找时间。
但实际上,KMP算法并不比最简单的c库函数strstr()快多少,而BM算法虽然通常比KMP算法快,但BM算法也还不是现有字符串查找算法中最快的算法,本文最后再介绍一种比BM算法更快的查找算法即Sunday算法。
Sunday算法由Daniel M.Sunday在1990年提出,它的思想跟BM算法很相似:
只不过Sunday算法是从前往后匹配,在匹配失败时关注的是文本串中参加匹配的最末位字符的下一位字符。 如果该字符没有在模式串中出现则直接跳过,即移动位数 = 匹配串长度 + 1; 否则,其移动位数 = 模式串中最右端的该字符到末尾的距离+1。 下面举个例子说明下Sunday算法。假定现在要在文本串”substring searching algorithm”中查找模式串”search”。
1、 刚开始时,把模式串与文本串左边对齐:
substring searching algorithm
search
^
2、结果发现在第2个字符处发现不匹配,不匹配时关注文本串中参加匹配的最末位字符的下一位字符,即标粗的字符 i,因为模式串search中并不存在i,所以模式串直接跳过一大片,向右移动位数 = 匹配串长度 + 1 = 6 + 1 = 7,从 i 之后的那个字符(即字符n)开始下一步的匹配,如下图:
substring searching algorithm
search
^
3、结果第一个字符就不匹配,再看文本串中参加匹配的最末位字符的下一位字符,是’r’,它出现在模式串中的倒数第3位,于是把模式串向右移动3位(r 到模式串末尾的距离 + 1 = 2 + 1 =3),使两个’r’对齐,如下:
substring searching algorithm
search
^
4、匹配成功。
回顾整个过程,我们只移动了两次模式串就找到了匹配位置,缘于Sunday算法每一步的移动量都比较大,效率很高。