感知机
PLA 全称是 Perceptron Linear Algorithm,即线性感知机算法,属于一种最简单的感知机(Perceptron)模型。
感知机模型是机器学习二分类问题中的一个非常简单的模型。
核心思想
它的思想很简单,就是在一个二维空间中寻找一条直线将红点和蓝点分开(图1),类比到高维空间中,感知机模型尝试寻找一个超平面,将所有二元类别分开(图2)。


不可分的场景
如果我们找不到这么一条直线的话怎么办?找不到的话那就意味着类别线性不可分(图3),也就意味着感知机模型不适合你的数据的分类。
使用感知机一个最大的前提,就是数据是线性可分的。

基本结构
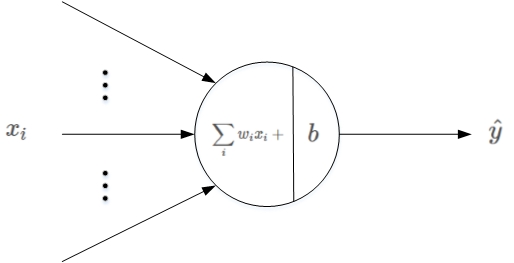
它的基本结构如下图所示:
其中,xi是输入,wi表示权重系数,b表示偏移常数。
线性输出
感知机的线性输出为:
scores=∑i~N wi*xi+b
为了简化计算,通常我们将b作为权重系数的一个维度,即w0。同时,将输入x扩展一个维度,为1。
这样,上式简化为:
scores=∑i~N+1 wi*xi
上面的和就是一个线性计算,然后可以和阈值比较,从而判定具体的分类。
阈值比较
scores 是感知机的输出,接下来就要对 scores 进行判断:
(1)若 scores≥0 ,则y^=1(正类)
(2)若 scores<0,则y^=−1(负类)
PLA 理论解释
感知机算法的原始形式
这里,我们直接给出《统计学习方法》中的原始算法。

理论解释
对于二分类问题,可以使用感知机模型来解决。
PLA的基本原理就是逐点修正,首先在超平面上随意取一条分类面,统计分类错误的点;然后随机对某个错误点就行修正,即变换直线的位置,使该错误点得以修正;接着再随机选择一个错误点进行纠正,分类面不断变化,直到所有的点都完全分类正确了,就得到了最佳的分类面。
例子
利用二维平面例子来进行解释,第一种情况是错误地将正样本(y=1)分类为负样本(y=-1)。
此时,wx < 0,即 w 与 x 的夹角大于90度,分类线 l 的两侧。
修正的方法是让夹角变小,修正 w 值,使二者位于直线同侧:
w:=w+x=w+yx
修正过程示意图如下所示:

第二种情况是错误地将负样本(y=-1)分类为正样本(y=1)。
此时,wx>0,即w与x的夹角小于90度,分类线l的同一侧。
修正的方法是让夹角变大,修正w值,使二者位于直线两侧:
w:=w−x=w+yx
修正过程示意图如下所示:

经过两种情况分析,我们发现PLA每次w的更新表达式都是一样的:w:=w+yx。
掌握了每次w的优化表达式,那么PLA就能不断地将所有错误的分类样本纠正并分类正确。
算法实现
数据准备
我们首先准备好一个已经做好分类的 csv 文件。
https://gitee.com/houbinbin/ai-data/blob/master/pla/data/data1.csv
大概内容如下:
...
5.1,3,1
5.7,4.1,1
5.1,1.4,-1
4.9,1.4,-1
...
你可以理解为这是一个 2 个维度的数据,最后一个数字代表是正,还是负。
数据导入
我们使用 jupyter notebook 进行编码,首先导入这个 csv 文件。
import numpy as np
import pandas as pd
data = pd.read_csv('D:\\_data\\ai-data\\pla\\data1.csv', header=None)
# 样本输入,维度(100,2)
x = data.iloc[:,:2].values
# 样本输出,维度(100,)
y = data.iloc[:,2].values
D:\\_data\\ai-data\\pla\\data1.csv 是这个 csv 在我本地的路径。
x 对应的就是前面的两个维度值:
array([[7. , 4.7],
[6.4, 4.5],
...
[4.8, 1.4],
[5.1, 1.6],
[4.6, 1.4],
[5.3, 1.5],
[5. , 1.4]])
y 对应的是最后的分类值:
array([ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
...
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
dtype=int64)
数据分类与可视化
还是那句话,一图盛千言。
我们把数据可视化表示出来。
import matplotlib.pyplot as plt
# 可视化
plt.scatter(x[:50, 0], x[:50, 1], color='blue', marker='o', label='Positive')
plt.scatter(x[50:, 0], x[50:, 1], color='red', marker='x', label='Negative')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(loc = 'upper left')
plt.title('Original Data')
plt.show()
效果如下图:

二维的数据,对应的坐标上刚好就是一个平面上的点。
接下来,我们就需要找到一个直线,将这个平面一分为二。
特征归一化(normalization)介绍
归一化的作用
两个特征在数值上差异巨大,如果直接将该样本送入训练,则代价函数的轮廓会是“扁长的”,在找到最优解前,梯度下降的过程不仅是曲折的,也是非常耗时的。
归一化的方法
(1)线性比例变换
yi = xi / max(x)
将原始数据线性化的方法转换到[0 1]的范围,该方法实现对原始数据的等比例缩放。
通过利用变量取值的最大值和最小值(或者最大值)将原始数据转换为界于某一特定范围的数据,从而消除量纲和数量级影响,改变变量在分析中的权重来解决不同度量的问题。
由于极值化方法在对变量无量纲化过程中仅仅与该变量的最大值和最小值这两个极端值有关,而与其他取值无关,这使得该方法在改变各变量权重时过分依赖两个极端取值。
(2)极差变换法
yi = (xi - min(x)) / (max(x)-min(x))
(3)Z-score standardization
yi = (xi - μ) / σ
其中,μ是特征均值,σ是特征标准差。
在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,(Z-score standardization)表现更好。
数据归一化
这里我们使用 z-score 的方法。
# 归一化
# 均值
u = np.mean(x, axis=0)
# 方差
v = np.std(x, axis=0)
x = (x - u) / v
# 作图
plt.scatter(x[:50, 0], x[:50, 1], color='blue', marker='o', label='Positive')
plt.scatter(x[50:, 0], x[50:, 1], color='red', marker='x', label='Negative')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(loc = 'upper left')
plt.title('Normalization data')
plt.show()
效果如下:

数据的范围 x/y 轴都被转换到了固定的范围内。
直线初始化
显示初始化直线位置:
# 初始化直线
# x加上偏置项
x = np.hstack((np.ones((x.shape[0],1)), x))
# 权重初始化
w = np.random.randn(3,1)
# 直线第一个坐标(x1,y1)
x1 = -2
y1 = -1 / w[2] * (w[0] * 1 + w[1] * x1)
# 直线第二个坐标(x2,y2)
x2 = 2
y2 = -1 / w[2] * (w[0] * 1 + w[1] * x2)
plt.plot([x1,x2], [y1,y2],'r')
plt.show()
效果如下:

由上图可见,一般随机生成的分类线,错误率较高。
numpy 方法补充
我们补一下这里用到的 numpy 方法。
- shape
shape 函数是numpy.core.fromnumeric中的函数,它的功能是查看矩阵或者数组的维数。
x.shape[0] 是 100 维度。
- ones
返回一个指定形状和数据类型的新数组,并且数组中的值都为1。
np.ones((x.shape[0],1) 实际上返回的是一个 100 个元素都是 1 的数组。
- hstack
hstack表示轴1合并。
hstack的字母h来自于horizontal,表示两个数组是水平的,hstack((a,b))将把b排在a的右边的意思。
print(np.hstack([[1,2],[3]]))
# [1,2,3]
所以 np.hstack((np.ones((x.shape[0],1)), x)) 是为了实现前面说的:为了简化计算,通常我们将b作为权重系数的一个维度,即w0。同时,将输入x扩展一个维度,为1。
- random.randn
numpy.random.randn(d0,d1,…,dn)
randn函数返回一个或一组样本,具有标准正态分布。dn表格每个维度。
所以 w 是一个 3 维的随机数:
array([[0.64171487],
[0.74705545],
[0.66654185]])
只所以是 3 维,是因为刚好和扩充了 1 维的 x 刚好对应。
计算 scores
接下来,计算scores,得分函数与阈值0做比较,大于零则y^=1,小于零则y^=−1
s = np.dot(x, w)
y_pred = np.ones_like(y) # 预测输出初始化
loc_n = np.where(s < 0)[0] # 小于零索引下标
y_pred[loc_n] = -1
接着,从分类错误的样本中选择一个,使用PLA更新权重系数w。
# 第一个分类错误的点
t = np.where(y != y_pred)[0][0]
# 更新权重w
w += y[t] * x[t, :].reshape((3,1))
数组方法简介
x[t, :] 表示裁剪数组,从 t 到最后。
比如 x 的第一行是 [1. , 2.39474331, 1.27506221]
那么,x[0, :] 就是 array([1. , 2.39474331, 1.27506221])
x[0,:].reshape((3,1)) 就是把 3*1 转换为 3 行,1列的矩阵:
array([[1. ],
[2.39474331],
[1.27506221]])
这样 y[t] * x[t, :].reshape((3,1)) 才能得到一个 3 * 1 的矩阵:
y[0] * x[0,:].reshape((3,1))
=
array([[1. ],
[2.39474331],
[1.27506221]])
numpy 方法说明
- dot
np.dot(x, w) 实际上就是矩阵 x 与矩阵 w 的乘积。
矩阵乘法此处不做展开,感兴趣的小伙伴可以自己查一下数学资料。
- ones_like
返回与指定数组具有相同形状和数据类型的数组,并且数组中的值都为1。
这里实际上 np.ones_like(y) 返回的是一个 100 维的数组,值都是1。
- where(condition)
只有条件 (condition),没有x和y,则输出满足条件 (即非0) 元素的坐标 (等价于numpy.nonzero)。
这里的坐标以tuple的形式给出,通常原数组有多少维,输出的tuple中就包含几个数组,分别对应符合条件元素的各维坐标。
loc_n = np.where(s < 0)[0] # 小于零索引下标
y_pred[loc_n] = -1 # 把矩阵乘积 wi*xi 小于0 的位置,设置为 -1
迭代更新训练
更新权重w是个迭代过程,只要存在分类错误的样本,就不断进行更新,直至所有的样本都分类正确。
(注意,前提是正负样本完全可分)
for i in range(100):
s = np.dot(x, w)
y_pred = np.ones_like(y)
loc_n = np.where(s < 0)[0]
y_pred[loc_n] = -1
num_fault = len(np.where(y != y_pred)[0])
print('第%2d次更新,分类错误的点个数:%2d' % (i, num_fault))
if num_fault == 0:
break
else:
t = np.where(y != y_pred)[0][0]
w += y[t] * x[t, :].reshape((3,1))
迭代完毕后,得到更新后的权重系数 w ,绘制此时的分类直线是什么样子。
# 直线第一个坐标(x1,y1)
x1 = -2
y1 = -1 / w[2] * (w[0] * 1 + w[1] * x1)
# 直线第二个坐标(x2,y2)
x2 = 2
y2 = -1 / w[2] * (w[0] * 1 + w[1] * x2)
# 作图
plt.scatter(x[:50, 1], x[:50, 2], color='blue', marker='o', label='Positive')
plt.scatter(x[50:, 1], x[50:, 2], color='red', marker='x', label='Negative')
plt.plot([x1,x2], [y1,y2],'r')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(loc = 'upper left')
plt.show()
x,y 的问题
# 直线第一个坐标(x1,y1)
x1 = -2
y1 = -1 / w[2] * (w[0] * 1 + w[1] * x1)
# 直线第二个坐标(x2,y2)
x2 = 2
y2 = -1 / w[2] * (w[0] * 1 + w[1] * x2)
这个不知道你看起来会不会觉得奇怪。
这个实际上是根据:
w[0]*1 + w[1]*x1 + w[2]*y1=0
这个公式简单推导出来的。
完整的代码
- PLA.py
# PLA算法
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 数据读取
data = pd.read_csv('D:\\_data\\ai-data\\pla\\data1.csv', header=None)
# 样本输入,维度(100,2)
x = data.iloc[:,:2].values
# 样本输出,维度(100,)
y = data.iloc[:,2].values
# 数据归一化
u = np.mean(x, axis=0)
v = np.std(x, axis=0)
x = (x - u) / v
# 直线初始化
# x加上偏置项
x = np.hstack((np.ones((x.shape[0],1)), x))
# 权重初始化
w = np.random.randn(3,1)
# 迭代更新
for i in range(100):
s = np.dot(x, w)
y_pred = np.ones_like(y)
loc_n = np.where(s < 0)[0]
y_pred[loc_n] = -1
num_fault = len(np.where(y != y_pred)[0])
print('第%2d次更新,分类错误的点个数:%2d' % (i, num_fault))
if num_fault == 0:
break
else:
t = np.where(y != y_pred)[0][0]
w += y[t] * x[t, :].reshape((3,1))
# 直线第一个坐标(x1,y1)
x1 = -2
y1 = -1 / w[2] * (w[0] * 1 + w[1] * x1)
# 直线第二个坐标(x2,y2)
x2 = 2
y2 = -1 / w[2] * (w[0] * 1 + w[1] * x2)
# 作图
plt.scatter(x[:50, 1], x[:50, 2], color='blue', marker='o', label='Positive')
plt.scatter(x[50:, 1], x[50:, 2], color='red', marker='x', label='Negative')
plt.plot([x1,x2], [y1,y2],'r')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(loc = 'upper left')
plt.show()
输出如下:
第 0次更新,分类错误的点个数: 3
第 1次更新,分类错误的点个数:23
第 2次更新,分类错误的点个数: 2
第 3次更新,分类错误的点个数: 0

其实,PLA算法的效率还算不错,只需要数次更新就能找到一条能将所有样本完全分类正确的分类线。
所以得出结论,对于正负样本线性可分的情况,PLA能够在有限次迭代后得到正确的分类直线。
总结与疑问
本文导入的数据本身就是线性可分的,可以使用 PLA 来得到分类直线。
但是,如果数据不是线性可分,即找不到一条直线能够将所有的正负样本完全分类正确,这种情况下,似乎 PLA 会永远更新迭代下去,却找不到正确的分类线。
对于线性不可分的情况,该如何使用PLA算法呢?
参考资料
《统计学习方法》