所有的路径
题目
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
输入:
1
/
2 3
5
输出: [“1->2->5”, “1->3”]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
思路
最直观的方法是使用深度优先搜索。
在深度优先搜索遍历二叉树时,我们需要考虑当前的节点以及它的孩子节点。
(1)如果当前节点不是叶子节点,则在当前的路径末尾添加该节点,并继续递归遍历该节点的每一个孩子节点。
(2)如果当前节点是叶子节点,则在当前路径末尾添加该节点后我们就得到了一条从根节点到叶子节点的路径,将该路径加入到答案即可。
如此,当遍历完整棵二叉树以后我们就得到了所有从根节点到叶子节点的路径。
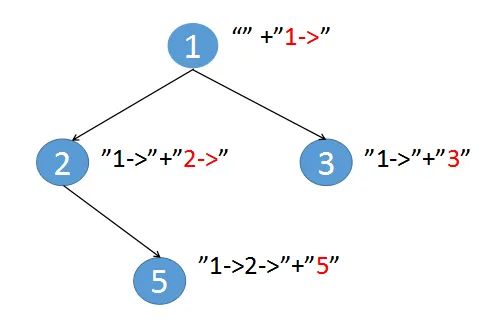
完整的過程如下:
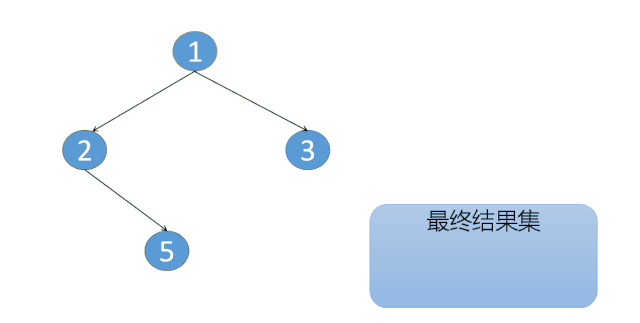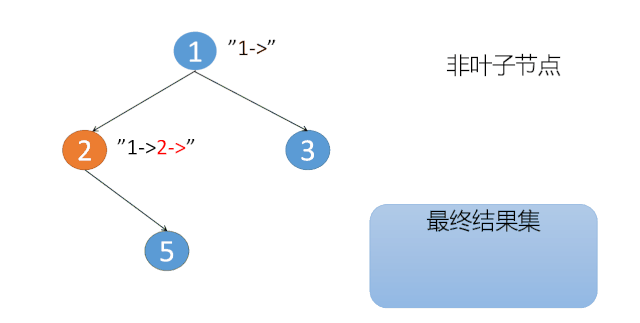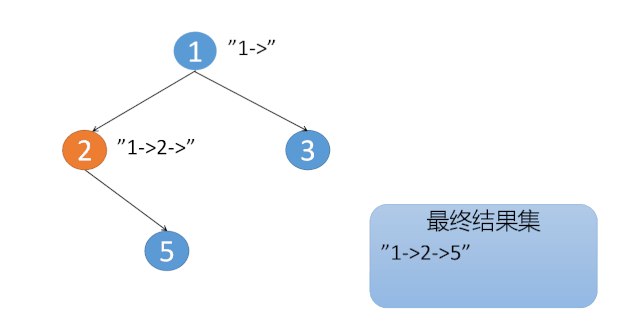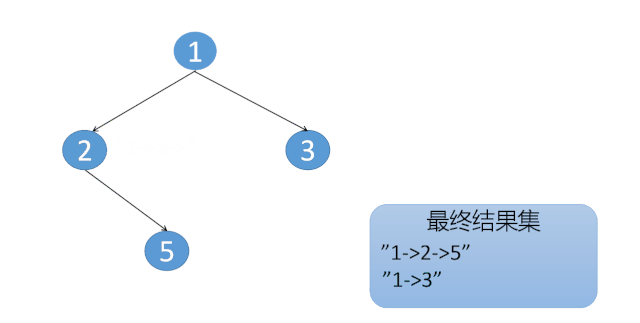
java 实现
public List<String> binaryTreePaths(TreeNode root) {
List<String> results = new ArrayList<>();
binaryTreePaths(results, new StringBuilder(), root);
return results;
}
private void binaryTreePaths(List<String> results, StringBuilder builder, TreeNode root) {
if(root == null) {
return;
}
builder.append(root.val);
// 叶子节点
if(root.left == null && root.right == null) {
results.add(builder.toString());
}
builder.append("->");
// 左右子树
binaryTreePaths(results, new StringBuilder(builder), root.left);
binaryTreePaths(results, new StringBuilder(builder), root.right);
}
效果:
Runtime: 1 ms, faster than 99.81% of Java online submissions for Binary Tree Paths.
Memory Usage: 39.2 MB, less than 58.21% of Java online submissions for Binary Tree Paths.
复杂度
时间复杂度:O(N^2)
空间复杂度:O(N^2)
路径总和的路径
题目
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
- 示例 2:

输入:root = [1,2,3], targetSum = 5
输出:[]
- 示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
提示:
树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
思路
有了前面一道题的铺垫,我们可以很自然的想到下面的解法:
(1)找到所有路径列表
(2)遍历路径列表,找到符合总和的路径。
java 实现
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> allPaths = new ArrayList<>();
getAllPathSum(allPaths, new ArrayList<>(), root);
// 筛选符合条件的列表
List<List<Integer>> results = new ArrayList<>();
for(List<Integer> all : allPaths) {
if(isTargetList(all, targetSum)) {
results.add(all);
}
}
return results;
}
private void getAllPathSum(List<List<Integer>> allPaths, List<Integer> tempList, TreeNode root) {
if(root == null) {
return ;
}
tempList.add(root.val);
// 叶子
if(root.left == null && root.right == null) {
allPaths.add(tempList);
}
// 左右子树
getAllPathSum(allPaths, new ArrayList<>(tempList), root.left);
getAllPathSum(allPaths, new ArrayList<>(tempList), root.right);
}
实现和上面一题基本一致,其中判断是否符合条件的实现如下:
private boolean isTargetList(List<Integer> list, int target) {
if(list.size() == 0) {
return false;
}
int sum = 0;
for(Integer integer : list) {
sum += integer;
}
return target == sum;
}
效果:
Runtime: 3 ms, faster than 14.56% of Java online submissions for Path Sum II.
Memory Usage: 41.5 MB, less than 21.94% of Java online submissions for Path Sum II.
有点惨,那么应该怎么优化呢?
优化思路一:直接计算
我们实际上在遍历的时候,就可以计算出对应的和,而不应该在最后得到列表之后才去筛选。
为了计算总和,我们传入一个临时的 sum 变量,实现调整如下:
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> allPaths = new ArrayList<>();
getAllPathSum(allPaths, new ArrayList<>(), root, targetSum, 0);
return allPaths;
}
private void getAllPathSum(List<List<Integer>> allPaths, List<Integer> tempList,
TreeNode root, int targetSum, int currentSum) {
if(root == null) {
return ;
}
tempList.add(root.val);
currentSum += root.val;
// 叶子
if(root.left == null && root.right == null && targetSum == currentSum) {
allPaths.add(tempList);
}
// 左右子树
getAllPathSum(allPaths, new ArrayList<>(tempList), root.left, targetSum, currentSum);
getAllPathSum(allPaths, new ArrayList<>(tempList), root.right, targetSum, currentSum);
}
效果:
Runtime: 2 ms, faster than 35.52% of Java online submissions for Path Sum II.
Memory Usage: 41.8 MB, less than 13.36% of Java online submissions for Path Sum II.
虽然进步了一点,不过还是有点差强人意。
优化思路二:剪枝
老马能想到的第二个优化思路就是进行剪枝。
剪枝的思路:如果一个分支的和,已经大于 targetSum 值了,就没有必要执行了。
不过这只是一颗普通的二叉树,而且值有正有负,所以暂时放弃这个思路。
那么,到底还有什么优化空间呢?
优化思路三:数组创建
其实我们算法整体思路是没有毛病的,但是还是有太多的 ArrayList 的创建。
实际上是可以优化掉的:
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> allPaths = new ArrayList<>();
getAllPathSum(allPaths, new ArrayList<>(), root, targetSum, 0);
return allPaths;
}
private void getAllPathSum(List<List<Integer>> allPaths, List<Integer> tempList,
TreeNode root, int targetSum, int currentSum) {
if(root == null) {
return ;
}
tempList.add(root.val);
currentSum += root.val;
// 叶子
if(root.left == null && root.right == null && targetSum == currentSum) {
allPaths.add(new ArrayList<>(tempList));
}
// 左右子树
getAllPathSum(allPaths, tempList, root.left, targetSum, currentSum);
getAllPathSum(allPaths, tempList, root.right, targetSum, currentSum);
// 移除最后一个元素
tempList.remove(tempList.size()-1);
}
我们在存入结果的时候,统一新建列表。
每次迭代之后,移除最后一个元素,便于回溯。
效果:
Runtime: 1 ms, faster than 99.97% of Java online submissions for Path Sum II.
Memory Usage: 39.3 MB, less than 80.84% of Java online submissions for Path Sum II.
好的,这下还差不多。
是否包含路径总和
题目
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ,判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。
叶子节点 是指没有子节点的节点。
- 示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true
- 示例 2:

输入:root = [1,2,3], targetSum = 5 输出:false
- 示例 3:
输入:root = [1,2], targetSum = 0 输出:false
提示:
树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
思路
我们知道如何求一棵树的所有路径之后,计算符合目标的和也就比较简单了。
而且我们不需要关心所有的路径结果,如果有一个符合的,直接返回就行。
java 实现
public boolean hasPathSum(TreeNode root, int targetSum) {
return hasPathSum(new ArrayList<>(), root, targetSum, 0);
}
private boolean hasPathSum(List<Integer> tempList,
TreeNode root, int targetSum,
int currentSum) {
if(root == null) {
return false;
}
tempList.add(root.val);
currentSum += root.val;
// 叶子
if(root.left == null && root.right == null && targetSum == currentSum) {
return true;
}
// 左右子树
return hasPathSum(tempList, root.left, targetSum, currentSum)
||
hasPathSum(tempList, root.right, targetSum, currentSum);
}
效果:
Runtime: 0 ms, faster than 100.00% of Java online submissions for Path Sum.
Memory Usage: 38.9 MB, less than 69.04% of Java online submissions for Path Sum.
任意长度路径之和
题目
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
示例:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1
返回 3。和等于 8 的路径有:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
思路一:穷举
我们可以把这个问题拆分为两步:
(1)找到一棵树的所有路径
(2)遍历每一个路径,从前往后遍历,找到符合条件的结果。
当然,第二步是需要一定技巧的,应该是一个 dp 问题?
第一步实现如下:
public List<List<Integer>> allPathSums(TreeNode root) {
List<List<Integer>> allPaths = new ArrayList<>();
getAllPathSum(allPaths, new ArrayList<>(), root);
return allPaths;
}
private void getAllPathSum(List<List<Integer>> allPaths, List<Integer> tempList,
TreeNode root) {
if(root == null) {
return ;
}
tempList.add(root.val);
// 叶子
if(root.left == null && root.right == null) {
allPaths.add(new ArrayList<>(tempList));
}
// 左右子树
getAllPathSum(allPaths, tempList, root.left);
getAllPathSum(allPaths, tempList, root.right);
// 移除最后一个元素
tempList.remove(tempList.size()-1);
}
但是第二步就不行了,卡主了。
// 穷举
// 0 ... n-1,一个也算吗?
// 每个元素可以重复吗?
// 长度为1,尝试一遍?
// 长度为2,尝试一遍?
// ...
// 长度为n,尝试一遍?
private List<Integer> allList(List<Integer> list, int targetSum) {
List<Integer> results = new ArrayList<>();
return results;
}
这样的话,时间直接就炸了。
而且题目也比较坑,没有说元素是否会重复,我们还是换一种思路。
思路2:双递归法
题目要求 路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点) 。
这就要求我们只需要去求三部分即可:
-
以当前节点作为头结点的路径数量
-
以当前节点的左孩子作为头结点的路径数量
-
以当前节点的右孩子作为头结点啊路径数量
将这三部分之和作为最后结果即可。
最后的问题是:我们应该如何去求以当前节点作为头结点的路径的数量?
这里依旧是按照树的遍历方式模板,每到一个节点让sum-root.val,并判断 remain 是否为0,如果为零的话,则找到满足条件的一条路径。
java 实现
递归的解法就是这么神奇,不得不说,神用递归!
public int pathSum(TreeNode root, int sum) {
if(root == null){
return 0;
}
int result = countPath(root,sum);
int a = pathSum(root.left,sum);
int b = pathSum(root.right,sum);
return result+a+b;
}
public int countPath(TreeNode root,int sum){
if(root == null){
return 0;
}
sum = sum - root.val;
int result = sum == 0 ? 1:0;
return result + countPath(root.left,sum) + countPath(root.right,sum);
}
整体逻辑甚至只有两个:
(1)终止条件代码
if(root == null){
return 0;
}
(2)核心逻辑
sum 等于目标值:
sum = sum - root.val;
int result = sum == 0 ? 1:0;
效果
双递归是一种相对比较自然的实现,但是性能一般:
Runtime: 22 ms, faster than 25.58% of Java online submissions for Path Sum III.
Memory Usage: 39.2 MB, less than 29.40% of Java online submissions for Path Sum III.
前缀和
这里介绍一个比较优秀的解法:前缀和。
前缀和定义
一个节点的前缀和就是该节点到根之间的路径和。
拿下图解释:
节点4的前缀和为:1 + 2 + 4 = 7 节点8的前缀和:1 + 2 + 4 + 8 = 15 节点9的前缀和:1 + 2 + 5 + 9 = 17
1
/ \
2 3
/ \ \
4 5 6
/ \ \
7 8 9
与本题的关系
题目要求的是找出路径和等于给定数值的路径总数, 而:
两节点间的路径和 = 两节点的前缀和之差
举个例子:
1
/
2
/
3
/
4
假如题目给定数值为5
节点1的前缀和为: 1
节点3的前缀和为: 1 + 2 + 3 = 6
prefix(3) - prefix(1) == 5
所以 节点1 到 节点3 之间有一条符合要求的路径( 2 --> 3 )
理解了这个之后,问题就得以简化:
我们只用遍历整颗树一次,记录每个节点的前缀和,并查询该节点的祖先节点中符合条件的个数,将这个数量加到最终结果上。
HashMap存的是什么
HashMap的key是前缀和, value是该前缀和的节点数量,记录数量是因为有出现复数路径的可能。
拿图说明:
下图树中,前缀和为1的节点有两个: 1, 0
所以路径和为2的路径数就有两条: 0 –> 2, 2
1
/
0
/
2
恢复状态的意义
由于题目要求:路径方向必须是向下的(只能从父节点到子节点)
当我们讨论两个节点的前缀和差值时,有一个前提:一个节点必须是另一个节点的祖先节点。
换句话说,当我们把一个节点的前缀和信息更新到map里时,它应当只对其子节点们有效。
举个例子,下图中有两个值为2的节点(A, B)。
0
/ \
A:2 B:2
/ \ \
4 5 6
/ \ \
7 8 9
当我们遍历到最右方的节点6时,对于它来说,此时的前缀和为2的节点只该有B, 因为从A向下到不了节点6(A并不是节点6的祖先节点)。
如果我们不做状态恢复,当遍历右子树时,左子树中A的信息仍会保留在map中,那此时节点6就会认为A, B都是可追溯到的节点,从而产生错误。
状态恢复代码的作用就是: 在遍历完一个节点的所有子节点后,将其从map中除去。
java 实现
// key是前缀和, value是大小为key的前缀和出现的次数
Map<Integer, Integer> prefixMap;
int target;
public int pathSum(TreeNode root, int sum) {
prefixMap = new HashMap<>();
target = sum;
// 前缀和为0的一条路径
prefixMap.put(0, 1);
return recur(root, 0);
}
private int recur(TreeNode node, int curSum) {
// 1.递归终止条件
if(node == null) {
return 0;
}
// 2.本层要做的事情
int res = 0;
// 当前路径上的和
curSum += node.val;
// 看看root到当前节点这条路上是否存在节点前缀和加target为currSum的路径
// 当前节点->root节点反推,有且仅有一条路径,如果此前有和为currSum-target,而当前的和又为currSum,两者的差就肯定为target了
// currSum-target相当于找路径的起点,起点的sum+target=currSum,当前点到起点的距离就是target
res += prefixMap.getOrDefault(curSum - target, 0);
prefixMap.put(curSum, prefixMap.getOrDefault(curSum, 0) + 1);
// 3.进入下一层
int left = recur(node.left, curSum);
int right = recur(node.right, curSum);
res = res + left + right;
// 4.回到本层,恢复状态,去除当前节点的前缀和数量
prefixMap.put(curSum, prefixMap.get(curSum) - 1);
return res;
}
效果
Runtime: 2 ms, faster than 100.00% of Java online submissions for Path Sum III.
Memory Usage: 38.8 MB, less than 61.97% of Java online submissions for Path Sum III.
复杂度
时间:O(N)
空间:O(N)
求根节点到叶节点数字之和
題目
https://leetcode-cn.com/problems/sum-root-to-leaf-numbers
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。 计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:

输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
示例 2:

输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
提示:
-
树中节点的数目在范围 [1, 1000] 内
-
0 <= Node.val <= 9
-
树的深度不超过 10
思路1
在前面我们学会获取二叉树的全路径之后,这一题就变得非常简单。
(1)获取全路径
(2)遍历列表,构建对应的数字,直接累加即可。
数字的构建方式,比如 1 2 3 4
实际上就是:
1 * 10^3 + 2 * 10^2 + 3 * 10^1 + 4 * 10^0
java 实现
编码也非常的简单:
public int sumNumbers(TreeNode root) {
List<List<Integer>> results = new ArrayList<>();
getAllPath(root, results, new ArrayList<>());
// 遍历构建
int sum = 0;
for(int i = 0; i < results.size(); i++) {
sum += calcInt(results.get(i));
}
return sum;
}
// 1 2 3 4 = 1 * 10^3 + 2*10^2 + 3*10 + 4;
private int calcInt(List<Integer> list) {
int sum = 0;
for(int i = 0; i < list.size(); i++) {
int pow = list.size() -1 - i;
sum += list.get(i) * Math.pow(10, pow);
}
return sum;
}
private void getAllPath(TreeNode node, List<List<Integer>> results,
List<Integer> tempList) {
if(node == null) {
return;
}
tempList.add(node.val);
if(node.left == null && node.right == null) {
results.add(tempList);
}
getAllPath(node.left, results, new ArrayList<>(tempList));
getAllPath(node.right, results, new ArrayList<>(tempList));
}
理所当然的 AC,不过一看效果:
Runtime: 1 ms, faster than 28.21% of Java online submissions for Sum Root to Leaf Numbers.
Memory Usage: 36.9 MB, less than 30.13% of Java online submissions for Sum Root to Leaf Numbers.
整个人都傻了,啥,性能怎么这么差?
所以到底别人的性能为啥这么好?
思路2
秉持着打不过就加入的心态,我学习了一下别人的解法思路。
发现有一个很大的问题,就是我们的计算过程没有任何的复用,所以产生了很多的浪费。
1
/ \
2 3
/\
4 5
比如对于 [1,2,4] 和 [1,2,5] 的两个分支计算,我们原来的方法全部是从头计算,实际上 1,2 这部分是可以复用的。
对于 [1,2,4] 的计算方式可以调整如下:
第一步:1
第二次:1*10 + 2
第三次:10 * (1*10 + 2) + 4
这种好处就是可以复用上一次的计算。
java 实现
private int sum = 0;
private int temp = 0;
public int sumNumbers(TreeNode root) {
calc(root);
return sum;
}
private void calc(TreeNode node) {
if(node == null) {
return;
}
temp = temp * 10 + node.val;
// 叶子
if(node.left == null && node.right == null) {
sum += temp;
}
// 递归子节点
calc(node.left);
calc(node.right);
// 返回上一层
temp /= 10;
}
效果:
Runtime: 0 ms, faster than 100.00% of Java online submissions for Sum Root to Leaf Numbers.
Memory Usage: 36.2 MB, less than 96.95% of Java online submissions for Sum Root to Leaf Numbers.
嗯,只能说是非常满意了~~
学无止境,学无止境。
小结
希望本文对你有帮助,如果有其他想法的话,也可以评论区和大家分享哦。
各位极客的点赞收藏转发,是老马持续写作的最大动力!
参考资料
https://leetcode.com/problems/binary-tree-paths/
