填充每个节点的下一个右侧节点指针
题目
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。
二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL
进阶:
- 你只能使用常量级额外空间。
使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
例子
示例:

输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
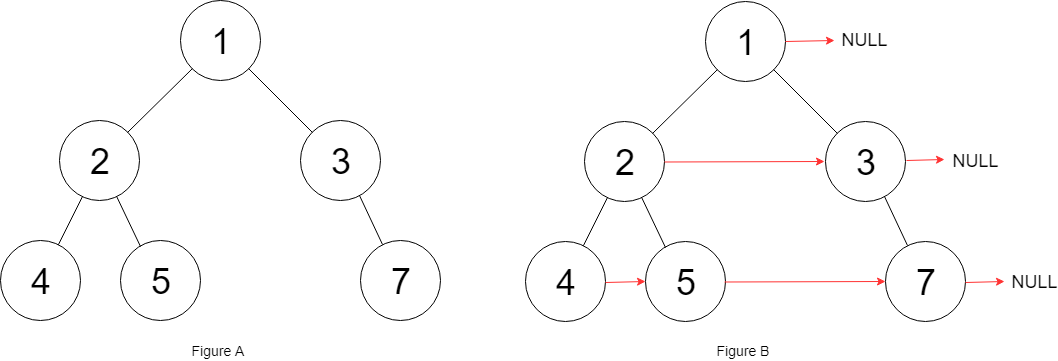
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
提示:
-
树中节点的数量少于 4096
-
-1000 <= node.val <= 1000
分析
老马看到这一题的时候,实际上是一点不慌的,因为前不久刚回顾了二叉树的遍历方式。
这一题就是在层序遍历的基础上,加了一点点变化。
因为节点本身新增了 next 指针,所以 left/right 指针是完全可以保持不变的。
目标:
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
拆解为两件事情:
(1)如果有右侧节点
在于层序遍历中,我们是从左往右遍历的。
所以需要保留上一个节点的信息,然后指向当前节点即可。
(2)如果没有右侧节点
如何判断有没有右侧节点呢?
实际上每一层的最后一个元素是没有右侧节点的。
问题就变成了如何如何判断节点是当前层的最后一个节点。老马相信很多聪明的小伙伴已经有答案了,没有的可以再读一遍题目。
没错,这是一颗完美二叉树,每个父节点都有两个子节点。
所以每一层的有多少个元素我们都是知道的: 1 2 4 8 …
java 实现
编码就变得非常简单了,我们在层序遍历的基础上稍作修改:
public Node connect(Node root) {
List<List<Node>> results = new ArrayList<>();
levelOrder(results, root, 0);
return root;
}
private void levelOrder(List<List<Node>> results, Node node, int level) {
if(node == null) {
return;
}
// 当前节点
// AVOID BOUND EX
if(results.size() <= level) {
results.add(new ArrayList<>());
}
List<Node> list = results.get(level);
// 如果列表不为空,把上一个 node 的 next 指向当前 Node
if(list.size() > 0) {
Node pre = list.get(list.size()-1);
pre.next = node;
}
// 当前层最后一个元素
int maxNum = (int) Math.pow(2, level);
if(list.size() == maxNum-1) {
node.next = null;
}
// 节点
list.add(node);
results.set(level, list);
// 左
levelOrder(results, node.left, level+1);
// 右
levelOrder(results, node.right, level+1);
}
效果:
Runtime: 1 ms, faster than 57.79% of Java online submissions for Populating Next Right Pointers in Each Node.
Memory Usage: 39.2 MB, less than 70.19% of Java online submissions for Populating Next Right Pointers in Each Node.
虽然实现了,可是性能比较差。
那么应该如何优化呢?
优化思路
那么问题来了,问题出在哪里了呢?
主要问题是我们浪费了大量的资源在列表的处理判断上,但是如果不这么做,还有其他方法吗?
答案是有的,让我们再看一下题目的要求。

实际上,我们原来是在遍历当前层的时候,进行链表的连接设置,其实还有一种方法,那就是,在遍历上一层的时候,把下一层从左到右链接起来。
假如我们访问第二行,可以按照下面的流程把第三行进行链接。


可以总结为 2 点:
(1)左子树
当前节点的左子树,直接 next 指向当前节点的右子树。
完美二叉树,左子树存在,则右子树必然存在。
(2)右子树
当前节点的右子树,分为两个场景。
如果当前节点.next 存在,则直接右子树指向 当前节点.next.left
否则,指向空。(每一层的末尾)
java 实现
递归时间其实非常简单:
public Node connect(Node root) {
connect(root, null);
return root;
}
private void connect(Node current, Node next) {
// 终止条件
if (current == null) {
return;
}
// 核心逻辑
current.next = next;
// 左=》右(当前节点,左子树=》右子树)
connect(current.left, current.right);
// 右子树,指向当前节点 next 的左子树,或者指向空
connect(current.right, current.next == null ? null : current.next.left);
}
效果:
Runtime: 0 ms, faster than 100.00% of Java online submissions for Populating Next Right Pointers in Each Node.
Memory Usage: 39.3 MB, less than 45.38% of Java online submissions for Populating Next Right Pointers in Each Node.
什么叫神用递归,这就叫神用递归。
填充每个节点的下一个右侧节点指针 II
题目
解决了上面的题目,我们稍微调整下条件。
给定一个二叉树
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
进阶:
你只能使用常量级额外空间。
使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
例子
输入:root = [1,2,3,4,5,null,7]
输出:[1,#,2,3,#,4,5,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),'#' 表示每层的末尾。
提示:
-
树中的节点数小于 6000
-
-100 <= node.val <= 100
思路 1
和上面类似,直接分成两步:
(1)层序遍历获取所有元素
(2)按照层级,依次设置 next 指向
java 实现
public Node connect(Node root) {
List<List<Node>> results = new ArrayList<>();
connect(results, root, 0);
// 设置 next
for(int i = 0; i < results.size(); i++) {
List<Node> list = results.get(i);
for(int j = 1; j < list.size(); j++) {
Node pre = list.get(j-1);
pre.next = list.get(j);
}
}
return root;
}
private void connect(List<List<Node>> results, Node node, int level) {
if (node == null) {
return;
}
// AVOID BOUND EX
if(results.size() <= level) {
results.add(new ArrayList<>());
}
List<Node> list = results.get(level);
if(list == null) {
list = new ArrayList<>();
}
list.add(node);
results.set(level, list);
connect(results, node.left, level+1);
connect(results, node.right, level+1);
}
效果:
Runtime: 1 ms, faster than 55.82% of Java online submissions for Populating Next Right Pointers in Each Node II.
Memory Usage: 38.7 MB, less than 50.24% of Java online submissions for Populating Next Right Pointers in Each Node II.
复杂度
时间:O(N)
空间:O(N)
思路 2
从根节点开始。
因为第 0 层只有一个节点,不需要处理。可以在上一层为下一层建立 next指针。
该方法最重要的一点是:位于第 x 层时为第 x+1 层建立 next 指针。
一旦完成这些连接操作,移至第 x+1 层为第 x+2 层建立 next 指针。
当遍历到某层节点时,该层节点的 next 指针已经建立。这样就不需要队列从而节省空间。
每次只要知道下一层的最左边的节点,就可以从该节点开始,像遍历链表一样遍历该层的所有节点。
java 实现
这种实现的优势就是空间复杂度为O(1)。
// 上一个节点
private Node pre = null;
// 下一层的开始节点
private Node nextStart = null;
public Node connect(Node root) {
Node start = root;
while (start != null) {
pre = null;
nextStart = null;
Node current = start;
while (current != null) {
// 处理下一层的 next 关系
handle(current.left);
handle(current.right);
// 移动当前层的位置
current = current.next;
}
// 下一层的开始节点
start = nextStart;
}
return root;
}
private void handle(Node current) {
if(current == null) {
return;
}
// 设置子节点层 pre.next = current
if (pre != null) {
pre.next = current;
}
// 更新 pre
pre = current;
// 设置下一层的开始节点(第一个非空的元素)
if (nextStart == null) {
nextStart = current;
}
}
效果:
Runtime: 0 ms, faster than 100.00% of Java online submissions for Populating Next Right Pointers in Each Node II.
Memory Usage: 38.9 MB, less than 29.02% of Java online submissions for Populating Next Right Pointers in Each Node II.
小结
希望本文对你有帮助,如果有其他想法的话,也可以评论区和大家分享哦。
各位极客的点赞收藏转发,是老马持续写作的最大动力!
参考资料
https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node/
