141. Linked List Cycle
描述
Given head, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer.
Internally, pos is used to denote the index of the node that tail’s next pointer is connected to. Note that pos is not passed as a parameter.
Return true if there is a cycle in the linked list. Otherwise, return false.
EX
Example 1:

Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
Example 2:

Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.
Example 3:
Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.
Constraints:
The number of the nodes in the list is in the range [0, 10^4].
-10^5 <= Node.val <= 10^5
pos is -1 or a valid index in the linked-list.
解题思路
第一感觉
这一题虽然难度标志为 easy,但是想不到方法实际上根本解不出来。
这里有几个点比较容易误解:
1)pos 我们在入参中没有,但是题目又说到这个,令人困惑。
2)node 节点我们能得到的只有 value 值,但是值并不是唯一的。所以循环看值是否重复,这是不可行的。
快慢指针
我们可以通过快慢指针的方式。
定义 fast/slow 两个指针,从头开始一起跑。
fast 一次走2步,slow 一次走1步。
如果后面发现二者又重合了,说明存在环。
java 解法
public boolean hasCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while (fast != null
&& fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if(fast == slow) {
return true;
}
}
return false;
}
解释上面一道题,主要是为了下面这道题做铺垫。
142. Linked List Cycle II
Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer.
Internally, pos is used to denote the index of the node that tail’s next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
EX
Example 1:

Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.
Example 2:

Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.
Example 3:
Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.
Constraints:
The number of the nodes in the list is in the range [0, 10^4].
-10^5 <= Node.val <= 10^5
pos is -1 or a valid index in the linked-list.
第一感觉
说实在的,这个问题主要分 2 步:
-
链表中是否存在环?
-
如何找到环开始的节点?
第一个问题,很好解决。那么,第二个问题呢?
其实这是一道数学题,这题难度虽然为 M,但是不理解还是很难解决。
我们来看一张图:
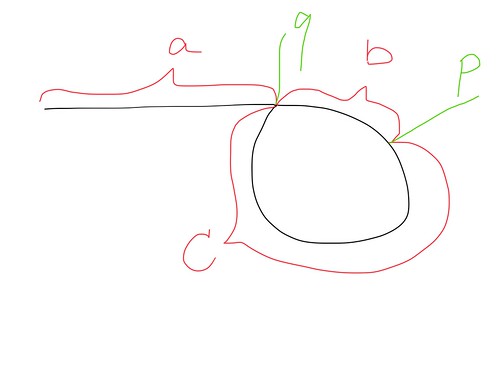
我们假设快慢指针在 p 点重逢。
q 点就是循环开始的节点,开始到 q 点的距离为 a
b 为 q 到 p 的距离
c 为 p 到 q 的距离。
那么快指针走的距离:a + 2b + c
慢指针走的距离:a + b
快指针因为移动的距离是慢指针的 2 倍,所以可以建立等式关系:a + 2b + c = 2 (a + b), 得到 c == a;
所以快慢指针在 p 点重合以后,我们在让 slow2 慢指针从头触发,slow1 指针从 p 点触发,二者速度一次一个节点,最后会在 q 点重合。重合的位置,刚好就是第一次出现环的位置。
java 实现
public ListNode detectCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
ListNode slow2 = head;
while (fast != null
&& fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if(fast == slow) {
// 此时,slow2 从头开始,slow 从重合点开始。
while (slow != slow2) {
slow = slow.next;
slow2 = slow2.next;
}
// 两个慢指针重合时,slow2 就在第一个环的节点上
return slow2;
}
}
return null;
}
参考资料
https://leetcode.com/problems/linked-list-cycle/
https://leetcode.com/problems/linked-list-cycle-ii/solutions/44774/java-o-1-space-solution-with-detailed-explanation/?orderBy=most_votes
