84. Largest Rectangle in Histogram
Given an array of integers heights representing the histogram’s bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.
EX
Example 1:

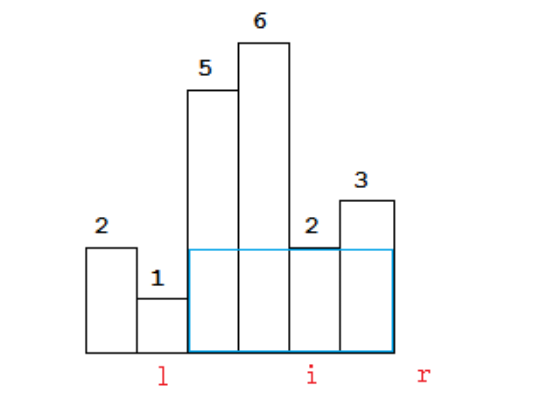
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.
Example 2:

Input: heights = [2,4]
Output: 4
Constraints:
1 <= heights.length <= 105 0 <= heights[i] <= 104
V1-暴力解法
思路
最简单的思路,就是直接遍历整个数组。
从左往右,i,j 之间的元素选择最低的高度,width = j-i+1。
面积 area = (j-i+1) * min(i ... j);
解法
/**
* 最大的长方形面积
*
* 1. 首先直接暴力计算一遍
*
*
* @param heights 高度数组
* @return 结果
*/
public int largestRectangleArea(int[] heights) {
// 最大值
int max = Integer.MIN_VALUE;
for(int i = 0; i < heights.length; i++) {
for(int j = i; j < heights.length; j++) {
// 对比
int width = j - i + 1;
// 应该是从 i..j的最小值
int minHeight = min(heights, i, j);
max = Math.max(width * minHeight, max);
}
}
return max;
}
private int min(int[] nums,
int i,
int j) {
int min = Integer.MAX_VALUE;
for(int k = i; k <= j; k++) {
min = Math.min(min, nums[k]);
}
return min;
}
当然,这种解法会在 87 / 98 TEL。
V2-改进算法
思路
For any bar i the maximum rectangle is of width r - l - 1 where r - is the last coordinate of the bar to the right with height h[r] >= h[i] and l - is the last coordinate of the bar to the left which height h[l] >= h[i]
So if for any i coordinate we know his utmost higher (or of the same height) neighbors to the right and to the left, we can easily find the largest rectangle:
对于任何条 i,最大矩形的宽度为 r - l - 1,其中 r - 是条右侧的最后一个坐标,高度为 h[r] >= h[i],l - 是条的最后一个坐标 向左高度 h[l] >= h[i]
因此,如果对于任何 i 坐标,我们知道他在右侧和左侧的最高(或相同高度)邻居,我们可以轻松找到最大的矩形:
int maxArea = 0;
for (int i = 0; i < height.length; i++) {
maxArea = Math.max(maxArea, height[i] * (lessFromRight[i] - lessFromLeft[i] - 1));
}
The main trick is how to effectively calculate lessFromRight and lessFromLeft arrays.
The trivial solution is to use O(n^2) solution and for each i element first find his left/right heighbour in the second inner loop just iterating back or forward:
主要技巧是如何有效地计算 lessFromRight 和 lessFromLeft 数组。
简单的解决方案是使用 O(n^2) 解决方案,对于每个 i 元素,首先在第二个内部循环中找到他的左/右 heighbour 只是向后或向前迭代:
for (int i = 1; i < height.length; i++) {
int p = i - 1;
while (p >= 0 && height[p] >= height[i]) {
p--;
}
lessFromLeft[i] = p;
}
The only line change shifts this algorithm from O(n^2) to O(n) complexity: we don't need to rescan each item to the left - we can reuse results of previous calculations and "jump" through indices in quick manner:
唯一的行变化将该算法从 O(n^2) 复杂度转变为 O(n) 复杂度:我们不需要向左重新扫描每个项目 - 我们可以重用先前计算的结果并快速“跳转”索引 :
while (p >= 0 && height[p] >= height[i]) {
p = lessFromLeft[p];
}
一点额外的解释
r l
The meaning of r and l is somewhat confusing, to put them more accurately:
l: the first coordinate of the bar to the left with height h[l] < h[i].
r: the first coordinate of the bar to the right with height h[r] < h[i].
p = lessFromLeft[p]
Here's the intuition to understand p = lessFromLeft[p]; :
Consider the test case
indices.......... : 0 1 2 3 4 5 6 7 8 9 10 11
heights.......... : 4 9 8 7 6 5 9 8 7 6 5 4.
lessFromLeft :-1 0 0 0 0 0 5 5 5 5 . .
In this, when we reach 5 at index 10, we start searching for idx=9, i.e. p points at 6.
6 > 5.
Now, we want something which is smaller than 5, so it should definitely be smaller than 6. So 6 says to 5:
I've already done the effort to find the nearest number that's smaller than me and you needn't traverse the array again till that point. My lessFromLeft points at index 5 and all the elements between that and me are greater than me so they are surely greater than you. So just jump to that index and start searching from there.
So you next p directly points at idx = 5, at value 5.
There, this 5 again says the same statement to current 5 and asks it to jump directly to idx = 0. So in the second iteration itself, our search has reached idx=0 and that's our answer for the current element.
Similarly, for the next element 4, it'll take 3 steps.
And for all the elements following 4, if they are greater than 4, their search will stop at 4 itself.
Bottomline: we are not traversing the array again and again. it's O(n).
这是理解 p = lessFromLeft[p]; 的直觉。 :
考虑测试用例
indices.......... : 0 1 2 3 4 5 6 7 8 9 10 11
heights.......... : 4 9 8 7 6 5 9 8 7 6 5 4.
lessFromLeft :-1 0 0 0 0 0 5 5 5 5 . .
在这种情况下,当我们在索引 10 处达到 5 时,我们开始搜索 idx=9,即 p 指向 6。
6 > 5。
现在,我们想要小于 5 的值,所以它肯定小于 6。所以 6 对 5 说:
我已经努力找到比我小的最接近的数字,到那时你不需要再次遍历数组。
我的 lessFromLeft 指向索引 5,它和我之间的所有元素都比我大,所以它们肯定比你大。 所以只需跳转到该索引并从那里开始搜索。
所以你接下来 p 直接指向 idx = 5,值为 5。
在那里,这个 5 再次对当前 5 说同样的语句,并要求它直接跳转到 idx = 0。所以在第二次迭代中,我们的搜索已经到达 idx=0,这就是我们对当前元素的答案。
同样,对于下一个元素 4,它需要 3 个步骤。
而对于 4 之后的所有元素,如果它们都大于 4,则它们的搜索将停止在 4 本身。
底线:我们不是一次又一次地遍历数组。 它是 O(n)。
完整实现
public static int largestRectangleArea(int[] height) {
if (height == null || height.length == 0) {
return 0;
}
int[] lessFromLeft = new int[height.length]; // idx of the first bar the left that is lower than current
int[] lessFromRight = new int[height.length]; // idx of the first bar the right that is lower than current
lessFromRight[height.length - 1] = height.length;
lessFromLeft[0] = -1;
for (int i = 1; i < height.length; i++) {
int p = i - 1;
while (p >= 0 && height[p] >= height[i]) {
p = lessFromLeft[p];
}
lessFromLeft[i] = p;
}
for (int i = height.length - 2; i >= 0; i--) {
int p = i + 1;
while (p < height.length && height[p] >= height[i]) {
p = lessFromRight[p];
}
lessFromRight[i] = p;
}
int maxArea = 0;
for (int i = 0; i < height.length; i++) {
maxArea = Math.max(maxArea, height[i] * (lessFromRight[i] - lessFromLeft[i] - 1));
}
return maxArea;
}
这个解法确实非常震撼。
(1)一个是对于最大矩形的理解
(2)O(N) 算出 lessFromRight/lessFromLeft
参考资料
https://leetcode.com/problems/largest-rectangle-in-histogram/solutions/28902/5ms-o-n-java-solution-explained-beats-96/?orderBy=most_votes
