204. Count Primes
给定一个整数 n,返回严格小于 n 的素数的个数。
Ex
Example 1:
Input: n = 10
Output: 4
Explanation: There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
Example 2:
Input: n = 0
Output: 0
Example 3:
Input: n = 1
Output: 0
Constraints:
0 <= n <= 5 * 10^6
V1-基本算法 Sieve of Eratosthenes
算法
对于算法的介绍,统一参考下面的。
核心思路:
1) 0, 1 不是素数
2)从 2…n, 把素数作为标准,然后把这个素数的倍数全部置为 false。
实现
public int countPrimes(int n) {
if(n <= 2) {
return 0;
}
boolean[] isPrimes = new boolean[n+1];
Arrays.fill(isPrimes, true);
isPrimes[0] = false;
isPrimes[1] = false;
for(int i = 2; i <= n; i++) {
if(isPrimes[i] && (long)i * i <= n) {
// 把一个基本数的倍数,全部置为 false
for (int j = i * i; j <= n; j += i) {
isPrimes[j] = false;
}
}
}
// 计算总数
int count = 0;
for(int i = 0; i < isPrimes.length; i++) {
if(isPrimes[i] && i < n) {
count++;
}
}
return count;
}
耗时 180ms, 优于 35.11%。
V2-只到根
显然,找到所有素数直到 n,仅通过不超过根的素数进行筛选就足够了 n。
class Solution {
public int countPrimes(int n) {
if(n <= 2) {
return 0;
}
boolean[] isPrimes = new boolean[n+1];
Arrays.fill(isPrimes, true);
isPrimes[0] = false;
isPrimes[1] = false;
for(int i = 2; i*i <= n; i++) {
if(isPrimes[i]) {
// 把一个基本数的倍数,全部置为 false
for (int j = i * i; j <= n; j += i) {
isPrimes[j] = false;
}
}
}
// 计算总数
int count = 0;
for(int i = 0; i < isPrimes.length; i++) {
if(isPrimes[i] && i < n) {
count++;
}
}
return count;
}
}
Runtime 121 ms Beats 80.16%
V3-只看奇数
思路:偶数为,都是 2 的倍数,其实不需要看。
public int countPrimes(int n) {
if(n <= 2) {
return 0;
}
boolean[] isPrimes = new boolean[n+1];
for(int i = 0; i < n; i++) {
if(i % 2 != 0) {
// 偶数位全为false
isPrimes[i] = true;
}
}
// 2 是特例
isPrimes[2] = true;
for(int i = 2; i*i <= n; i++) {
if(isPrimes[i]) {
// 把一个基本数的倍数,全部置为 false
for (int j = i * i; j <= n; j += i) {
isPrimes[j] = false;
}
}
}
// 计算总数
int count = 0;
for(int i = 0; i < isPrimes.length; i++) {
if(isPrimes[i] && i < n) {
count++;
}
}
return count;
}
PS: 实际效果看起来一般。
V4-线性算法
实现如下:
class Solution {
public int countPrimes(int n) {
int count = 0;
int[] lp = new int[n+1];
List<Integer> pr = new ArrayList<>(n);
for(int i = 2; i <= n; i++) {
if(lp[i] == 0) {
lp[i] = i;
pr.add(i);
// 严格小于
if(i < n) {
count++;
}
}
for (int j = 0; i * pr.get(j) <= n; ++j) {
lp[i * pr.get(j)] = pr.get(j);
if (pr.get(j) == lp[i]) {
break;
}
}
}
return count;
}
}
Runtime 378 ms Beats 8.67%
效果反而不是很好。
可见实际的复杂度,在实际中未必是最好的。
Sieve of Eratosthenes
Sieve of Eratosthenes 是一种用于查找线段中所有素数的算法,[1:n], 使用 O(n*loglogn) 的操作。
算法
算法很简单:
-
一开始我们写下 2 到 n。
-
我们将所有 2 的真倍数(因为 2 是最小的素数)标记为合数。
-
一个数的适当倍数 x ,是一个大于 x 可被整除 x。 然后我们找到下一个没有被标记为合数的数字,在本例中它是 3。
这意味着 3 是质数,我们将 3 的所有适当倍数标记为合数。
下一个未标记的数字是 5,它是下一个素数,我们标记它的所有真倍数。
我们继续这个过程,直到我们处理了行中的所有数字。
在下图中,您可以看到用于计算范围内所有素数的算法的可视化 [1; 16]。
可以看出,我们经常多次将数字标记为合数。
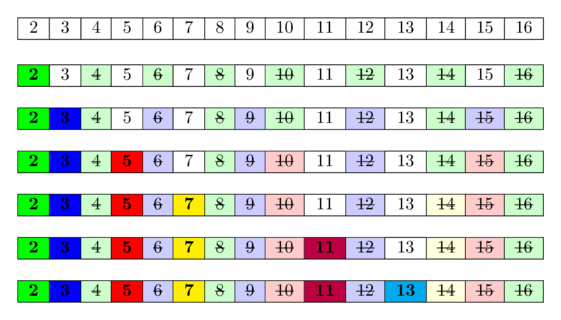
背后的想法是:如果没有较小的素数能整除一个数,则该数是素数。 由于我们按顺序遍历素数,因此我们已经将所有可被至少一个素数整除的数字标记为可整除。 因此,如果我们到达一个单元格并且它没有被标记,那么它不能被任何更小的素数整除,因此必须是素数。
实现
int n;
vector<bool> is_prime(n+1, true);
is_prime[0] = is_prime[1] = false;
for (int i = 2; i <= n; i++) {
// 基本的数学,作为倍数的
if (is_prime[i] && (long long)i * i <= n) {
// 把一个基本数的倍数,全部置为 false
for (int j = i * i; j <= n; j += i)
is_prime[j] = false;
}
}
此代码首先将除零和一之外的所有数字标记为潜在素数,然后开始筛选合数的过程。
为此,它遍历所有数字 2 至 n。
如果当前数 i 是质数,它标记所有是以下数的倍数的数 i 作为合数,从 i^2。 这已经是对实现它的天真的方式的优化,并且允许所有较小的数字是 i 必然还有一个质因数小于 i,所以他们都已经过筛了。
自从 i^2 很容易溢出 int 类型,额外的验证是在第二个嵌套循环之前使用 long long 类型完成的。
使用这样的实现算法消耗 O(n) 内存(显然)并执行 O(nloglog n)。
Eratosthenes 筛法的不同优化
该算法的最大弱点是,它多次“遍历”内存,只操作单个元素。
这对缓存不是很友好。
正因为如此,隐藏在 O(nloglog n) 比较大。
此外,消耗的内存是大的瓶颈 n。
下面介绍的方法使我们能够减少执行操作的数量,并显着缩短消耗的内存。
筛选到根 (Sieving till root)
显然,找到所有素数直到 n,仅通过不超过根的素数进行筛选就足够了 n。
int n;
vector<bool> is_prime(n+1, true);
is_prime[0] = is_prime[1] = false;
for (int i = 2; i * i <= n; i++) {
if (is_prime[i]) {
for (int j = i * i; j <= n; j += i)
is_prime[j] = false;
}
}
这种优化不会影响复杂性(实际上,通过重复上面给出的证明,我们将得到评估 nlnln Sqrt(n) + O(n),根据对数的性质渐近相同),虽然运算次数会明显减少。
仅按奇数筛选 (Sieving by the odd numbers only)
因为所有偶数(除了 2 ) 是复合的,我们可以完全停止检查偶数。
相反,我们只需要对奇数进行操作。
首先,它将允许我们将所需内存减半。
其次,它将算法执行的操作数量减少大约一半。
内存消耗和操作速度 (Memory consumption and speed of operations)
我们应该注意到,Eratosthenes 筛法的这两个实现使用 n 位内存,使用数据结构 vector<bool>。
vector<bool> 不是存储一系列 bool 的常规容器(因为在大多数计算机体系结构中,bool 占用一个字节的内存)。
它是 vector<T> 的内存优化特化,只消耗 n / 8。
现代处理器架构处理字节比处理位更有效,因为它们通常不能直接访问位。
因此,在 vector<bool> 之下,将位存储在一个大的连续内存中,以几个字节的块访问内存,并使用位掩码和位移等位操作提取/设置位。
因此,当您使用 vector<bool> 读取或写入位时会产生一定的开销,并且通常使用 vector<char>(每个条目使用 1 个字节,因此内存量增加 8 倍)速度更快。
但是,对于使用 vector<bool> 的 Eratosthenes 筛法的简单实现,速度更快。
您受到将数据加载到缓存中的速度的限制,因此使用较少的内存会带来很大的优势。
基准测试(链接)显示,使用 vector<bool> 比使用 vector<char> 快 1.4 到 1.7 倍。
同样的考虑也适用于 bitset。 它也是一种存储位的有效方式,类似于 vector<bool>,所以它只需要 n / 8 字节的内存,但访问元素的速度有点慢。
在上面的基准测试中,bitset 的表现比 vector<bool> 差一点。 bitset 的另一个缺点是您需要在编译时知道大小。
分段筛 (Segmented Sieve)
从优化“筛选到根”可以看出,不需要始终保留整个数组 is_prime[1…n]。
对于筛分,只保留质数直到根 n,即素数[1…sqrt(n)],将完整的范围分割成块,分别对每个块进行筛选。
让 s 是决定块大小的常数,那么我们有 ceil(n/s) 完全块,块 k(k=0...floor(n/s)) 包含段中的数字 [ks; ks + s - 1]。
我们可以轮流处理块,即对于每个块 k 我们将遍历所有素数(从 1 至 sqrt(n) ) 并使用它们进行筛分。
值得注意的是,我们在处理第一个数字时必须稍微修改策略:
首先,所有素数来自 [1; sqrt(n)] 不应该删除自己; 第二,数字 0 和 1 应标记为非素数。
在处理最后一个块时,不应忘记最后需要的数字 n 不必位于块的末尾。
如前所述,Eratosthenes 筛法的典型实现受限于将数据加载到 CPU 缓存中的速度。
通过分割潜在素数的范围 [1; n] 分成更小的块,我们永远不必同时在内存中保留多个块,并且所有操作都更加缓存友好。
由于我们现在不再受缓存速度的限制,我们可以将 vector<bool> 替换为 vector<char>,并获得一些额外的性能,因为处理器可以直接处理字节读写,而不需要依赖 用于提取单个位的位操作。
基准测试(链接)显示,在这种情况下使用 vector<char> 比使用 vector<bool> 快大约 3 倍。
提醒一句:这些数字可能因体系结构、编译器和优化级别而异。
这里我们有一个计算小于或等于素数的实现 n 使用块筛分法。
int count_primes(int n) {
const int S = 10000;
vector<int> primes;
int nsqrt = sqrt(n);
vector<char> is_prime(nsqrt + 2, true);
for (int i = 2; i <= nsqrt; i++) {
if (is_prime[i]) {
primes.push_back(i);
for (int j = i * i; j <= nsqrt; j += i)
is_prime[j] = false;
}
}
int result = 0;
vector<char> block(S);
for (int k = 0; k * S <= n; k++) {
fill(block.begin(), block.end(), true);
int start = k * S;
for (int p : primes) {
int start_idx = (start + p - 1) / p;
int j = max(start_idx, p) * p - start;
for (; j < S; j += p)
block[j] = false;
}
if (k == 0)
block[0] = block[1] = false;
for (int i = 0; i < S && start + i <= n; i++) {
if (block[i])
result++;
}
}
return result;
}
块筛的运行时间与常规埃拉托色尼筛相同(除非块的尺寸非常小),但所需内存将缩短为 O(sqrt(n) + S) 并且我们有更好的缓存结果。
另一方面,对于每对来自 [1; sqrt(n)],对于较小的块大小,情况会更糟。
因此,在选择常数时有必要保持平衡 S。
我们在块大小介于 10^4 和 10^5。
查找范围内的素数
有时我们需要找到一个范围内的所有质数 [L,R] 小尺寸(例如 R - L + 1 约等于 1e7 ), 其中 R 可以非常大(例如 1e12).
为了解决这样的问题,我们可以使用分段筛的思想。
我们预先生成所有质数直到 sqrt(R) ,并用这些素数来标记线段中的所有合数 [L, R]。
vector<char> segmentedSieve(long long L, long long R) {
// generate all primes up to sqrt(R)
long long lim = sqrt(R);
vector<char> mark(lim + 1, false);
vector<long long> primes;
for (long long i = 2; i <= lim; ++i) {
if (!mark[i]) {
primes.emplace_back(i);
for (long long j = i * i; j <= lim; j += i)
mark[j] = true;
}
}
vector<char> isPrime(R - L + 1, true);
for (long long i : primes)
for (long long j = max(i * i, (L + i - 1) / i * i); j <= R; j += i)
isPrime[j - L] = false;
if (L == 1)
isPrime[0] = false;
return isPrime;
}
这种方法的时间复杂度是 O( (R-L+1) loglog(R) + sqrt(R)loglog * sqrt(R))
我们也有可能不预先生成所有素数:
vector<char> segmentedSieveNoPreGen(long long L, long long R) {
vector<char> isPrime(R - L + 1, true);
long long lim = sqrt(R);
for (long long i = 2; i <= lim; ++i)
for (long long j = max(i * i, (L + i - 1) / i * i); j <= R; j += i)
isPrime[j - L] = false;
if (L == 1)
isPrime[0] = false;
return isPrime;
}
显然,这个复杂度 O( (R-L+1) log(R) + sqrt(R) 更加糟糕,但是实践中也许运行的更快。
线性时间修改
我们可以修改算法,使其仅具有线性时间复杂度。
这种方法在文章 Linear Sieve 中有所描述。
但是,该算法也有其自身的弱点。
Linear Sieve
给定一个数字 n , 找出一个段中的所有素数 [2;n]。
解决任务的标准方法是使用埃拉托色尼筛法。
这个算法很简单,但是有runtime O(nloglogn)。
虽然有很多已知的算法具有次线性运行时间(即 o(n)),下面描述的算法因其简单而有趣:它并不比埃拉托色尼的经典筛法复杂。
此外,此处给出的算法计算段中所有数字的因式分解 [2; n] 作为副作用,这在许多实际应用中很有帮助。
给定算法的弱点在于使用比 Eratosthenes 的经典筛法更多的内存:
它需要一个数组 n 个数,而对于埃拉托色尼的经典筛法来说,有 n 内存位(减少 32 倍)。
因此,仅在订单数量之前使用所描述的算法是有意义的 10^7 并且不会更高。
该算法归功于 Paul Pritchard。 它是算法 3.3 的一个变体(Pritchard,1987:参见文末的参考资料)。
算法
我们的目标是计算最小质因数 lp[i] 代表每个数字 i 在细分市场中 [2; n]。
此外,我们需要存储所有找到的素数的列表——我们称它为 pr[]。
我们将初始化值 lp[i] 带零,这意味着我们假设所有数字都是质数。
在算法执行期间,该数组将逐渐填充。
现在我们将遍历从 2 到 n。
目前的 lp[i] 有两种情况:
1) lp[i] == 0, 那意味着 i 是素数,即我们还没有找到任何更小的因子。 因此,我们分配 lp [i] = i 并添加 i 到列表 pr[] 末尾。
2) lp[i] != 0,那意味着 i 是合数,它的最小质因数是 lp[i]。
在这两种情况下,我们更新的值 lp[] 可被整除的数 i。
但是,我们的目标是学会这样做以设定一个值 lp[] 每个数字最多一次。
我们可以这样做:
让我们考虑数字 x_j = i * p_j ,其中 p_j 都是小于或等于的素数 lp[i] (这就是为什么我们需要存储所有素数的列表)。
我们将设置一个新值 lp[x_j] = p_j 对于这种形式的所有数字。
该算法及其运行时的正确性证明可以在实现后找到。
实现
c语言
const int N = 10000000;
vector<int> lp(N+1);
vector<int> pr;
for (int i=2; i <= N; ++i) {
if (lp[i] == 0) {
lp[i] = i;
pr.push_back(i);
}
for (int j = 0; i * pr[j] <= N; ++j) {
lp[i * pr[j]] = pr[j];
if (pr[j] == lp[i]) {
break;
}
}
}
Runtime & Memory
时间复杂度:O(n),但是运行效果其实和经典算法 O(nloglogn) 差别不大。
参考资料
https://leetcode.com/problems/count-primes/description/
http://warp.povusers.org/programming/sieve_of_eratosthenes.html
https://cp-algorithms.com/algebra/prime-sieve-linear.html
