208 实现 Trie (前缀树)
Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
示例:
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True
```
## 提示:
1 <= word.length, prefix.length <= 2000
word 和 prefix 仅由小写英文字母组成
insert、search 和 startsWith 调用次数 总计 不超过 3 * 10^4 次
# 介绍 Trie🌳
Trie 是一颗非典型的多叉树模型,多叉好理解,即每个结点的分支数量可能为多个。
为什么说非典型呢?
因为它和一般的多叉树不一样,尤其在结点的数据结构设计上,比如一般的多叉树的结点是这样的:
```c
struct TreeNode {
VALUETYPE value; //结点值
TreeNode* children[NUM]; //指向孩子结点
};
而 Trie 的结点是这样的(假设只包含’a’~’z’中的字符):
struct TrieNode {
bool isEnd; //该结点是否是一个串的结束
TrieNode* next[26]; //字母映射表
};
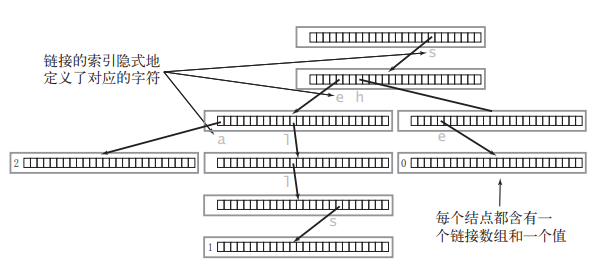
要想学会 Trie 就得先明白它的结点设计。我们可以看到TrieNode结点中并没有直接保存字符值的数据成员,那它是怎么保存字符的呢?
这时字母映射表next 的妙用就体现了,TrieNode* next[26] 中保存了对当前结点而言下一个可能出现的所有字符的链接,因此我们可以通过一个父结点来预知它所有子结点的值:
for (int i = 0; i < 26; i++) {
char ch = 'a' + i;
if (parentNode->next[i] == NULL) {
说明父结点的后一个字母不可为 ch
} else {
说明父结点的后一个字母可以是 ch
}
}
我们来看个例子吧。
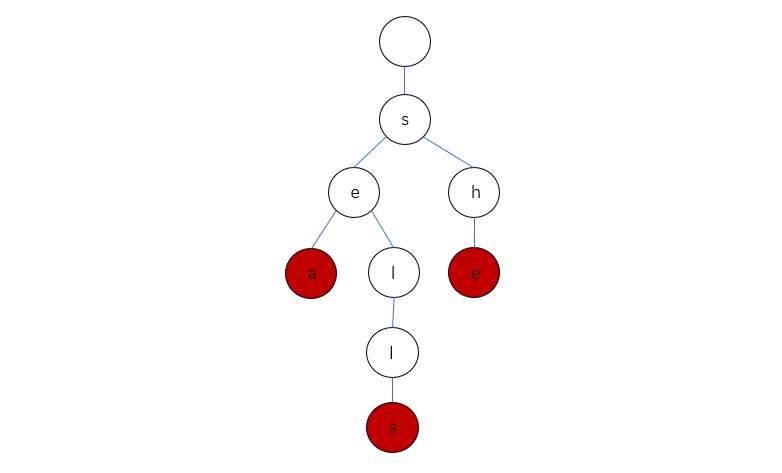
想象以下,包含三个单词 “sea”,”sells”,”she” 的 Trie 会长啥样呢?
它的真实情况是这样的:
Trie 中一般都含有大量的空链接,因此在绘制一棵单词查找树时一般会忽略空链接,同时为了方便理解我们可以画成这样:
接下来我们一起来实现对 Trie 的一些常用操作方法。
常规操作
定义
class Trie {
private:
bool isEnd;
Trie* next[26];
public:
//方法将在下文实现...
};
插入
描述:向 Trie 中插入一个单词 word
实现:这个操作和构建链表很像。首先从根结点的子结点开始与 word 第一个字符进行匹配,一直匹配到前缀链上没有对应的字符,这时开始不断开辟新的结点,直到插入完 word 的最后一个字符,同时还要将最后一个结点isEnd = true;,表示它是一个单词的末尾。
void insert(string word) {
Trie* node = this;
for (char c : word) {
if (node->next[c-'a'] == NULL) {
node->next[c-'a'] = new Trie();
}
node = node->next[c-'a'];
}
node->isEnd = true;
}
查找
描述:查找 Trie 中是否存在单词 word
实现:从根结点的子结点开始,一直向下匹配即可,如果出现结点值为空就返回 false,如果匹配到了最后一个字符,那我们只需判断 node->isEnd即可。
bool search(string word) {
Trie* node = this;
for (char c : word) {
node = node->next[c - 'a'];
if (node == NULL) {
return false;
}
}
return node->isEnd;
}
前缀匹配
描述:判断 Trie 中是或有以 prefix 为前缀的单词
实现:和 search 操作类似,只是不需要判断最后一个字符结点的isEnd,因为既然能匹配到最后一个字符,那后面一定有单词是以它为前缀的。
bool startsWith(string prefix) {
Trie* node = this;
for (char c : prefix) {
node = node->next[c-'a'];
if (node == NULL) {
return false;
}
}
return true;
}
到这我们就已经实现了对 Trie 的一些基本操作,这样我们对 Trie 就有了进一步的理解。完整代码我贴在了文末。
总结
通过以上介绍和代码实现我们可以总结出 Trie 的几点性质:
Trie 的形状和单词的插入或删除顺序无关,也就是说对于任意给定的一组单词,Trie 的形状都是唯一的。
查找或插入一个长度为 L 的单词,访问 next 数组的次数最多为 L+1,和 Trie 中包含多少个单词无关。
Trie 的每个结点中都保留着一个字母表,这是很耗费空间的。
如果 Trie 的高度为 n,字母表的大小为 m,最坏的情况是 Trie 中还不存在前缀相同的单词,那空间复杂度就为 O(m^n)
最后,关于 Trie 的应用场景,希望你能记住 8 个字:一次建树,多次查询。
java 实现
class Trie {
private class TrieNode {
private boolean isEnd;
private TrieNode[] next;
public TrieNode() {
this.isEnd = false;
next = new TrieNode[26];
}
}
// 根节点
private TrieNode root;
public Trie() {
// 初始化
root = new TrieNode();
}
public void insert(String word) {
TrieNode cur = root;
for(int i = 0; i < word.length(); i++) {
int ci = word.charAt(i) - 'a';
if(cur.next[ci] == null) {
cur.next[ci] = new TrieNode();
}
cur = cur.next[ci];
}
// 单词结束
cur.isEnd = true;
}
public boolean search(String word) {
TrieNode cur = root;
for(int i = 0; i < word.length(); i++) {
int ci = word.charAt(i) - 'a';
if(cur.next[ci] == null) {
return false;
}
cur = cur.next[ci];
}
// 单词结束
return cur.isEnd;
}
public boolean startsWith(String prefix) {
TrieNode cur = root;
for(int i = 0; i < prefix.length(); i++) {
int ci = prefix.charAt(i) - 'a';
if(cur.next[ci] == null) {
return false;
}
cur = cur.next[ci];
}
// 单词结束
return true;
}
}
211. 添加与搜索单词 - 数据结构设计
请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。
实现词典类 WordDictionary :
WordDictionary() 初始化词典对象
void addWord(word) 将 word 添加到数据结构中,之后可以对它进行匹配
bool search(word) 如果数据结构中存在字符串与 word 匹配,则返回 true ;否则,返回 false 。word 中可能包含一些 ‘.’ ,每个 . 都可以表示任何一个字母。
示例:
输入:
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
输出:
[null,null,null,null,false,true,true,true]
解释:
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // 返回 False
wordDictionary.search("bad"); // 返回 True
wordDictionary.search(".ad"); // 返回 True
wordDictionary.search("b.."); // 返回 True
提示:
1 <= word.length <= 25
addWord 中的 word 由小写英文字母组成
search 中的 word 由 ‘.’ 或小写英文字母组成
最多调用 10^4 次 addWord 和 search
V1-基于 Trie Tree
思路
整体的单词查询,和上面的实现没有太大差别,但是有一个 . 的特殊场景。
java 实现
节点定义和单词增加,都是不变的。
search 通过回溯的方式,找到所有可能匹配的场景。
class WordDictionary {
private class TrieNode {
private boolean isEnd;
private TrieNode[] next;
public TrieNode() {
this.isEnd = false;
next = new TrieNode[26];
}
}
// 根节点
private TrieNode root;
public WordDictionary() {
root = new TrieNode();
}
// 添加
public void addWord(String word) {
TrieNode cur = root;
for(int i = 0; i < word.length(); i++) {
int ci = word.charAt(i) - 'a';
if(cur.next[ci] == null) {
cur.next[ci] = new TrieNode();
}
cur = cur.next[ci];
}
// 单词结束
cur.isEnd = true;
}
// word . 可以匹配任意字符
public boolean search(String word) {
return match(word.toCharArray(), 0, root);
}
private boolean match(char[] chs, int k, TrieNode node) {
// 终止条件
if (k == chs.length) {
return node.isEnd;
}
if (chs[k] == '.') {
// 任意匹配
for (int i = 0; i < node.next.length; i++) {
if (node.next[i] != null && match(chs, k + 1, node.next[i])) {
return true;
}
}
} else {
// 精准匹配
return node.next[chs[k] - 'a'] != null && match(chs, k + 1, node.next[chs[k] - 'a']);
}
return false;
}
}
212. 单词搜索 II
给定一个 m x n 二维字符网格 board 和一个单词(字符串)列表 words, 返回所有二维网格上的单词 。
单词必须按照字母顺序,通过 相邻的单元格 内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。
同一个单元格内的字母在一个单词中不允许被重复使用。
例子
示例 1:

输入:board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
输出:["eat","oath"]
示例 2:
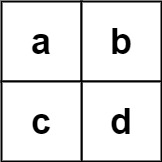
输入:board = [["a","b"],["c","d"]], words = ["abcb"]
输出:[]
```
## 提示:
m == board.length
n == board[i].length
1 <= m, n <= 12
board[i][j] 是一个小写英文字母
1 <= words.length <= 3 * 10^4
1 <= words[i].length <= 10
words[i] 由小写英文字母组成
words 中的所有字符串互不相同
## V1-循环处理
我们可以直接复用 [79. Word Search](https://leetcode.com/problems/word-search/)
### 思路
直接复用 079 的算法。
### java 实现
```java
/**
* 这一题,使用原来的解法,问题并不大。079
*
* @param board
* @param words
* @return
*/
public List<String> findWords(char[][] board, String[] words) {
List<String> resultList = new ArrayList<>();
for(String word : words) {
if(exist(board, word)) {
resultList.add(word);
}
}
return resultList;
}
public boolean exist(char[][] board, String word) {
// 统一转换,可以避免 charAt 的越界校验
char[] chars = word.toCharArray();
int m = board.length;
int n = board[0].length;
boolean[][] visited = new boolean[m][n];
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
if(search(board, chars, visited, i, j, 0)) {
return true;
}
}
}
return false;
}
// 实际上核心思想还是回溯
// index 从零开始
private boolean search(char[][] board, char[] chars,
boolean[][] visited,
int i, int j, int index) {
// 终止条件
if(index == chars.length) {
return true;
}
if(i >= board.length || i < 0
|| j >= board[i].length || j < 0
|| board[i][j] != chars[index]
|| visited[i][j]){
return false;
}
visited[i][j] = true;
// 上下左右
if(search(board, chars, visited, i-1, j, index+1) ||
search(board, chars, visited,i+1, j, index+1) ||
search(board, chars, visited, i, j-1, index+1) ||
search(board, chars, visited, i, j+1, index+1)){
return true;
}
// 回溯
visited[i][j] = false;
return false;
}
评价
这个算法会在 62/64 的用例超时。
原因也比较简单,我们每一个单词都是从头开始处理,每次遍历没有复用任何信息。
能不能把单词的处理,复用起来呢?
V2-通过 Trie Tree
思路
我们引入 Trie Tree,把单词构建成一个前缀树。
然后处理这棵前缀树,可以达到复用的效果。
java 实现
有两个部分组成:
1)trie-tree 构建,参见 T208 实现。
2)dfs 判断是否匹配
这里如果匹配,将其放在结果中。
import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.util.Set;
/**
* @author binbin.hou
* @since 1.0.0
*/
public class T212_WordSearchV2 {
/**
* 优化思路:
*
* 1. 可以结合 trie 优化性能。
*
* 2. trie-tree 的实现参见 T208
*
* @param board
* @param words
* @return
*/
private Set<String> res = new HashSet<String>();
public List<String> findWords(char[][] board, String[] words) {
// 构建 trie
TrieTree trieTree = new TrieTree();
for(String word : words) {
trieTree.insert(word);
}
//dfs 处理
int m = board.length;
int n = board[0].length;
boolean[][] visited = new boolean[m][n];
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
dfs(board, visited, trieTree, i, j, "");
}
}
return new ArrayList<>(res);
}
// 实际上核心思想还是回溯
// index 从零开始
private void dfs(char[][] board,
boolean[][] visited,
TrieTree trieTree,
int i,
int j,
String str) {
// 终止条件
if(i >= board.length
|| i < 0
|| j >= board[i].length
|| j < 0
|| visited[i][j]){
return;
}
str += board[i][j];
// 剪枝,没有匹配的前缀
if(!trieTree.startsWith(str)) {
return;
}
// 满足条件的结果
if(trieTree.search(str)) {
res.add(str);
}
visited[i][j] = true;
// 上下左右
dfs(board, visited, trieTree, i - 1, j, str);
dfs(board, visited, trieTree, i + 1, j, str);
dfs(board, visited, trieTree, i, j - 1, str);
dfs(board, visited, trieTree, i, j + 1, str);
// 回溯
visited[i][j] = false;
}
/**
* 前缀树实现 T208
*/
private class TrieTree {
private class TrieNode {
private boolean isEnd;
private TrieNode[] next;
public TrieNode() {
this.isEnd = false;
next = new TrieNode[26];
}
}
// 根节点
private TrieNode root;
public TrieTree() {
// 初始化
root = new TrieNode();
}
public void insert(String word) {
TrieNode cur = root;
for(int i = 0; i < word.length(); i++) {
int ci = word.charAt(i) - 'a';
if(cur.next[ci] == null) {
cur.next[ci] = new TrieNode();
}
cur = cur.next[ci];
}
// 单词结束
cur.isEnd = true;
}
public boolean search(String word) {
TrieNode cur = root;
for(int i = 0; i < word.length(); i++) {
int ci = word.charAt(i) - 'a';
if(cur.next[ci] == null) {
return false;
}
cur = cur.next[ci];
}
// 单词结束
return cur.isEnd;
}
public boolean startsWith(String prefix) {
TrieNode cur = root;
for(int i = 0; i < prefix.length(); i++) {
int ci = prefix.charAt(i) - 'a';
if(cur.next[ci] == null) {
return false;
}
cur = cur.next[ci];
}
// 单词结束
return true;
}
}
}
V3-进一步性能优化
思路
如果是我,估计最多止步于 V2 的算法。
不过在学习的时候,还是拜读了 java-15ms-easiest-solution-100-00
这种追求卓越的思想值得敬佩。
请注意:
1. TrieNode 就是我们所需要的。 search 和 startsWith 没用。
2. 无需在 TrieNode 存储字符。 c.next[i] != null 就足够了。
3. 切勿使用 c1 + c2 + c3。 使用字符串生成器。
4. 无需使用 O(n^2) 的额外空间 visited[m][n]。
5. 无需使用 StringBuilder。 将单词本身存储在叶节点就足够了。
6. 无需使用 HashSet 去重。 使用“一次性搜索”trie。
其中共计 6 步的优化策略,值得我们平时使用的时候借鉴。
不过实现会变得更加难懂一些。
java 实现
(1)Trie Tree 简化
只需要构建即可,省略了对应的方法。
因为方法放在 dfs 中实现了。
(2)StringBuilder 替代 string 加法
这个 jdk 优化的也比较好,知道即可。多次拼接,建议使用 StringBuilder。
(3)节省内存
直接通过 board[i][j] = '#'; 替换来节省一个内存空间,可以在类似的题目中使用。
public List<String> findWords(char[][] board, String[] words) {
List<String> res = new ArrayList<>();
TrieNode root = buildTrie(words);
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
dfs (board, i, j, root, res);
}
}
return res;
}
public void dfs(char[][] board, int i, int j, TrieNode p, List<String> res) {
char c = board[i][j];
if (c == '#' || p.next[c - 'a'] == null) {
return;
}
// 通过直接处理,而不是方法。但是这样不利于类的封装。
p = p.next[c - 'a'];
if (p.word != null) { // found one
res.add(p.word);
p.word = null; // de-duplicate
}
// 替换,节省空间
board[i][j] = '#';
if (i > 0) dfs(board, i - 1, j ,p, res);
if (j > 0) dfs(board, i, j - 1, p, res);
if (i < board.length - 1) dfs(board, i + 1, j, p, res);
if (j < board[0].length - 1) dfs(board, i, j + 1, p, res);
board[i][j] = c;
}
public TrieNode buildTrie(String[] words) {
TrieNode root = new TrieNode();
for (String w : words) {
TrieNode p = root;
for (char c : w.toCharArray()) {
int i = c - 'a';
if (p.next[i] == null) p.next[i] = new TrieNode();
p = p.next[i];
}
// 类似于 isEnd
p.word = w;
}
return root;
}
private class TrieNode {
TrieNode[] next = new TrieNode[26];
String word;
}
参考资料
https://leetcode.cn/problems/implement-trie-prefix-tree/
https://leetcode.cn/problems/implement-trie-prefix-tree/solution/trie-tree-de-shi-xian-gua-he-chu-xue-zhe-by-huwt/
https://leetcode.cn/problems/design-add-and-search-words-data-structure/