题目:
城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。
给你所有建筑物的位置和高度,请返回 由这些建筑物形成的 天际线 。
每个建筑物的几何信息由数组 buildings 表示,其中三元组 buildings[i] = [lefti, righti, heighti] 表示:
lefti 是第 i 座建筑物左边缘的 x 坐标。 righti 是第 i 座建筑物右边缘的 x 坐标。 heighti 是第 i 座建筑物的高度。 你可以假设所有的建筑都是完美的长方形,在高度为 0 的绝对平坦的表面上。
天际线 应该表示为由 “关键点” 组成的列表,格式 [[x1,y1],[x2,y2],…] ,并按 x 坐标 进行 排序 。
关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点,y 坐标始终为 0 ,仅用于标记天际线的终点。
此外,任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。
注意:输出天际线中不得有连续的相同高度的水平线。
例如 […[2 3], [4 5], [7 5], [11 5], [12 7]…] 是不正确的答案;三条高度为 5 的线应该在最终输出中合并为一个:[…[2 3], [4 5], [12 7], …]
示例 1:
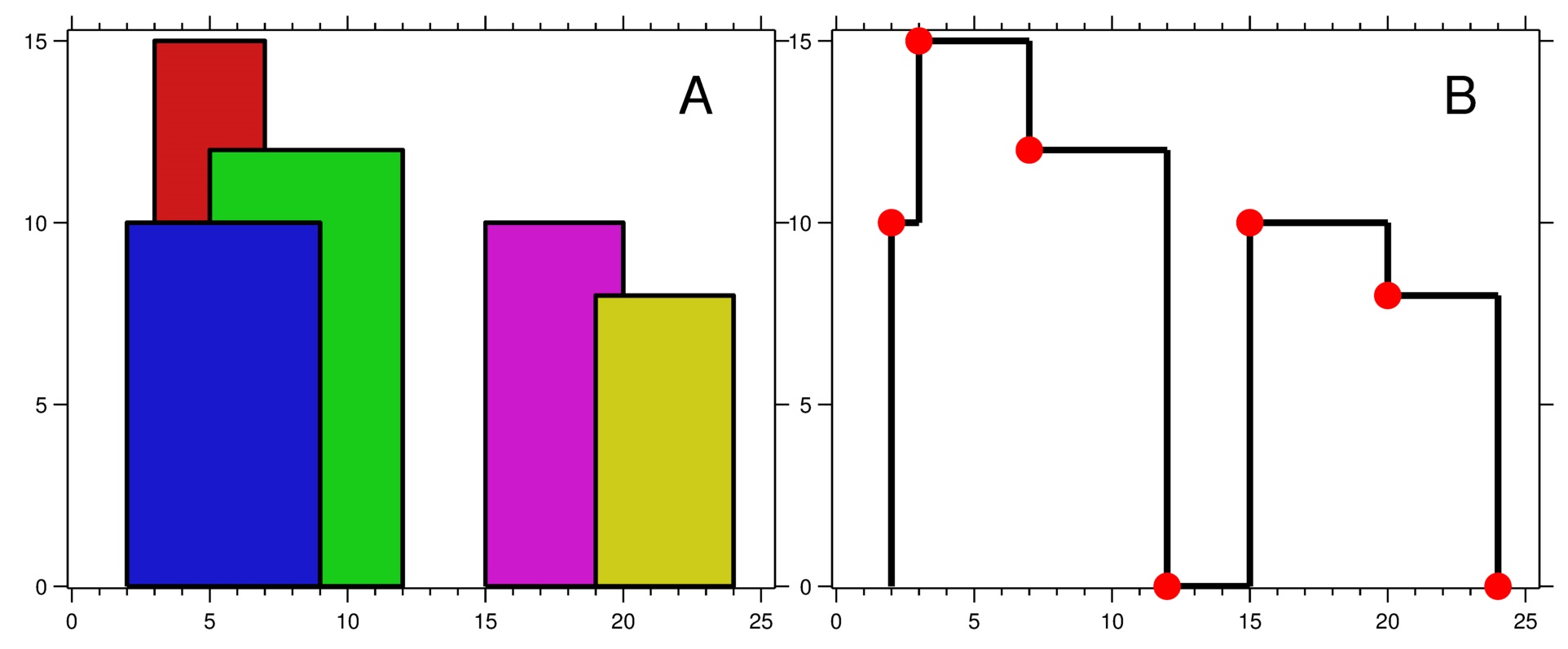
输入:buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]] 输出:[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]] 解释: 图 A 显示输入的所有建筑物的位置和高度, 图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。 示例 2:
输入:buildings = [[0,2,3],[2,5,3]] 输出:[[0,3],[5,0]]
提示:
1 <= buildings.length <= 10^4 0 <= lefti < righti <= 2^31 - 1 1 <= heighti <= 2^31 - 1 buildings 按 lefti 非递减排序
理解
这一套题,非常的抽象。
引用一下别人的解释:
这道题难点在于理解。天际线这一情景十分抽象,我们不如将这道题转化为另一个情景--物种统治问题:
假设[lefti, righti, heighti] 存放的是某一物种的出现、灭绝时间和能力值,某一时刻存活的能力值最高的物种统治世界。要求得每次统治的开始时间和统治物种的能力值。
这样就很容易思考了:
首先用(time,+/-ability)来记录每个物种的出现、灭绝时间(正负号用于区分是出现时间还是灭绝时间),并按照时间顺序排序。
维持一个大顶堆,当一个物种出现时,将对应的能力值丢入大顶堆;当一个物种灭绝时,将对应的能力从大顶堆中拿出。
这样,大顶堆就时刻维持着当前统治的物种的能力值。进而求得每次统治的开始时间和对应能力值。
默认存在一个能力值为0,存在时间无限的憨憨物种兜底。
我们只需要计算一个物种的开始时间+对应的能力值。
解题思路
观察示例不难发现关键点是高度发生变化的第一个点,所以我们可以通过扫描线法来解这个问题。我们首先需要建立一个最小堆,最小堆中维护当前位置最大高度,如果当前的最大高度发生变化就将其加入结果即可。
我们需要关注高度,所以一定会有Hi(从大到小的顺序排序),同时我们希望按照Li的大小(从小到大)排序,所以我们存放的结构就是[Li,-Hi,Ri];还需要考虑最后一个关键点的问题,最后一个关键点高度是0,并且按照Ri从小到大排序,此时我们存放的结构就是[Ri,0,0](将右端点高度看成是0非常关键)。我们将上面的结构进行排序得到一个关键点的集合。
现在思考遍历集合的过程中会出现的问题。
如图所示:

首先,如果高度不是0的话,我们需要将[Hi, Ri](通过Hi确定最大高度,通过Ri确定最大高度的有效位置)加入到最小堆中,以维护当前位置的最大高度。
如果最大高度的右端点已经超过了当前遍历的位置,说明当前最大高度失效,所以将其弹出。
如果高度出现变化,那么我们将变化的高度添加到结果中,此时结果中添加的是[Li,-Hi]。
最后代码非常简洁:
import heapq
class Solution:
def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
points = [(L, -H, R) for L, R, H in buildings] + [(R, 0, 0) for R in set(r for _, r, _ in buildings)]
points.sort()
heap, res = [(0, float('inf'))], [[0, 0]]
for l, nh, r in points:
while heap[0][1] <= l:
heapq.heappop(heap)
if nh:
heapq.heappush(heap, (nh, r))
if res[-1][1] != -heap[0][0]:
res += [[l, -heap[0][0]]]
return res[1:]
这个问题采用分治法也是不错的思路。
需要考虑两个建筑物的合并过程,主要分成三种情况:
left_l < right_l left_l > right_l left_l = right_l
其中left_l表示左边建筑物的l坐标,right_l表示右边建筑物的l坐标。
第一种情况如图所示:

其中lh和rh用于记录左右建筑物的高度,初始值为0。
此时需要添加的点的坐标就是[left_l, max(left_h, rh)],其中left_h表示当前左边建筑物的高度。
第二种情况如图所示:

此时需要添加的点的坐标就是[right_l, max(right_h, lh)],其中right_h表示当前右边建筑物的高度。
第三种情况如图所示:

此时需要添加的点的坐标就是[left_l, max(right_h, left_h)]。
最后需要思考边界问题,当建筑物的数量是0的时候,直接返回空数组;
当建筑物的数量是1的时候,直接返回[[buildings[0][0], buildings[0][2]], [buildings[0][1], 0]](也就是左上角点和右下角点)。
class Solution:
def getSkyline(self, buildings):
if not buildings:
return []
if len(buildings) == 1:
return [[buildings[0][0], buildings[0][2]], [buildings[0][1], 0]]
mid = len(buildings) // 2
left = self.getSkyline(buildings[:mid])
right = self.getSkyline(buildings[mid:])
return self.merge(left, right)
def merge(self, left, right):
lh = rh = l = r = 0
res = []
while l < len(left) and r < len(right):
if left[l][0] < right[r][0]:
cp = [left[l][0], max(left[l][1], rh)]
lh = left[l][1]
l += 1
elif left[l][0] > right[r][0]:
cp = [right[r][0], max(right[r][1], lh)]
rh = right[r][1]
r += 1
else:
cp = [left[l][0], max(left[l][1], right[r][1])]
lh, rh = left[l][1], right[r][1]
l += 1
r += 1
if len(res) == 0 or res[-1][1] != cp[1]:
res.append(cp)
res += left[l:] + right[r:]
return res
v1-暴力算法
TBC…
思路
小结
参考资料
https://leetcode.cn/problems/the-skyline-problem/description/
