11. 盛最多水的容器 Container With Most Water
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
例子
示例 1:
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
```
## 提示:
n == height.length
2 <= n <= 10^5
0 <= height[i] <= 10^4
# V1-基本算法
## 思路
最简单的,我们直接两次迭代,找到所有的 [i, j] 组合,计算所有的面积,招到最大的即可。
高度:每次取高度,取最低的。(木桶理论)
宽度:水墙壁的宽度忽略,相邻2个间距为下标的差。
## java 实现
```java
public int maxArea(int[] height) {
int maxResult = -1;
for(int i = 0; i < height.length; i++) {
for(int j = 0; j < height.length; j++) {
// 跳过自身相等的元素
if(i == j) {
continue;
}
int hi = height[i];
int hj = height[j];
// 高度取最小的
int min = Math.min(hi, hj);
int x = Math.abs(j - i);
int area = x * min;
if(area > maxResult) {
maxResult = area;
}
}
}
return maxResult;
}
效果
Runtime: 843 ms, faster than 5.04% of Java online submissions for Container With Most Water.
Memory Usage: 39.4 MB, less than 94.66% of Java online submissions for Container With Most Water.
很慢。
那么能不能优化呢?
简单优化
我们可以针对迭代进行优化,保障 j > i。
但是变化不大,所以不认为是一个单独的算法:
/**
* 优化思路
*
* 1. 避免重复计算
* 2. j 永远大于 i,跳过计算
* @param height 高度数组
* @return 结果
* @since v2
*/
public int maxAreaV2(int[] height) {
int maxResult = -1;
for(int i = 0; i < height.length; i++) {
for(int j = i+1; j < height.length; j++) {
int hi = height[i];
int hj = height[j];
int min = Math.min(hi, hj);
int x = j-i;
int area = x * min;
if(area > maxResult) {
maxResult = area;
}
}
}
return maxResult;
}
V2-双指针法
思路
首先从 l=0, r=height.length-1(两边)
(1)比较二者数字大小
if(height[l] < height[r]) {
// 左边小,那么高度被固定,右边移动已经达到最大。只能左边向右移动
} else {
// 右边下,右边高度被固定,只能最右往左移动。
}
(2)终止条件
l >= R 则终止。
(3)优化点
因为每次只移动一位,所以不需要每次都采用减法,直接使用变量保存即可。
大小比较实用内部方法,而不是 Math 的方法。
PS: 实践证明,内部方法确实比 Math 的快。不过一般没必要,这个属于极限优化,一个小技巧。
java 实现
public int maxArea(int[] height) {
int l = 0;
int r = height.length-1;
int maxArea = 0;
int width = height.length-1;
while (l < r) {
int area = min(height[l], height[r]) * (width);
maxArea = max(area, maxArea);
// 考虑如何移动指针
if(height[l] >= height[r]) {
// 左边比较大
r--;
} else {
l++;
}
width--;
}
return maxArea;
}
private int min(int a, int b) {
return a < b ? a : b;
}
private int max(int a, int b) {
return a > b ? a : b;
}
效果
TC 从 O(N^2) 降低到 O(N),非常强的算法。
虽然看起来平平无奇,后续的解题中也会用到。
Runtime: 2 ms, faster than 95.28% of Java online submissions for Container With Most Water.
Memory Usage: 40 MB, less than 38.16% of Java online submissions for Container With Most Water.
小结
第一种算法,应该很容易考虑到。
双指针法,是一种从两边开始,同时向中间移动的,非常好用的算法。
使用内部方法提升性能,也是一个不错的小技巧。
42. 接雨水 Trapping Rain Water
题目
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length
1 <= n <= 2 * 10^4
0 <= height[i] <= 10^5
v1-按列计算
思路
我们从左到右,求每一列的水,总和就是结果。
1)第一列和最后一列都是 0
2)中间列的水要怎么求?
当求中间列 i 的时候 , 要知道左边 [0, i) 最高的列 hl,和右边 [i+1, len-1) 最高的列 hr。
因为下雨的时候,雨水一定在左右两边最高的范围内,根据木桶理论,水位的高度取决于短板。也就是 h_min = min(hl, hr)。
所以当前列只有高度低于 h 的时候,对应的存储水位 h_min - h_i
知道这些,代码实现起来并不难。
java 实现
public int trap(int[] height) {
int n = height.length;
// 第一个,最后一列不用看。
int sum = 0;
for(int i = 1; i < n-1; i++) {
int hl = getMaxHeight(height, 0, i-1);
int hr = getMaxHeight(height, i+1, n-1);
int h = Math.min(hl, hr);
if(height[i] < h) {
sum += (h - height[i]);
}
}
return sum;
}
private int getMaxHeight(int[] height,
int startIndex,
int endIndex) {
int res = 0;
for(int i = startIndex; i <= endIndex; i++) {
res = Math.max(res, height[i]);
}
return res;
}
复杂度
TC: O(N^)
MC: O(1)
321 / 322 执行超时。
V2-动态规划
思路-空间换时间
这里面比较大的问题,在于我们计算高度,都是从头开始计算,实际上不需要。
我们可以把数据记录下来。
dp[0] = height[0];
dp[len-1] = height[len-1];
不过需要把上面的方法调整一下,这样和 i 的移动保持一致。
让 hl 的计算从左到右推进,dp[l] = max(dp[l-1], height[l])
让 hr 的计算从右到做推进,dp[r] = max(dp[r+1], height[r])
java 实现
public int trap(int[] height) {
int n = height.length;
// 初始化好对应的高度信息。
int[] dpLeft = new int[n];
dpLeft[0] = height[0];
for(int i = 1; i < n-1; i++) {
dpLeft[i] = Math.max(dpLeft[i-1], height[i]);
}
int[] dpRight = new int[n];
dpRight[n-1] = height[n-1];
for(int i = n-2; i >= 1; i--) {
dpRight[i] = Math.max(dpRight[i+1], height[i]);
}
// 第一个,最后一列不用看。
int sum = 0;
for(int i = 1; i < n-1; i++) {
int hl = dpLeft[i];
int hr = dpRight[i];
int h = Math.min(hl, hr);
if(height[i] < h) {
sum += (h - height[i]);
}
}
return sum;
}
效果
时间/空间复杂度
TC: O(N)
MC: O(N)
TC: 1ms, 98.34%
MC: 42.8mb, 81.49%
只能说,DP YYDS!
v3-双指针
优化左边高度数组
我们的 MC 使用了两个数组,那么有没有办法简化一下呢?
观察 v2 中的,dpLeft 与 遍历处理时的下标一致,而且元素都只临时使用一次。
所以可以把 dpLeft 简化掉。
java 实现 1
public int trap(int[] height) {
int n = height.length;
int[] dpRight = new int[n];
dpRight[n-1] = height[n-1];
for(int i = n-2; i >= 1; i--) {
dpRight[i] = Math.max(dpRight[i+1], height[i]);
}
// 第一个,最后一列不用看。
int sum = 0;
int hl = height[0];
for(int i = 1; i < n-1; i++) {
hl = Math.max(hl, height[i]);
int hr = dpRight[i];
int h = Math.min(hl, hr);
if(height[i] < h) {
sum += (h - height[i]);
}
}
return sum;
}
这里 dpLeft 数组被简化掉了。
那么,我们可以进一步优化掉 dpRight 数组吗?
优化右边高度数组的思路-双指针
没法简单的移除 dpRight 的原因是,dpLeft 和我们的遍历顺序一致,但是 dpRight 是反过来的。
所以这里要用到两个指针,left 和 right,从两个方向去遍历。
那么什么时候从左到右,什么时候从右到左呢?根据下边的代码的更新规则,我们可以知道
使用双指针(左右两边各两个指针)
我们使用一根一根柱子计算装水量的方法
left 表示左边当前遍历的柱子(即左边我们需要计算能够装多少水的柱子)
leftMax 表示 left 的左边最高的柱子长度(不包括 left)
right 表示右边当前遍历的柱子
rightMax 表示 right 的右边最高的柱子长度(不包括 right)
我们有以下几个公式:
当 leftMax < rightMax 的话,那么我们就判断 leftMax 是否比 left 高
因为根据木桶效应,一个桶装水量取决于最短的那个木板,这里也一样,柱子能否装水取决于左右两边的是否都存在比它高的柱子
因为 leftMax < rightMax 了,那么我们只需要比较 leftMax 即可
如果 leftMax > left,那么装水量就是 leftMax - left
如果 leftMax <= left,那么装水量为 0,即 left 装不了水
当 leftMax >= rightMax 的话,同理如上,比较 rightMax 和 right
???? 为什么 rightMax 和 left 隔这么远我们还可以使用 rightMax 来判断?
前提:leftMax < rightMax
rightMax 虽然跟 left 离得远,但有如下两种情况:
1、left 柱子和 rightMax 柱子之间,没有比 rightMax 柱子更高的柱子了,
那么情况如下: left 能否装水取决于 leftMax 柱子是否比 left 高
|
| |
| | |
↑ ↑ ↑
l_m l r_m
2、left 柱子和 rightMax 柱子之间存在比 rightMax 柱子更高的柱子
那么情况如下:因为存在了比 rightMax 更高的柱子,那么我们仍然只需要判断 leftMax 是否比 left 高,因为右边已经存在比 left 高的柱子 | | | | | | | | | | ↑ ↑ ↑ ↑ l_m l mid r_m
初始化指针:
left = 1;
right = len - 2;
leftMax = 0;
rightMax = len - 1;
(因为第一个柱子和最后一个柱子肯定不能装水,因为不作为装水柱子,而是作为左边最高柱子和右边最高柱子)
java 实现
这里使用 while 更能体会到双指针的妙处。
木桶理论:最大水量,取决于短板。
public int trap(int[] height) {
int n = height.length;
//1. 最大高度
int left = 0;
int right = n-1;
int maxLeft = height[left];
int maxRight = height[right];
int sum = 0;
while (left <= right) {
// 取决于左边
if(maxLeft < maxRight) {
if(height[left] > maxLeft) {
// 无法蓄水
maxLeft = height[left];
} else {
// 可以蓄水
sum += maxLeft - height[left];
}
// 左边指针往右移动
left++;
} else {
// 取决于右边
if(height[right] > maxRight) {
// 无法蓄水
maxRight = height[right];
} else {
// 可以蓄水
sum += maxRight - height[right];
}
// 右边指针往左移动
right--;
}
}
return sum;
}
复杂度
TC: O(N)
MC: O(1)
评价
老实说,双指针确实是性能与空间的最佳,但是比较难想,而且容易出错。
407. 接雨水 II
题目
给你一个 m x n 的矩阵,其中的值均为非负整数,代表二维高度图每个单元的高度,请计算图中形状最多能接多少体积的雨水。
示例
示例 1:

输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
输出: 4
解释: 下雨后,雨水将会被上图蓝色的方块中。总的接雨水量为1+2+1=4。
示例 2:
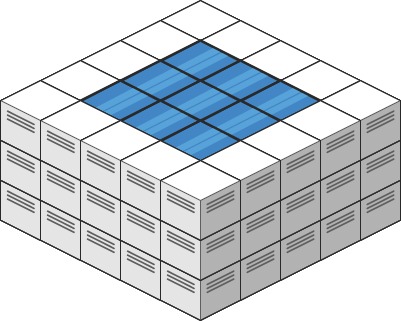
输入: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
输出: 10
```
### 提示:
m == heightMap.length
n == heightMap[i].length
1 <= m, n <= 200
0 <= heightMap[i][j] <= 2 * 10^4
## 思路
下面的一些知识准备,感兴趣可以看一下,便于理解。
> [优先级队列与堆排序 PriorityQueue & heap sort](https://houbb.github.io/2019/01/04/prority-queue)
> [图最短路径算法之迪杰斯特拉算法(Dijkstra)](https://houbb.github.io/2020/01/23/data-struct-learn-03-graph-dijkstra)
------------------------------------------------------------------------------------------------------------------------
接雨水I中,我们维护了左右两个最高的墙,那么在这里,就是维护周围一个圈,用堆来维护周围这一圈中的最小元素。
为什么是维护最小的元素不是最大的元素呢,因为木桶原理呀。
这个最小的元素从堆里弹出来,和它四个方向的元素去比较大小,看能不能往里灌水,怎么灌水呢,如果用方向就比较复杂了,我们可以用visited数组来表示哪些遍历过,哪些没遍历过。
如果当前弹出来的高度比它周围的大,他就能往矮的里面灌水了,灌水后要把下一个柱子放进去的时候,放的高度要取两者较大的,也就是灌水后的高度,不是它原来矮的时候的高度了,如果不能灌水,继续走。
Given the following 3x6 height map: [ [1,4,3,1,3,2], [3,2,1,3,2,4], [2,3,3,2,3,1] ]
就拿这个例子来说,我们先把第一圈都放进去,然后开始从堆中弹出,第一圈,最小值是1(遍历时候标记为访问过),1从堆里弹出来,比如弹出来1(坐标[0,3]),它下方的3没有被访问过,尝试灌水,发现不能灌水,3入堆,然后继续弹。比如说,我此时弹出来一个3(坐标[1,0]),它能向右边2(坐标[1,1])灌水,那这边就可以统计了,然后我们要插入2(坐标[1,1])这个位置,但是插入的时候,要记得你得是插入的高度得是灌水后的高度,而不是原来的高度了。
补充一下评论区的信息:
/**
- 把每一个元素称作块。因为那个图片给的好像瓷砖啊。
- 其实做这题一开始都是想的是对于每一个块,去找它四个方向最高的高度中的最小值(二维下则是左右最高的高度取较小的那一个)作为上界,当前块作为下界 但是这4个方向每次遍历复杂度过高,且不能像二维那样去提前预存每个方向的最大值
- 那可以反过来我不以每个块为处理单元,而是以块的四周作为处理单元
- 那如何保证所有四周的可能性都考虑到呢? 我们从矩阵的最外围往里面遍历,像一个圈不断缩小的过程
- 为了防止重复遍历用visited记录
- 其次要用小顶堆(以高度为判断基准)来存入所有快的四周(即圈是不断缩小的,小顶堆存的就是这个圈)
- 为什么要用小顶堆? 这样可以保证高度较小的块先出队
** 为什么要让高度较小的块先出队?(关键点)
- 一开始时候就讲了基础做法是:对于每一个块,去找它四个方向最高的高度中的最小值(二维下则是左右最高的高度取较小的那一个)作为上界,当前块作为下界
- 而我们现在反过来不是以中心块为处理单元,而是以四周作为处理单元
- 我们如果能确保当前出队的元素对于该中心块来说是它周围四个高度中的最小值那么就能确定接雨水的大小
- 为什么队头元素的高度比中心块要高它就一定是中心块周围四个高度中的最小值呢? 因为我们的前提就是小顶堆:高度小的块先出队,所以对于中心块来说,先出队的必然是中心块四周高度最小的那一个
- 步骤:
- 构建小顶堆,初始化为矩阵的最外围(边界所有元素)
- 不断出队,倘若队头元素的四周(队头元素的四周其实就是上面说的中心块,队头元素是中心块的四周高度中最矮的一个) 即代表能够接雨水:队头元素减去该中心块即当前中心块能接雨水的值
- 但是接完雨水之后中心块还要存进队列中,但这时要存入的中心块是接完雨水后的中心块 */ ```
java 实现
个人理解:
(1)visit 数组,标记是否访问过。
(2)使用优先级队列,初始化的时候,把最外边一圈放进去。保障每次出栈的是最小值
(3)方向处理很巧妙,把四个方向,用一个数组搞定。
(4)处理逻辑:
不断出队,倘若队头元素的四周(队头元素的四周其实就是上面说的中心块,队头元素是中心块的四周高度中最矮的一个)即代表能够接雨水:队头元素减去该中心块即当前中心块能接雨水的值
但是接完雨水之后中心块还要存进队列中,但这时要存入的中心块是接完雨水后的中心块
class Solution {
public int trapRainWater(int[][] heights) {
if (heights == null || heights.length == 0) return 0;
int n = heights.length;
int m = heights[0].length;
// 用一个vis数组来标记这个位置有没有被访问过
boolean[][] vis = new boolean[n][m];
// 优先队列中存放三元组 [x,y,h] 坐标和高度
PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> o1[2] - o2[2]);
// 先把最外一圈放进去
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (i == 0 || i == n - 1 || j == 0 || j == m - 1) {
pq.offer(new int[]{i, j, heights[i][j]});
vis[i][j] = true;
}
}
}
int res = 0;
// 方向数组,把dx和dy压缩成一维来做
int[] dirs = {-1, 0, 1, 0, -1};
while (!pq.isEmpty()) {
int[] poll = pq.poll();
// 看一下周围四个方向,没访问过的话能不能往里灌水
for (int k = 0; k < 4; k++) {
int nx = poll[0] + dirs[k];
int ny = poll[1] + dirs[k + 1];
// 如果位置合法且没访问过
if (nx >= 0 && nx < n && ny >= 0 && ny < m && !vis[nx][ny]) {
// 如果外围这一圈中最小的比当前这个还高,那就说明能往里面灌水啊
if (poll[2] > heights[nx][ny]) {
res += poll[2] - heights[nx][ny];
}
// 如果灌水高度得是你灌水后的高度了,如果没灌水也要取高的
pq.offer(new int[]{nx, ny, Math.max(heights[nx][ny], poll[2])});
vis[nx][ny] = true;
}
}
}
return res;
}
}
复杂度
TC: O(MNlog(MN))
我们需要将矩阵中的每个元素都进行遍历,同时将每个元素都需要插入到优先队列中,总共需要向队列中插入 MN 个元素。每次堆调整的复杂度为 O(log(MN))
MC: O(MN) 需要创建额外的空间对元素进行标记
开源地址
为了便于大家学习,所有实现均已开源。欢迎 fork + star~
参考资料
https://leetcode.cn/problems/container-with-most-water/
https://leetcode.cn/problems/trapping-rain-water/
https://leetcode.cn/problems/trapping-rain-water/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-w-8/
https://leetcode.com/problems/trapping-rain-water-ii/description/
https://leetcode.cn/problems/trapping-rain-water-ii/solution/gong-shui-san-xie-jing-dian-dijkstra-yun-13ik/
https://leetcode.cn/problems/trapping-rain-water-ii/solution/you-xian-dui-lie-de-si-lu-jie-jue-jie-yu-shui-ii-b/
https://leetcode.cn/problems/trapping-rain-water-ii/solution/jie-yu-shui-ii-by-leetcode-solution-vlj3/
