20. 有效的括号
题目
给定一个只包括 ()[]{} 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
-
左括号必须用相同类型的右括号闭合。
-
左括号必须以正确的顺序闭合。
-
每个右括号都有一个对应的相同类型的左括号。
例子
示例 1:
输入:s = “()” 输出:true
示例 2:
输入:s = “()[]{}” 输出:true
示例 3:
输入:s = “(]” 输出:false
提示:
1 <= s.length <= 10^4
s 仅由括号 ‘()[]{}’ 组成
V1-基于 Stack
思路
这一道题作为 22 题的开胃菜,实现起来也不难。
我们可以直接使用 stack 存入元素,每次遇到开头的 ([{ 则进行入栈,遇到 )]} 则进行出栈,并且要求一一对应。
java 实现
import java.util.HashMap;
import java.util.Map;
import java.util.Stack;
/**
* @author d
* @since 1.0.0
*/
public class T020_ValidParentheses {
private static final Map<Character, Character> MAP = new HashMap<>(4);
static {
MAP.put(')', '(');
MAP.put('}', '{');
MAP.put(']', '[');
}
/**
* 简单思路
* @param s 字符串
* @return 结果
* @since v1
*/
public boolean isValid(String s) {
if(null == s || s.length() == 0) {
return true;
}
// 奇数
if(s.length() % 2 != 0) {
return false;
}
Stack<Character> stack = new Stack<>();
for(int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if(c == '(' || c == '{' || c == '[') {
stack.push(c);
} else {
// 开始 pop
if(stack.isEmpty()) {
return false;
}
char pop = stack.pop();
char expectPop = MAP.get(c);
if(pop != expectPop) {
return false;
}
}
}
return stack.isEmpty();
}
}
效果
Runtime: 1 ms, faster than 98.79% of Java online submissions for Valid Parentheses.
Memory Usage: 37.4 MB, less than 70.07% of Java online submissions for Valid Parentheses.
v2-模拟 stack
思路
我们在通过 stack 的时候,实际上也可以使用数组模拟实现。
这样代码看起来更加简单一些。
java 实现
/**
* 大道至简
*
* @param s 字符串
* @return 结果
* @since v1
*/
public boolean isValid(String s) {
int length = s.length();
char[] stack = new char[length];
int headIx = 0;
for(int i = 0; i < length; i++) {
char c = s.charAt(i);
switch (c) {
case '{':
case '[':
case '(':
stack[headIx++] = c;
break;
case '}':
if(headIx == 0 || stack[--headIx] != '{') {
return false;
}
break;
case ']':
if(headIx == 0 || stack[--headIx] != '[') {
return false;
}
break;
case ')':
if(headIx == 0 || stack[--headIx] != '(') {
return false;
}
break;
}
}
return headIx == 0;
}
效果
Runtime: 0 ms, faster than 100.00% of Java online submissions for Valid Parentheses.
Memory Usage: 37.1 MB, less than 95.67% of Java online submissions for Valid Parentheses.
22. 括号生成
题目
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且有效的括号组合。
示例:
输入:n = 3 输出:[ “((()))”, “(()())”, “(())()”, “()(())”, “()()()” ]
思路分析
你看这道题,他的样子平淡无奇。
但是既然我们选择讲解,那他一定有自己的不凡之处,下面我们来逐层学习这道题背后解法。
题目在于精,而不在于多,可以举一反三,自然胜过走马观花。
思路1-暴力破万法
忘记在哪里看到的一句话,计算机实际上只会一种策略——穷举,所有的算法只是教会其如何更加聪明的穷举而已。
首先,我们来看一种最简单粗暴的方式。
流程
-
构建所有
()可能构成的字符串 -
过滤出其中符合条件的字符串。
示例代码
/**
*
* 思路:
*
* (1)生成所有可能
* (2)如果符合则加入结果
*
* @param n 数字
* @return 结果
*/
public List<String> generateParenthesis(int n) {
List<String> all = generateAll(n);
List<String> resultList = new ArrayList<>();
for(String string : all) {
if(isValid(string)) {
resultList.add(string);
}
}
return resultList;
}
/**
* 生成所有的可能字符串
* @param n 个数
* @return 结果
*/
private List<String> generateAll(final int n) {
List<String> resultList = new ArrayList<>();
resultList.add("");
char[] chars = new char[]{'(', ')'};
for(int i = 0; i < n*2; i++) {
List<String> newList = new ArrayList<>();
for(String result : resultList) {
for(char c: chars) {
newList.add(result+c);
}
}
resultList = newList;
}
return resultList;
}
/**
* 是否合法
* @param s 字符串
* @return 结果
*/
private boolean isValid(final String s) {
int length = s.length();
int headIx = 0;
for(int i = 0; i < length; i++) {
char c = s.charAt(i);
if('(' == c) {
headIx++;
} else {
if(headIx == 0) {
return false;
}
headIx--;
}
}
return headIx == 0;
}
性能
这个方法提交,结果评测只能超过 5.08% 的实现,太惨了!
这是乌龟妈妈开门——慢到家了。
那么问题出在哪里呢?其实就是这种穷举太笨了,没有一点选择性。
思路2-DFS 深度优先遍历
我们考虑 n=2 的情况,即 left 表示“左括号还有几个没有用掉”,right 表示“右括号还有几个没有用掉”,可以画出一棵递归树。
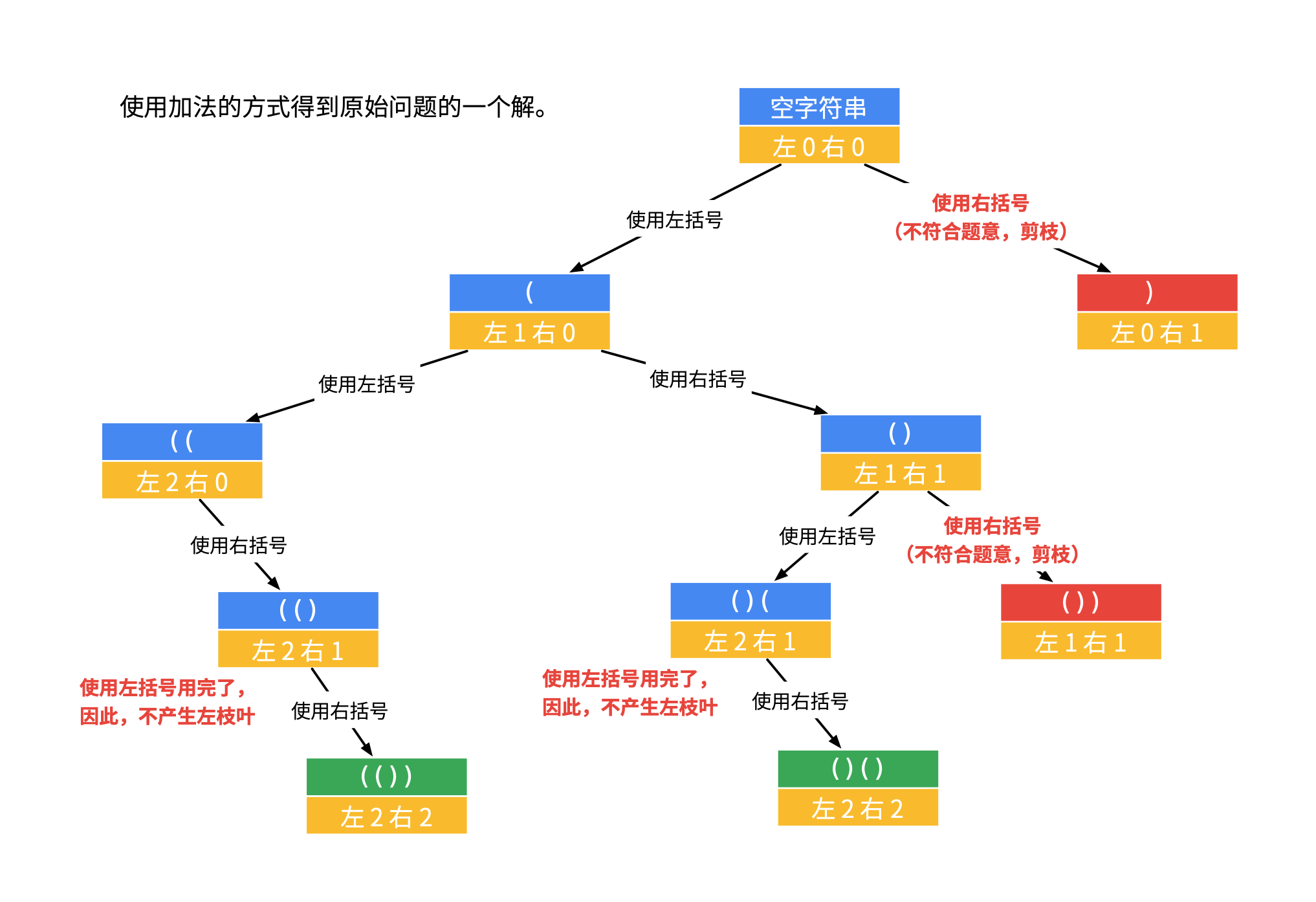
这里我们可以很明显的做一些剪枝算法,把不可能的情况提前过滤掉。
流程
-
第一个有效符号一定是
( -
(个数比)少的时候,进行剪枝 -
(和)的个数都等于 n 的时候,一次遍历就结束了。
实现
public List<String> generateParenthesis(int n) {
List<String> resultList = new ArrayList<>();
dfs(resultList, "", 0, 0, n);
return resultList;
}
/**
* 深度优先遍历
* @param resultList 结果列表
* @param string 字符串
* @param left 左括号
* @param right 右括号
* @param num 位数
*/
private void dfs(List<String> resultList,
String string,
int left,
int right,
int num) {
if(left == num && right == num) {
resultList.add(string);
return;
}
//左边的括号是可以一直加的
if(left < num) {
dfs(resultList, string+"(", left+1, right, num);
}
// 这里是对剪枝处理的优化,如果 left < right,是跳过的。
// ) 小于 < 的时候,可以添加
if(right < left) {
dfs(resultList, string+")", left, right+1, num);
}
}
性能
Runtime: 1 ms, faster than 85.42% of Java online submissions for Generate Parentheses.
Memory Usage: 39 MB, less than 98.86% of Java online submissions for Generate Parentheses.
这里超越了 85% 的实现,但是作为算法题解,我们是不满意的。
那么问题出在哪里呢?
实际上 String 有过多次的隐式创建,还是很消耗性能的。我们来做一个改良版本。
思路3-DFS 深度优先遍历改进
实现
其实这里才算是一个标准的回溯算法。
核心区别就是我们使用 StringBuilder 替代了 String,注意这里是需要重新设置长度的,这样才能保证回溯正确。
public List<String> generateParenthesis(int n) {
List<String> resultList = new ArrayList<>();
StringBuilder stringBuilder = new StringBuilder(n << 1);
backtrack(resultList, stringBuilder, 0, 0, n);
return resultList;
}
/**
* 递归处理
* @param resultList 结果列表
* @param stringBuilder 字符串
* @param left 左括号
* @param right 右括号
* @param num 位数
*/
private void backtrack(List<String> resultList,
StringBuilder stringBuilder,
int left,
int right,
int num) {
if(stringBuilder.length() == num << 1) {
resultList.add(stringBuilder.toString());
return;
}
//左边的括号是可以一直加的
if(left < num) {
backtrack(resultList, stringBuilder.append("("), left+1, right, num);
// 重新设置
stringBuilder.setLength(stringBuilder.length()-1);
}
// ) 小于 < 的时候,可以添加
if(right < left) {
backtrack(resultList, stringBuilder.append(")"), left, right+1, num);
stringBuilder.setLength(stringBuilder.length()-1);
}
}
性能
超越了 100% 的 java 实现,这次算是基本满意了。
实际上还是有些地方可以优化的,比如列表扩容等等,此处不再展示。
Runtime: 0 ms, faster than 100.00% of Java online submissions for Generate Parentheses.
Memory Usage: 39.6 MB, less than 63.29% of Java online submissions for Generate Parentheses.
看到这里你可能会想,终于结束了,这道题还有点意思。
少侠留步,为了举一反三,本文还将讨论下此类问题的其他几种解法。
让你感受一下,一题更比六题强的快乐~
思路4-DFS 深度优先方式2
上面主要展示了 DFS 做加法的方式,其实也可以反过来做减法。
整体大同小异,和思路 2 比较类似,此处保留主要是为了提供更多的角度。
整体图示:
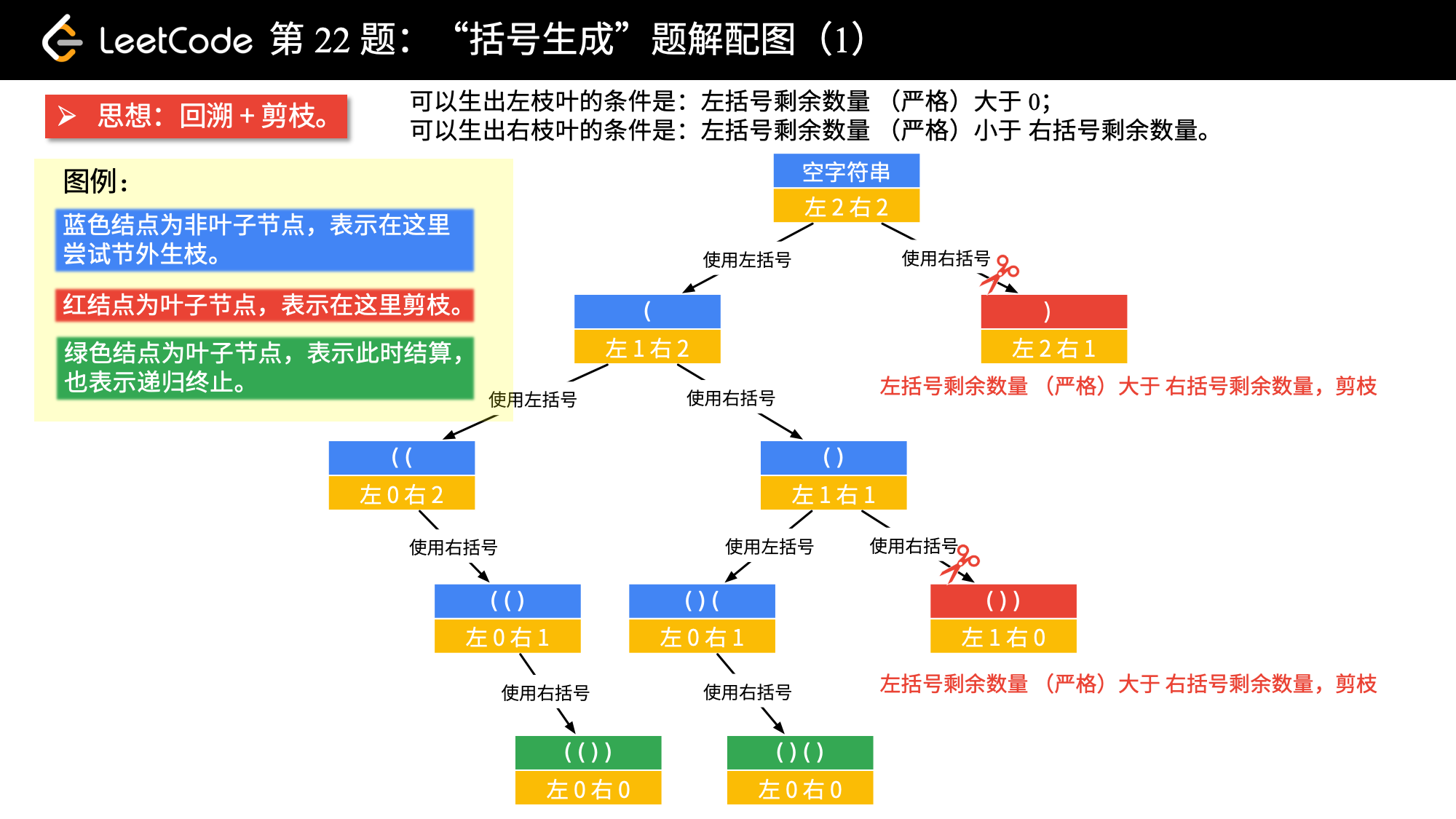
java 实现
public List<String> generateParenthesis(int n) {
List<String> resultList = new ArrayList<>();
dfs(resultList, "", n, n, n);
return resultList;
}
/**
* 深度优先遍历
* @param resultList 结果列表
* @param string 字符串
* @param left 左括号
* @param right 右括号
* @param num 位数
*/
private void dfs(List<String> resultList,
String string,
int left,
int right,
int num) {
if(left == 0 && right == 0) {
resultList.add(string);
return;
}
// 剪枝(左括号可以使用的个数严格大于右括号可以使用的个数)
if (left > right) {
return;
}
if(left > 0) {
dfs(resultList, string+"(", left-1, right, num);
}
if(right > 0) {
dfs(resultList, string+")", left, right-1, num);
}
}
思路5-BFS 广度优先遍历
说到 DFS,那么自然而然可以想到 BFS。
不过 BFS 需要我们自己去处理一下节点,用起来感觉没有 DFS 递归方便,此处也记录一下,拓展一下思路。
或者你遇到了指定用 BFS 去解决的题目:
java 实现
这里采用自定义 Node 节点,然后横向优先遍历的方式。
class Node {
private String text;
private int left;
private int right;
public Node(String text, int left, int right) {
this.text = text;
this.left = left;
this.right = right;
}
}
/**
* @param n 数字
* @return 结果
*/
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<>();
if (n == 0) {
return res;
}
// 从上到下
Queue<Node> queue = new LinkedList<>();
Node rootNode = new Node("", 0, 0);
queue.add(rootNode);
while (!queue.isEmpty()) {
Node curNode = queue.remove();
// 最后一层
if (curNode.left == n && curNode.right == n) {
res.add(curNode.text);
}
if (curNode.left < n) {
queue.add(new Node(curNode.text + "(", curNode.left + 1, curNode.right));
}
// 剪枝
if (curNode.right < curNode.left) {
queue.add(new Node(curNode.text + ")", curNode.left, curNode.right + 1));
}
}
return res;
}
当然这里你可以自己实现基于栈 DFS 遍历,此处不再赘述。
思路6-DP 动态规划
动态规划,永远滴神~
此处直接参考 leetcode 官方解法。
核心思路
任何一个括号序列都一定是由 ( 开头,并且第一个 ( 一定有一个唯一与之对应的 )。
这样一来,每一个括号序列可以用 (a)b 来表示,其中 a 与 b 分别是一个合法的括号序列(可以为空)。
那么,要生成所有长度为 2 * n 的括号序列,我们定义一个函数 generate(n) 来返回所有可能的括号序列。
那么在函数 generate(n) 的过程中:
-
我们需要枚举与第一个 ( 对应的 ) 的位置 2 * i + 1;
-
递归调用 generate(i) 即可计算 a 的所有可能性;
-
递归调用 generate(n - i - 1) 即可计算 b 的所有可能性;
-
遍历 a 与 b 的所有可能性并拼接,即可得到所有长度为 2 * n 的括号序列。
为了节省计算时间,我们在每次 generate(i) 函数返回之前,把返回值存储起来,下次再调用 generate(i) 时可以直接返回,不需要再递归计算。
ps: DP 最核心的两点
(1)找到递推公式
(2)缓存结果,避免重复计算
java 实现
public List<String> generateParenthesis(int n) {
// 存放缓存信息
List<List<String>> cache = new ArrayList<>();
// 初始化第一个元素列表为 [""]
cache.add(Collections.singletonList(""));
for (int i = 1; i <= n; i++) {
List<String> cur = new ArrayList<>();
for (int j = 0; j < i; j++) {
List<String> str1 = cache.get(j);
List<String> str2 = cache.get(i - 1 - j);
for (String s1 : str1) {
for (String s2 : str2) {
// 枚举右括号的位置
cur.add("(" + s1 + ")" + s2);
}
}
}
cache.add(cur);
}
return cache.get(n);
}
性能
不过这种算法实际执行效果却比较差:
Runtime: 7 ms, faster than 13.20% of Java online submissions for Generate Parentheses.
Memory Usage: 39.5 MB, less than 65.23% of Java online submissions for Generate Parentheses.
小结
类似的这种二叉树遍历问题,其实都可以使用 DFS/BFS,可以使用递归,也可以使用栈/队列实现。
针对本题,可以使用最笨的暴力算法,也可以通过剪枝降低耗时。
不知道你的收获如何呢?
32. 最长有效括号 Longest Valid Parentheses
题目
给你一个只包含 ‘(‘ 和 ‘)’ 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
例子
示例 1:
输入:s = “(()” 输出:2 解释:最长有效括号子串是 “()”
示例 2:
输入:s = “)()())” 输出:4 解释:最长有效括号子串是 “()()”
示例 3:
输入:s = “” 输出:0
提示:
0 <= s.length <= 3 * 10^4
s[i] 为 ‘(‘ 或 ‘)’
v1-暴力算法
思路
直接截取所有的 s[i,j],判断对应的子串是否为有效的子串。
是否有效直接参考 T20。
java 实现
/**
* 最简单的思路:
*
* 1. 通过双指针,两边移动。截取 substring
* 2. 通过 020 的方法,判断字符串是否为 valid,是返回 j-i
* 3. i j 重合,返回 0
*
* 这种解法:会在 222 CASE 超时
*
* @param s 字符串
* @return 结果
*/
public int longestValidParentheses(String s) {
//0.1 都不是
if(s.length() <= 1) {
return 0;
}
// 这个复杂度是 o(N^3),肯定没戏
for (int stepLen = s.length(); stepLen >= 2; stepLen--) {
// 逆序,本质是双指针
for(int i = 0; i < s.length()-1; i++) {
// fast-return
if(i + stepLen > s.length()) {
break;
}
String subString = s.substring(i, i+stepLen);
if(isValid(subString)) {
return stepLen;
}
}
}
// 没有
return 0;
}
/**
* 大道至简
*
* T020
*
* @param s 字符串
* @return 结果
* @since v1
*/
public static boolean isValid(String s) {
// 奇数个,不可能满足
if(s.length() % 2 != 0) {
return false;
}
Stack<Character> stack = new Stack<>();
for(int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if(c == '(') {
stack.push(c);
} else {
// 开始 pop
if(stack.isEmpty()) {
return false;
}
char pop = stack.pop();
char expectPop = '(';
if(pop != expectPop) {
return false;
}
}
}
return stack.isEmpty();
}
复杂度
这个 TC 为 O(N^3)。外边两层遍历,中间判断合法又是 O(N)。
执行会直接超时。
V2-基于 stack
思路
其实有更加优雅的方式,我们通过 stack 存储。
具体做法是我们始终保持栈底元素为当前已经遍历过的元素中「最后一个没有被匹配的右括号的下标」,这样的做法主要是考虑了边界条件的处理,栈里其他元素维护左括号的下标:
1) 对于遇到的每个 (,我们将它的下标放入栈中
2) 对于遇到的每个 ),我们先弹出栈顶元素表示匹配了当前右括号:
2.1) 如果栈为空,说明当前的右括号为没有被匹配的右括号,我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
2.2) 如果栈不为空,当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」
我们从前往后遍历字符串并更新答案即可。
需要注意的是,如果一开始栈为空,第一个字符为左括号的时候我们会将其放入栈中,这样就不满足提及的「最后一个没有被匹配的右括号的下标」,为了保持统一,我们在一开始的时候往栈中放入一个值为 -1 的元素。
java 实现
class Solution {
public int longestValidParentheses(String s) {
int maxans = 0;
Deque<Integer> stack = new LinkedList<Integer>();
stack.push(-1);
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
stack.push(i);
} else {
stack.pop();
if (stack.isEmpty()) {
stack.push(i);
} else {
maxans = Math.max(maxans, i - stack.peek());
}
}
}
return maxans;
}
}
以 ())((()) 为例子,日志为:
i=0, stack=[0, -1], maxans=0
i=1, stack=[-1], maxans=2
i=2, stack=[2], maxans=2
i=3, stack=[3, 2], maxans=2
i=4, stack=[4, 3, 2], maxans=2
i=5, stack=[5, 4, 3, 2], maxans=2
i=6, stack=[4, 3, 2], maxans=2
i=7, stack=[3, 2], maxans=4
复杂度
TC:O(N)
MC: O(N)
v3-DP 动态规划
思路
结合题目,有 最长 这个字眼,可以考虑尝试使用 动态规划 进行分析。这是一个 最值型 动态规划的题目。
动态规划题目分析的 4 个步骤:
1)确定状态
研究最优策略的最后一步
化为子问题
2)转移方程
根据子问题定义得到
3)初始条件和边界情况
4)计算顺序
首先,我们定义一个 dp 数组,其中第 i 个元素表示以下标为 i 的字符结尾的最长有效子字符串的长度。
确定状态-最后一步
对于最优的策略,一定有最后一个元素 s[i].
所以,我们先看第 i 个位置,这个位置的元素 s[i] 可能有如下两种情况:
1) s[i] == '(' ,这时,s[i] 无法和其之前的元素组成有效的括号对,所以,dp[i] = 0
2) s[i] == ')',这时,需要看其前面对元素来判断是否有有效括号对。
2.1) 情况1:
s[i - 1] == '(',即 s[i] 和 s[i - 1] 组成一对有效括号,有效括号长度新增长度2,i 位置对最长有效括号长度为 其之前2个位置的最长括号长度加上当前位置新增的2,我们无需知道i-2位置对字符是否可以组成有效括号对。
那么有:
dp[i] = dp[i - 2] + 2
刚好匹配,所以长度+2。再加上前面的 dp[i-2]
2.2) 情况2:
s[i - 1] == ')'
这种情况下,如果前面有和 s[i] 组成有效括号对的字符,即形如 ((...)),这样的话,就要求 s[i - 1] 位置必然是有效的括号对,否则 s[i] 无法和前面对字符组成有效括号对。
这时,我们只需要找到和 s[i] 配对对位置,并判断其是否是 ( 即可。和其配对对位置为:i - dp[i - 1] - 1。
如果:s[i - dp[i - 1] - 1] == '(',有效括号长度新增长度 2,i 位置对最长有效括号长度为 i-1 位置的最长括号长度加上当前位置新增的 2,那么有:
dp[i] = dp[i - 1] + 2
值得注意的是,i - dp[i - 1] - 1 和 i 组成了有效括号对,这将是一段独立的有效括号序列,如果之前的子序列是形如 (...)(...) 这种序列,那么当前位置的最长有效括号长度还需要加上这一段。
所以:
dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2
子问题
根据上面的分析,我们得到了如下两个计算公式:
dp[i] = dp[i - 2] + 2
dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2
这样状态也明确了:
设 dp 数组,其中第 i 个元素表示以下标为 i 的字符结尾的最长有效子字符串的长度。
转移方程
if s[i] == '(' :
dp[i] = 0
if s[i] == ')' :
if s[i - 1] == '(' :
dp[i] = dp[i - 2] + 2 #要保证i - 2 >= 0
if s[i - 1] == ')' and s[i - dp[i - 1] - 1] == '(' :
dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2 #要保证i - dp[i - 1] - 2 >= 0
初始条件和边界情况:
初始条件:dp[i] = 0
边界情况:需要保证计算过程中:i - 2 >= 0 和 i - dp[i - 1] - 2 >= 0
计算顺序:
无论第一个字符是什么,都有:dp[0] = 0
然后依次计算:dp[1], dp[2], …, dp[n - 1]
结果是: max(dp[i])
java 实现
class Solution {
public int longestValidParentheses(String s) {
int maxans = 0;
int[] dp = new int[s.length()];
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i) == ')') {
if (s.charAt(i - 1) == '(') {
dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
} else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
}
maxans = Math.max(maxans, dp[i]);
}
}
return maxans;
}
}
ps: 这个递推公式比较难,比较容易出错。
复杂度计算:
时间复杂度: 遍历了一遍字符串,所以时间复杂度是:O(N)
空间复杂度:需要和字符串长度相同的数组保存每个位置的最长有效括号长度,所以空间复杂度是:O(N)
V4-正向逆向结合
思路
在此方法中,我们利用两个计数器 left 和 right。首先,我们从左到右遍历字符串,对于遇到的每个 (,我们增加 left 计数器,对于遇到的每个 ),我们增加 right计数器。
每当 left 计数器与 right计数器相等时,我们计算当前有效字符串的长度,并且记录目前为止找到的最长子字符串。
当 right计数器比 left 计数器大时,我们将 left 和 right计数器同时变回 0。
这样的做法贪心地考虑了以当前字符下标结尾的有效括号长度,每次当右括号数量多于左括号数量的时候之前的字符我们都扔掉不再考虑,重新从下一个字符开始计算,但这样会漏掉一种情况,就是遍历的时候左括号的数量始终大于右括号的数量,即 (() ,这种时候最长有效括号是求不出来的。
解决的方法也很简单,我们只需要从右往左遍历用类似的方法计算即可,只是这个时候判断条件反了过来:
1) 当 left 计数器比 right计数器大时,我们将 left 和 right计数器同时变回 0
2) 当 left 计数器与 right计数器相等时,我们计算当前有效字符串的长度,并且记录目前为止找到的最长子字符串
这样我们就能涵盖所有情况从而求解出答案。
java 实现
public int longestValidParentheses(String s) {
int left = 0, right = 0, maxlength = 0;
// 从左往右
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
left++;
} else {
right++;
}
if (left == right) {
maxlength = Math.max(maxlength, 2 * right);
} else if (right > left) {
left = right = 0;
}
}
// 从右往左
left = right = 0;
for (int i = s.length() - 1; i >= 0; i--) {
if (s.charAt(i) == '(') {
left++;
} else {
right++;
}
if (left == right) {
maxlength = Math.max(maxlength, 2 * left);
} else if (left > right) {
left = right = 0;
}
}
return maxlength;
}
复杂度
TC: O(N)
MC: O(1)
开源地址
为了便于大家学习,所有实现均已开源。欢迎 fork + star~
参考资料
https://leetcode.cn/problems/longest-valid-parentheses/solution/zui-chang-you-xiao-gua-hao-by-leetcode-solution/
https://leetcode.cn/problems/longest-valid-parentheses/solution/dong-tai-gui-hua-si-lu-xiang-jie-c-by-zhanganan042/
