77. 组合
题目
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
```
提示:
1 <= n <= 20
1 <= k <= n
## V1-回溯
### 思路
这种全排列,使用回溯实现。整体难度不大。
终止条件:个数为指定的 k
剪枝:如果后面的个数不够了,可以直接返回。
### java 实现
```java
class Solution {
public List<List<Integer>> combine(int n, int k) {
// 这是一道回溯的算法。
List<List<Integer>> results = new ArrayList<>();
List<Integer> tempList = new ArrayList<>(k);
backtrack(results, tempList, n, k, 1);
return results;
}
private void backtrack(List<List<Integer>> results, List<Integer> tempList,
int n, int k, int start) {
// 剪枝算法:效果是非常显著的。
// 如果后面的元素个数已经不够 k 个了,直接返回。
if (tempList.size() + n - start + 1 < k) {
return;
}
// 终止条件
if(tempList.size() == k) {
results.add(new ArrayList<>(tempList));
}
// 从第一个元素开始
// 这个操作是从前向后的,所以前面的元素不会被重复处理。
for(int i = start; i <= n; i++) {
tempList.add(i);
// 从下一个元素开始,不可重复
backtrack(results, tempList, n, k, i+1);
// 回溯
tempList.remove(tempList.size()-1);
}
}
}
效果
TC: 2ms, 95.32%
MC: 40mb, 100%
39. 组合总和
题目
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。
你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
例子
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
```
### 提示:
1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40
## V1-回溯
### 思路
这种需要尝试各种情况的问题,都可以使用回溯来解决。
回溯的模板基本是固定的。
1)定义存放所有结果的列表 resultList
2) 定义回溯方法,传入已知条件 + resultList + 控制下标
3)回溯逻辑
定义好终止条件,满足条件时,把结果加入到 resultList
根据题目条件,选择元素。
递归 + 回溯。
### java 实现
```java
class Solution {
/**
* 思路:
*
* (1)回溯
* (2)剪枝算法优化
*
* @author https://github.com/houbb/
* @param candidates 候选集
* @param target 目标值
* @return 结果
*/
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> results = new ArrayList<>();
backtrack(candidates, target, new ArrayList<>(), 0, results);
return results;
}
private void backtrack(int[] candidates, int remain, List<Integer> tempList,
int begin, List<List<Integer>> results) {
if (remain == 0) {
results.add(new ArrayList<>(tempList));
return;
}
for (int i = begin; i < candidates.length; i++) {
// 这里实际上优化了 2 步:
// 1. candidates 排序并不是必须的
// 2. 单次回溯,根据大小判断,避免一次减法+大小比较
int current = candidates[i];
if (remain >= current) {
tempList.add(current);
// 元素可以重复使用,所以取 i
backtrack(candidates, remain - current, tempList, i, results);
tempList.remove(tempList.size() - 1);
}
}
}
}
这里的元素允许重复使用,所以 i 标识的元素,可以在待选列表中重复选择; 为了避免组合重复,每次 i 要从 begin 位置开始选择。
效果
TC: 2ms, 90.66%
MC: 38.9, 100%
40. 组合总和 II
题目
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次。
注意:解集不能包含重复的组合。
例子
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
v1-基本版本回溯
思路
这一题,和 T39 的区别,就是不允许使用重复元素,其他不变。
如何判断是否使用了重复元素呢?
1)使用 usedNum,存放使用的数字,则跳过。不过这里的输入数字可能重复,不同位置的不算同一个数字。参考例子 1。
2)首先对数组排序,然后组合时,判断 nums[i] === nums[i-1] 则可以跳过这个分支。
java 实现1
通过方式2,解决。
/**
* 思路:
* @author https://github.com/houbb/
* @param candidates 候选集
* @param target 目标值
* @return 结果
*/
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
// 存放使用后的数字
boolean[] used = new boolean[candidates.length];
List<List<Integer>> results = new ArrayList<>();
// 核心算法
backtrack(used,new ArrayList<>(), results, candidates, target, 0);
return results;
}
/**
* 回溯算法
* @param used 使用的数字集合
* @param results 结果
* @param candidates 候选数组
* @param remain 剩余值
* @param begin 开始索引
*/
private void backtrack(boolean[] used,
List<Integer> tempList,
List<List<Integer>> results,
int[] candidates, int remain, int begin) {
if(remain < 0) {
return;
} else if(remain == 0) {
results.add(new ArrayList<>(tempList));
} else {
// 核心处理
for(int i = begin; i < candidates.length; i++) {
int current = candidates[i];
// 避免元素被重复使用
if(used[i]) {
continue;
}
tempList.add(current);
used[i] = true;
backtrack(used, tempList, results, candidates, remain-current, i+1);
used[i] = false;
tempList.remove(tempList.size()-1);
}
}
}
这个处理的结果,会导致数据重复。
例子1会输出:
[[1,2,5],[1,7],[1,6,1],[2,6],[2,1,5],[7,1]]
但是题目中,[1,2,5] 与 [2,1,5] 会认为是相同的解。
我们可以最后统一过滤这种重复的数据:
class Solution {
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
// 存放使用后的数字
boolean[] used = new boolean[candidates.length];
List<List<Integer>> results = new ArrayList<>();
// 核心算法
backtrack(used,new ArrayList<>(), results, candidates, target, 0);
// 统一移除
List<List<Integer>> ans = new ArrayList<>();
for(List<Integer> result : results) {
if(!contains(ans, result)) {
ans.add(result);
}
}
return ans;
}
/**
* 回溯算法
* @param used 使用的数字集合
* @param results 结果
* @param candidates 候选数组
* @param remain 剩余值
* @param begin 开始索引
*/
private void backtrack(boolean[] used,
List<Integer> tempList,
List<List<Integer>> results,
int[] candidates, int remain, int begin) {
if(remain < 0) {
return;
} else if(remain == 0) {
results.add(new ArrayList<>(tempList));
} else {
// 核心处理
for(int i = begin; i < candidates.length; i++) {
int current = candidates[i];
// 避免元素被重复使用
if(used[i]) {
continue;
}
tempList.add(current);
used[i] = true;
backtrack(used, tempList, results, candidates, remain-current, i+1);
used[i] = false;
tempList.remove(tempList.size()-1);
}
}
}
private boolean contains(List<List<Integer>> results,
List<Integer> targetList) {
// 避免修改原始数据
List<Integer> tempList = new ArrayList<>(targetList);
for (List<Integer> list : results) {
// 长度相同
if(isSameCollection(list, tempList)) {
return true;
}
}
return false;
}
private boolean isSameCollection(List<Integer> list,
List<Integer> tempList) {
if(list.size() != tempList.size()) {
return false;
}
Map<Integer, Integer> countMap = new HashMap<>();
for(int i = 0; i < list.size(); i++) {
int countFirst = countMap.getOrDefault(list.get(i), 0) + 1;
countMap.put(list.get(i), countFirst);
int countTemp = countMap.getOrDefault(tempList.get(i), 0) -1;
countMap.put(tempList.get(i), countTemp);
}
for(Map.Entry<Integer, Integer> entry : countMap.entrySet()) {
if(entry.getValue() != 0) {
return false;
}
}
return true;
}
}
不过会在 172 / 176 内存超出。
测试用例:
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
java 实现2
为了解决上面的问题,我们首先对数组进行排序。
if(i > begin && candidates[i] == candidates[i-1]) 如果这个元素和上一个相同,且已经选过了,则跳过。
通过方式1,判断解决。
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
// 这个排序时必须的,用于去重
Arrays.sort(candidates);
List<List<Integer>> results = new ArrayList<>();
// 核心算法
backtrack(results, new ArrayList<>(), candidates, target, 0);
return results;
}
/**
* 回溯算法
* @param results 结果
* @param tempList 临时列表
* @param candidates 候选数组
* @param remain 剩余值
* @param begin 开始索引
* @since v40
*/
private void backtrack(List<List<Integer>> results, List<Integer> tempList,
int[] candidates, int remain, int begin) {
if(remain < 0) {
return;
} else if(remain == 0) {
results.add(new ArrayList<>(tempList));
} else {
// 核心处理
for(int i = begin; i < candidates.length; i++) {
// 如何跳过重复的信息
if(i > begin && candidates[i] == candidates[i-1]) {
continue;
}
int current = candidates[i];
tempList.add(current);
backtrack(results, tempList, candidates, remain-current, i+1);
tempList.remove(tempList.size()-1);
}
}
}
TC: 5ms, 61.49%
MC: 40.6mb, 100%
剪枝优化
我们可以针对上面的回溯,做一点剪枝优化。
private void backtrack(List<List<Integer>> results, List<Integer> tempList,
int[] candidates, int remain, int begin) {
if (remain == 0) {
results.add(new ArrayList<>(tempList));
} else {
// 核心处理
for (int i = begin; i < candidates.length; i++) {
// 如何跳过重复的信息
if (i > begin && candidates[i] == candidates[i - 1]) {
continue;
}
int current = candidates[i];
// 结束当前循环
if (current > remain) {
break;
}
tempList.add(current);
backtrack(results, tempList, candidates, remain - current, i + 1);
tempList.remove(tempList.size() - 1);
}
}
}
因为数组是有序的,后面的越来越大。所以在 current > remain 的时候,后面的就没有必要处理了。
TC: 2ms, 99.85%
MC: 38.8mb, 100%
216. 组合总和 III
题目
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。
示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。
```
提示:
2 <= k <= 9
1 <= n <= 60
## v1-回溯基本版
### 思路
我们可以采用和前面类似的方式。
定义待选数组,为 [1...9] 的数字。
### java 实现 1
```java
public List<List<Integer>> combinationSum3(int k, int n) {
List<List<Integer>> results = new ArrayList<>();
List<Integer> tempList = new ArrayList<>();
int[] nums = new int[]{1,2,3,4,5,6,7,8,9};
backtrack(results, tempList, nums, k, n, 0);
return results;
}
private void backtrack(List<List<Integer>> results,
List<Integer> tempList,
int[] nums,
int k,
int remain,
int start) {
if(remain == 0 && tempList.size() == k) {
results.add(new ArrayList<>(tempList));
return;
}
// 開始的邊界?
for(int i = start; i < nums.length; i++) {
int num = nums[i];
if(tempList.contains(num)) {
continue;
}
// 去重
if(tempList.size() > 0 && num < tempList.get(tempList.size()-1)) {
continue;
}
tempList.add(num);
remain -= num;
backtrack(results, tempList, nums, k, remain, start+1);
// 回溯
tempList.remove(tempList.size()-1);
remain += num;
}
}
效果:
TC: 2ms, 11.23%
MC: 36.3mb, 100%
java 实现2
我们加一个剪枝,当 remain < num 的时候,跳出当前循环。因为 num 都是严格递增的。
private void backtrack(List<List<Integer>> results,
List<Integer> tempList,
int[] nums,
int k,
int remain,
int start) {
if(remain == 0 && tempList.size() == k) {
results.add(new ArrayList<>(tempList));
return;
}
// 開始的邊界?
for(int i = start; i < nums.length; i++) {
int num = nums[i];
if(tempList.contains(num)) {
continue;
}
// 去重
if(tempList.size() > 0 && num < tempList.get(tempList.size()-1)) {
continue;
}
// 剪枝。数字严格递增
if(remain < num) {
break;
}
tempList.add(num);
remain -= num;
backtrack(results, tempList, nums, k, remain, start+1);
// 回溯
tempList.remove(tempList.size()-1);
remain += num;
}
}
效果:
TC: 1ms, 42.7%
MC: 39.7mb, 81.7%
V2-回溯大道至简
思路
不需要 nums 数组,直接变量控制即可。
不需要额外的 remain 变量,直接当做一个值传递即可。而不是在回溯前,加和减。
java 实现
class Solution {
public List<List<Integer>> combinationSum3(int k, int n) {
List<List<Integer>> results = new ArrayList<>();
List<Integer> tempList = new ArrayList<>();
backtrack(results, tempList, k, n, 1);
return results;
}
/**
* 數據重複問題
*
* 3,9
*
* 認爲元素,必須是無順序的。
*
* [[1,2,6],[1,3,5],[1,5,3],[2,3,4],[2,4,3],[3,2,4],[4,2,3]]
* [[1,2,6],[1,3,5],[2,3,4]]
* @param results
* @param tempList
* @param k
* @param remain
* @param start
*/
private void backtrack(List<List<Integer>> results, List<Integer> tempList,
int k, int remain,
int start) {
if(remain == 0 && tempList.size() == k) {
results.add(new ArrayList<>(tempList));
return;
}
// 開始的邊界?
for(int i = start; i < 10; i++) {
tempList.add(i);
backtrack(results, tempList, k, remain-i, i+1);
// 回溯
tempList.remove(tempList.size()-1);
}
}
}
效果
TC: 0ms, 100%
MC: 37mb, 100%
377. 组合总和 Ⅳ
题目
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。
请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
示例
示例 1:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
示例 2:
输入:nums = [9], target = 3
输出:0
v1-回溯
思路
这一题和前面相比,有两个点:
1)允许一个数字被重复使用
2)不同的排列也认为是不同的解
这其实会导致排列的数量爆炸多,比如 [1,2,3],因为 1 可以使用多次。所以就可以一直使用。
java 实现
int count = 0;
public int combinationSum4(int[] candidates, int target) {
backtrack(candidates, target, 0);
return count;
}
/**
* 回溯算法
* @param candidates 候选数组
* @param remain 剩余值
*/
private void backtrack(int[] candidates,
int remain,
int begin) {
// 剪枝
if(remain < 0) {
return;
} else if(remain == 0) {
count++;
} else {
// 核心处理。数据允许重复,不同的排列视为不同的解
for(int i = 0; i < candidates.length; i++) {
int current = candidates[i];
backtrack(candidates, remain-current, begin + 1);
}
}
}
会在 10 / 15 超时。
我们也可以把算法写的更加适合后期调整的方式,复杂度不变:
public int combinationSum4(int[] candidates, int target) {
return backtrack(candidates, target);
}
private int backtrack(int[] candidates, int target) {
//3. Our goal: when currentSum = target
if (0 == target) {
return 1;
}
int res = 0;
//1. Our choices: We can choose a number from the list any number of times and all the numbers
for (int i = 0; i < candidates.length; i++) {
//Our constraints : We can't go beyond target, we can take more element than available in array
int num = candidates[i];
if (target - num >= 0) {
target -= num;
res += backtrack(candidates, target);
//backtrack
target += num;
}
}
return res;
}
v2-回溯+引入缓存
思路
我们引入一个缓存,存放组成每一个数对应的解个数。
避免每次都重复计算。
java 实现
public int combinationSum4(int[] candidates, int target) {
int[] cache = new int[target + 1];
Arrays.fill(cache, -1);
return backtrack(candidates, target, cache);
}
private int backtrack(int[] candidates, int target, int[] cache) {
// 缓存
if(cache[target] != -1) {
return cache[target];
}
//3. Our goal: when currentSum = target
if (0 == target) {
return 1;
}
int res = 0;
//1. Our choices: We can choose a number from the list any number of times and all the numbers
for (int i = 0; i < candidates.length; i++) {
//Our constraints : We can't go beyond target, we can take more element than available in array
int num = candidates[i];
if (target - num >= 0) {
target -= num;
res += backtrack(candidates, target, cache);
//backtrack
target += num;
}
}
// 存放缓存
cache[target] = res;
return res;
}
效果
效果拔群。
TC: 0, 100%
MC: 39.2mb, 99.12%
v3-dp
思路
我们可以把方法转换为递归。
在上面的回溯中,最核心的一个步骤:
target -= num;
res += backtrack(candidates, target, cache);
在这里,我们可以将问题分解成更小的部分。
首先,我们必须创建一个大小等于 (target + 1) 的 Dp 数组,并将 0 索引初始化为 1。
dp[0] = 1;
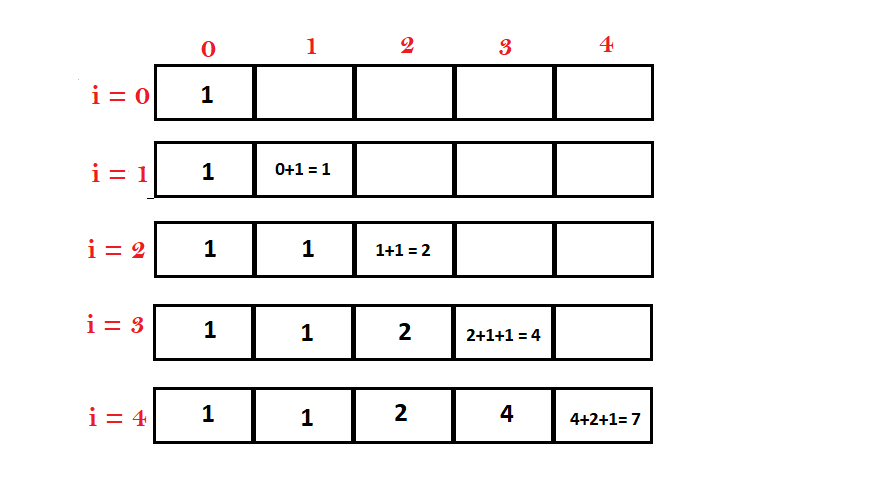
现在,我们将遍历数组并使用到达目标的方法数更新每个索引处的值。
其实我们可得到对应的递归公式。
java 实现
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target+1];
dp[0] = 1;
for(int i = 1; i <= target; i++) {
// 处理逻辑
for(int num : nums) {
if(num <= i) {
dp[i] += dp[i-num];
}
}
}
return dp[target];
}
效果
TC: 1ms, 83.1%
MC: 39.4mb, 92.67%
小结
希望本文对你有帮助,如果有其他想法的话,也可以评论区和大家分享哦。
各位极客的点赞收藏转发,是老马持续写作的最大动力!
开源地址
为了便于大家学习,所有实现均已开源。欢迎 fork + star~
参考资料
https://leetcode.cn/problems/combinations/
https://leetcode.cn/problems/combination-sum/
https://leetcode.cn/problems/combination-sum-ii/
https://leetcode.cn/problems/combination-sum-iii/
https://leetcode.com/problems/combination-sum-iv/
| [TLE to 100% beat | Optimisation | step by step | 7 solutions](https://leetcode.com/problems/combination-sum-iv/solutions/372950/tle-to-100-beat-optimisation-step-by-step-7-solutions/) |
https://leetcode.com/problems/combination-sum-iv/solutions/2381079/java-1ms-dp-top-down-memoization-easy/
