阮一峰老师的 6 大排序算法
互联网的出现,意味着”信息大爆炸”。
用户担心的,不再是信息太少,而是信息太多。
如何从大量信息之中,快速有效地找出最重要的内容,成了互联网的一大核心问题。
各种各样的排名算法,是目前过滤信息的主要手段之一。
对信息进行排名,意味着将信息按照重要性依次排列,并且及时进行更新。排列的依据,可以基于信息本身的特征,也可以基于用户的投票,即让用户决定,什么样的信息可以排在第一位。
下面,我将整理和分析一些基于用户投票的排名算法,打算分成六个部分连载,今天是第一篇。
基于用户投票的排名算法(一):Delicious和Hacker News
一、Delicious
最直觉、最简单的算法,莫过于按照单位时间内用户的投票数进行排名。
得票最多的项目,自然就排在第一位。
旧版的Delicious,有一个”热门书签排行榜”,就是这样统计出来的。
它按照”过去60分钟内被收藏的次数”进行排名。每过60分钟,就统计一次。
这个算法的优点是比较简单、容易部署、内容更新相当快;缺点是,一方面,排名变化不够平滑,前一个小时还排名靠前的内容,往往第二个小时就一落千丈,另一方面,缺乏自动淘汰旧项目的机制,某些热门内容可能会长期占据排行榜前列。
二、Hacker News
Hacker News是一个网络社区,可以张贴链接,或者讨论某个主题。
每个帖子前面有一个向上的三角形,如果你觉得这个内容很好,就点击一下,投上一票。
根据得票数,系统自动统计出热门文章排行榜。但是,并非得票最多的文章排在第一位,还要考虑时间因素,新文章应该比旧文章更容易得到好的排名。
Score = P-1 / (T+2)^G;
其中,
P表示帖子的得票数,减去1是为了忽略发帖人的投票。
T表示距离发帖的时间(单位为小时),加上2是为了防止最新的帖子导致分母过小(之所以选择2,可能是因为从原始文章出现在其他网站,到转贴至Hacker News,平均需要两个小时)。
G表示”重力因子”(gravityth power),即将帖子排名往下拉的力量,默认值为1.8,后文会详细讨论这个值。
从这个公式来看,决定帖子排名有三个因素:
(1)第一个因素是得票数P。
在其他条件不变的情况下,得票越多,排名越高。
从上图可以看到,有三个同时发表的帖子,得票分别为200票、60票和30票(减1后为199、59和29),分别以黄色、紫色和蓝色表示。在任一个时间点上,都是黄色曲线在最上方,蓝色曲线在最下方。
如果你不想让”高票帖子”与”低票帖子”的差距过大,可以在得票数上加一个小于1的指数,比如(P-1)^0.8。
(2)第二个因素是距离发帖的时间T。
在其他条件不变的情况下,越是新发表的帖子,排名越高。
或者说,一个帖子的排名,会随着时间不断下降。
从前一张图可以看到,经过24小时之后,所有帖子的得分基本上都小于1,这意味着它们都将跌到排行榜的末尾,保证了排名前列的都将是较新的内容。
(3)第三个因素是重力因子G。
它的数值大小决定了排名随时间下降的速度。
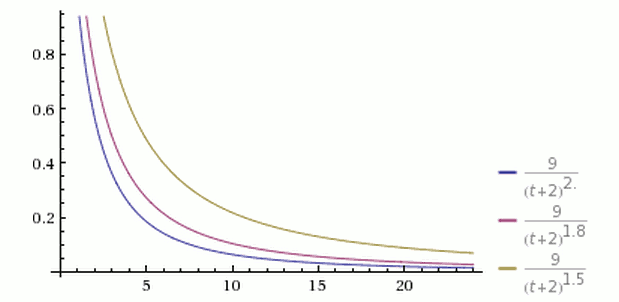
从上图可以看到,三根曲线的其他参数都一样,G的值分别为1.5、1.8和2.0。
G值越大,曲线越陡峭,排名下降得越快,意味着排行榜的更新速度越快。
知道了算法的构成,就可以调整参数的值,以适用你自己的应用程序。
基于用户投票的排名算法(二):Reddit
上一次,我介绍了Hacker News的排名算法。它的特点是用户只能投赞成票,但是很多网站还允许用户投反对票。
就是说,除了好评以外,你还可以给某篇文章差评。
Reddit是美国最大的网上社区,它的每个帖子前面都有向上和向下的箭头,分别表示”赞成”和”反对”。用户点击进行投票,Reddit根据投票结果,计算出最新的”热点文章排行榜”。
怎样才能将赞成票和反对票结合起来,计算出一段时间内最受欢迎的文章呢?如果文章A有100张赞成票、5张反对票,文章B有1000张赞成票、950张反对票,谁应该排在前面呢?
Reddit的程序是开源的,使用Python语言编写。
这段代码考虑了这样几个因素:
(1)帖子的新旧程度t
t = 发贴时间 - 2005年12月8日7:46:43
t的单位为秒,用unix时间戳计算。不难看出,一旦帖子发表,t就是固定值,不会随时间改变,而且帖子越新,t值越大。
至于2005年12月8日,应该是Reddit成立的时间。
(2)赞成票与反对票的差x
x = 赞成票 - 反对票
(3)投票方向 y
y是一个符号变量,表示对文章的总体看法。如果赞成票居多,y就是+1;如果反对票居多,y就是-1;如果赞成票和反对票相等,y就是0。
(4)帖子的受肯定(否定)的程度z
z表示赞成票与反对票之间差额的绝对值。如果对某个帖子的评价,越是一边倒,z就越大。如果赞成票等于反对票,z就等于1。
结合以上几个变量,Reddit的最终得分计算公式如下:
Score = log10 Z + yt / 45000
这个公式可以分成两个部分来讨论:
(一)
log10 Z
这个部分表示,赞成票与反对票的差额z越大,得分越高。
需要注意的是,这里用的是以10为底的对数,意味着z=10可以得到1分,z=100可以得到2分。也就是说,前10个投票人与后90个投票人(乃至再后面900个投票人)的权重是一样的,即如果一个帖子特别受到欢迎,那么越到后面投赞成票,对得分越不会产生影响。
当赞成票等于反对票,z=1,因此这个部分等于0,也就是不产生得分。
(二)yt / 45000
这个部分表示,t越大,得分越高,即新帖子的得分会高于老帖子。它起到自动将老帖子的排名往下拉的作用。
分母的45000秒,等于12.5个小时,也就是说,后一天的帖子会比前一天的帖子多得2分。结合前一部分,可以得到结论,如果前一天的帖子在第二天还想保持原先的排名,在这一天里面,它的z值必须增加100倍(净赞成票增加100倍)。
y的作用是产生加分或减分。当赞成票超过反对票时,这一部分为正,起到加分作用;当赞成票少于反对票时,这一部分为负,起到减分作用;当两者相等,这一部分为0。这就保证了得到大量净赞成票的文章,会排在前列;赞成票与反对票接近或相等的文章,会排在后面;得到净反对票的文章,会排在最后(因为得分是负值)。
(三)
这种算法的一个问题是,对于那些有争议的文章(赞成票和反对票非常接近),它们不可能排到前列。
假定同一时间有两个帖子发表,文章A有1张赞成票(发帖人投的)、0张反对票,文章B有1000张赞成票、1000张反对票,那么A的排名会高于B,这显然不合理。
结论就是,Reddit的排名,基本上由发帖时间决定,超级受欢迎的文章会排在最前面,一般性受欢迎的文章、有争议的文章都不会很靠前。
这决定了Reddit是一个符合大众口味的社区,不是一个很激进、可以展示少数派想法的地方。
基于用户投票的排名算法(三):Stack Overflow
上一篇文章,我介绍了Reddit的排名算法。
它的特点是,用户可以投赞成票,也可以投反对票。也就是说,除了时间因素以外,只要考虑两个变量就够了。
但是,还有一些特定用途的网站,必须考虑更多的因素。
世界排名第一的程序员问答社区Stack Overflow,就是这样一个网站。
排名算法的作用是,找出某段时间内的热点问题,即哪些问题最被关注、得到了最多的讨论。
在Stack Overflow的页面上,每个问题前面有三个数字,分别表示问题的得分、回答的数目和该问题的浏览次数。
以这些变量为基础,就可以设计算法了。
创始人之一的Jeff Atwood,曾经在几年前,公布过排名得分的计算公式。
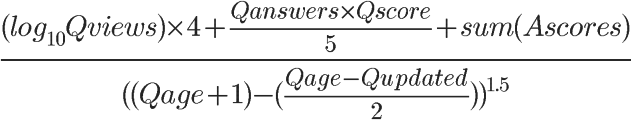
php 代码如下:
<?php
function hot($Qviews, $Qanswers, $Qscore, $Ascores, $date_ask, $date_active)
{
$Qage = (time() - strtotime(gmdate("Y-m-d H:i:s",strtotime($date_ask)))) / 3600;
$Qage = round($Qage, 1);
$Qupdated = (time() - strtotime(gmdate("Y-m-d H:i:s",strtotime($date_active)))) / 3600;
$Qupdated = round($Qupdated, 1);
$dividend = (log10($Qviews)*4) + (($Qanswers * $Qscore)/5) + $Ascores;
$divisor = pow((($Qage + 1) - ($Qage - $Qupdated)/2), 1.5);
echo $dividend/$divisor . "\n";
}
?>
各个算法变量的含义如下:
(1)Qviews(问题的浏览次数)
某个问题的浏览次数越多,就代表越受关注,得分也就越高。
这里使用了以10为底的对数,用意是当访问量越来越大,它对得分的影响将不断变小。
(2)Qscore(问题得分)和Qanswers(回答的数量)
首先,Qscore(问题得分)= 赞成票-反对票。
如果某个问题越受到好评,排名自然应该越靠前。
Qanswers表示回答的数量,代表有多少人参与这个问题。这个值越大,得分将成倍放大。这里需要注意的是,如果无人回答,Qanswers就等于0,这时Qscore再高也没用,意味着再好的问题,也必须有人回答,否则进不了热点问题排行榜。
(3)Ascores(回答得分)
一般来说,”回答”比”问题”更有意义。这一项的得分越高,就代表回答的质量越高。
但是我感觉,简单加总的设计还不够全面。这里有两个问题。
首先,一个正确的回答胜过一百个无用的回答,但是,简单加总会导致,1个得分为100的回答与100个得分为1的回答,总得分相同。
其次,由于得分会出现负值,因此那些特别差的回答,会拉低正确回答的得分。
(4)Qage(距离问题发表的时间)和Qupdated(距离最后一个回答的时间)
Qage和Qupdated的单位都是秒。如果一个问题的存在时间越久,或者距离上一次回答的时间越久,Qage和Qupdated的值就相应增大。
也就是说,随着时间流逝,这两个值都会越变越大,导致分母增大,因此总得分会越来越小。
(5)总结
Stack Overflow热点问题的排名,与参与度(Qviews和Qanswers)和质量(Qscore和Ascores)成正比,与时间(Qage和Qupdated)成反比。
基于用户投票的排名算法(四):牛顿冷却定律
这个系列的前三篇,介绍了Hacker News,Reddit和Stack Overflow的排名算法。
今天,讨论一个更一般的数学模型。
这个系列的每篇文章,都是可以分开读的。但是,为了保证所有人都在同一页上,我再说一下,到目前为止,我们用不同方法,企图解决的都是同一个问题:
根据用户的投票,决定最近一段时间内的”热文排名”。
你可能会觉得,这是一个全新的课题,伴随着互联网而产生,需要全新的方法来解决。但是,实际上不是。
我们可以把”热文排名”想象成一个”自然冷却”的过程:
(1)任一时刻,网站中所有的文章,都有一个"当前温度",温度最高的文章就排在第一位。
(2)如果一个用户对某篇文章投了赞成票,该文章的温度就上升一度。
(3)随着时间流逝,所有文章的温度都逐渐"冷却"。
这样假设的意义,在于我们可以照搬物理学的冷却定律,使用现成的公式,建立”温度”与”时间”之间的函数关系,轻松构建一个”指数式衰减”(Exponential decay)的过程。
伟大的物理学家牛顿,早在17世纪就提出了温度冷却的数学公式,被后人称作”牛顿冷却定律”(Newton’s Law of Cooling)。
我们就用这个定律构建排名算法。
“牛顿冷却定律”非常简单,用一句话就可以概况:
物体的冷却速度,与其当前温度与室温之间的温差成正比。
写成数学公式就是:
T'(t) = -α(T(t) - H)
其中:
-
T(t)是温度(T)的时间(t)函数。微积分知识告诉我们,温度变化(冷却)的速率就是温度函数的导数T’(t)。
-
H代表室温,T(t)-H就是当前温度与室温之间的温差。由于当前温度高于室温,所以这是一个正值。
-
常数α(α>0)表示室温与降温速率之间的比例关系。前面的负号表示降温。不同的物质有不同的α值。
这是一个微分方程,为了计算当前温度,需要求出T(t)的函数表达式。
第一步,改写方程,然后等式两边取积分。
假定室温H为0度,即所有物体最终都会”冷寂”,方程就可以简化为
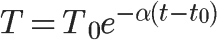
上面这个方程,就是我们想要的最终结果:
本期温度 = 上一期温度 x exp(-(冷却系数) x 间隔的小时数)
将这个公式用在”排名算法”,就相当于(假定本期没有增加净赞成票)
本期得分 = 上一期得分 x exp(-(冷却系数) x 间隔的小时数)
其中,”冷却系数”是一个你自己决定的值。如果假定一篇新文章的初始分数是100分,24小时之后”冷却”为1分,那么可以计算得到”冷却系数”约等于0.192。
如果你想放慢”热文排名”的更新率,”冷却系数”就取一个较小的值,否则就取一个较大的值。
ps: 如果只考虑冷却,显然也是不合理的,因为有的文章,热度会因为用户的参与反而上升
所以比较合理的是,有一个加热的过程,也有一个自然冷却的过程。
基于用户投票的排名算法(五):威尔逊区间
迄今为止,这个系列都在讨论,如何给出”某个时段”的排名,比如”过去24小时最热门的文章”。
但是,很多场合需要的是”所有时段”的排名,比如”最受用户好评的产品”。
这时,时间因素就不需要考虑了。
这个系列的最后两篇,就研究不考虑时间因素的情况下,如何给出排名。
一种常见的错误算法是:
得分 = 赞成票 - 反对票
假定有两个项目,项目A是60张赞成票,40张反对票,项目B是550张赞成票,450张反对票。
请问,谁应该排在前面?
按照上面的公式,B会排在前面,因为它的得分(550 - 450 = 100)高于A(60 - 40 = 20)。
但是实际上,B的好评率只有55%(550 / 1000),而A为60%(60 / 100),所以正确的结果应该是A排在前面。
Urban Dictionary就是这种错误算法的实例。
另一种常见的错误算法是
得分 = 赞成票 / 总票数
如果”总票数”很大,这种算法其实是对的。问题出在如果”总票数”很少,这时就会出错。
假定A有2张赞成票、0张反对票,B有100张赞成票、1张反对票。这种算法会使得A排在B前面。这显然错误。
Amazon就是这种错误算法的实例。
那么,正确的算法是什么呢?
我们先做如下设定:
(1)每个用户的投票都是独立事件。
(2)用户只有两个选择,要么投赞成票,要么投反对票。
(3)如果投票总人数为n,其中赞成票为k,那么赞成票的比例p就等于k/n。
如果你熟悉统计学,可能已经看出来了,这是一种统计分布,叫做”二项分布”(binomial distribution)。
这很重要,下面马上要用到。
我们的思路是,p越大,就代表这个项目的好评比例越高,越应该排在前面。但是,p的可信性,取决于有多少人投票,如果样本太小,p就不可信。好在我们已经知道,p是”二项分布”中某个事件的发生概率,因此我们可以计算出p的置信区间。所谓”置信区间”,就是说,以某个概率而言,p会落在的那个区间。比如,某个产品的好评率是80%,但是这个值不一定可信。根据统计学,我们只能说,有95%的把握可以断定,好评率在75%到85%之间,即置信区间是[75%, 85%]。
这样一来,排名算法就比较清晰了:
第一步,计算每个项目的"好评率"(即赞成票的比例)。
第二步,计算每个"好评率"的置信区间(以95%的概率)。
第三步,根据置信区间的下限值,进行排名。这个值越大,排名就越高。
这样做的原理是,置信区间的宽窄与样本的数量有关。比如,A有8张赞成票,2张反对票;B有80张赞成票,20张反对票。这两个项目的赞成票比例都是80%,但是B的置信区间(假定[75%, 85%])会比A的置信区间(假定[70%, 90%])窄得多,因此B的置信区间的下限值(75%)会比A(70%)大,所以B应该排在A前面。
置信区间的实质,就是进行可信度的修正,弥补样本量过小的影响。如果样本多,就说明比较可信,不需要很大的修正,所以置信区间会比较窄,下限值会比较大;如果样本少,就说明不一定可信,必须进行较大的修正,所以置信区间会比较宽,下限值会比较小。
二项分布的置信区间有多种计算公式,最常见的是”正态区间”(Normal approximation interval),教科书里几乎都是这种方法。
但是,它只适用于样本较多的情况(np > 5 且 n(1 − p) > 5),对于小样本,它的准确性很差。
1927年,美国数学家 Edwin Bidwell Wilson提出了一个修正公式,被称为”威尔逊区间”,很好地解决了小样本的准确性问题。
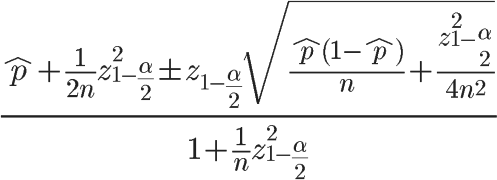
在上面的公式中,P’ 表示样本的”赞成票比例”,n表示样本的大小,z1- a/2 表示对应某个置信水平的z统计量,这是一个常数,可以通过查表或统计软件包得到。
一般情况下,在95%的置信水平下,z统计量的值为1.96。
基于用户投票的排名算法(六):贝叶斯平均
上一篇介绍了”威尔逊区间”,它解决了投票人数过少、导致结果不可信的问题。
举例来说,如果只有2个人投票,”威尔逊区间”的下限值会将赞成票的比例大幅拉低。
这样做固然保证了排名的可信性,但也带来了另一个问题:排行榜前列总是那些票数最多的项目,新项目或者冷门的项目,很难有出头机会,排名可能会长期靠后。
以IMDB为例,它是世界最大的电影数据库,观众可以对每部电影投票,最低为1分,最高为10分。
这里就有一个问题:热门电影与冷门电影的平均得分,是否真的可比?举例来说,一部好莱坞大片有10000个观众投票,一部小成本的文艺片只有100个观众投票。这两者的投票结果,怎么比较?如果使用”威尔逊区间”,后者的得分将被大幅拉低,这样处理是否公平,能不能反映它们真正的质量?
一个合理的思路是,如果要比较两部电影的好坏,至少应该请同样多的观众观看和评分。既然文艺片的观众人数偏少,那么应该设法为它增加一些观众。
在排名页面的底部,IMDB给出了它的计算方法。
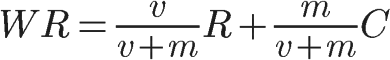
-
WR, 加权得分(weighted rating)。
-
R,该电影的用户投票的平均得分(Rating)。
-
v,该电影的投票人数(votes)。
-
m,排名前250名的电影的最低投票数(现在为3000)。
-
C, 所有电影的平均得分(现在为6.9)。
仔细研究这个公式,你会发现,IMDB为每部电影增加了3000张选票,并且这些选票的评分都为6.9。
这样做的原因是,假设所有电影都至少有3000张选票,那么就都具备了进入前250名的评选条件;然后假设这3000张选票的评分是所有电影的平均得分(即假设这部电影具有平均水准);最后,用现有的观众投票进行修正,长期来看,v/(v+m)这部分的权重将越来越大,得分将慢慢接近真实情况。
这样做拉近了不同电影之间投票人数的差异,使得投票人数较少的电影也有可能排名前列。
把这个公式写成更一般的形式:
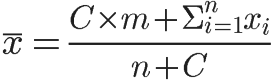
-
C,投票人数扩展的规模,是一个自行设定的常数,与整个网站的总体用户人数有关,可以等于每个项目的平均投票数。
-
n,该项目的现有投票人数。
-
x,该项目的每张选票的值。
-
m,总体平均分,即整个网站所有选票的算术平均值。
这种算法被称为”贝叶斯平均”(Bayesian average)。因为某种程度上,它借鉴了”贝叶斯推断”(Bayesian inference)的思想:既然不知道投票结果,那就先估计一个值,然后不断用新的信息修正,使得它越来越接近正确的值。
在这个公式中,m(总体平均分)是”先验概率”,每一次新的投票都是一个调整因子,使总体平均分不断向该项目的真实投票结果靠近。投票人数越多,该项目的”贝叶斯平均”就越接近算术平均,对排名的影响就越小。
因此,这种方法可以给一些投票人数较少的项目,以相对公平的排名。
=================================================
“贝叶斯平均”也有缺点,主要问题是它假设用户的投票是正态分布。比如,电影A有10个观众评分,5个为五星,5个为一星;电影B也有10个观众评分,都给了三星。
这两部电影的平均得分(无论是算术平均,还是贝叶斯平均)都是三星,但是电影A可能比电影B更值得看。
解决这个问题的思路是,假定每个用户的投票都是独立事件,每次投票只有n个选项可以选择,那么这就服从”多项分布”(Multinomial distribution),就可以结合贝叶斯定理,估计该分布的期望值。
由于这涉及复杂的统计学知识,这里就不深入了,感兴趣的朋友可以继续阅读William Morgan的How to rank products based on user input。
