第1章布尔逻辑 Boolean Logic
一些简单的事情,我们往往把它们搞得很复杂以至于几乎使我们失败。
—John Ashbery(1927),美图诗人
每种数字设各——比如个人电脑、手机或者网络路由器——都是基于一组用于储存利处理信息的芯片构建而成的。
虽然这些芯片在外形上、构成上不尽相同,但是它们都是由相同的构造模块制造而成的:基本的逻辑门(logicgates)。
这些逻辑门可能会由很多不同的原材料和制造工艺来文现,但是其逻辑行为在所有的计算机中都是一致的。
在本章中,我们从原始的逻辑门“与非门”出发,以此来构建其他逻辑门。
得到的是一组相当标准的逻辑门,这些逻辑门在后面将会被用来构建计算机的处理和存储芯片,具体内容分别会在第2章和第3章介绍。
从本章开始,本书中所有的硬件相关章节都具有相同的内容组织结构。
每一章都会集中讨论一个明确的设计任务——构建或整合某一组芯片。
每一章开头的背景知识部分都会对学握该设计任务所需要的预备知识作简要的背景介绍。
接下来的规范详述部分会对芯片的逻辑抽象作详述,即这些芯片通过某种方式所能实现的各种功能。
在了解了这些功能后,再接下来的实现部分将会对我们如何真正实现这些芯片提供思路和线索。
在观点这一节中,将对该章选漏的一些重要问题作总结。
每章的最后都有一个技术项目。
这一部分会给大家在个人计算机上实际构建芯片提供具体到每一操作步骤的指导,实验中將会用到随本书提供的硬件仿真器。
因为本章是全书第一个硬件章节,背景知识部分的介绍相对较长,在这一节里面特别介绍了硬件描述(hardare description)和仿真工具(simulation tools)
1.1 背景知识 Background
本节主要介绍一组简单的芯片即布尔门(Booleangate)的构建。
因为布尔门是对布尔函数(Boolean function)的物理实现,因此我们首先对布尔代数(Boolean algebra)作简单的介绍。
然后我们介绍如何将这些简单的布尔门相互连接来实现复杂芯片的功能。
本节的末尾介绍了如何在实际中使用软件仿真来进行硬件设计。
1.1.1 布尔代数 Boolean Algebra
布尔代数处理布尔型(也称为二进制型)数值,比较典型的有true/false、1/0、yes/no、on/off等等。
在这里我们使用1和0。
布尔型函数(Booleanfunction)是指输入输出数值均为布尔型数值的函数。
因为计算机硬件基于二进制数据的表示和处理,所以布尔函数在硬件体系结构的描述、构建和优化过程中粉演着十分重要的角色。
那么正确地表达和分析布尔函数是迈向构建计算机体系结构的第一步。
真值表表示法(Truth Table Representation) 描述布尔函数最简单的方法就是枚举出函数所有可能的输入变量组合,然后写出每一种组合所对应的两数输出值。
这就是真值表表示法,参看图1.1。
- 图 1.1 布尔函数真值标识
| x y z | f(x,y,z) |
|---|---|
| 0 0 0 | 0 |
| 0 0 1 | 0 |
| 0 1 0 | 1 |
| 0 1 1 | 0 |
| 1 0 0 | 1 |
| 1 0 1 | 0 |
| 1 1 0 | 1 |
| 1 1 1 | 0 |
图1.1中的前三列枚举出了函数变最所有的二进制值,有2^n个可能的元组w…v.(这里n=3),对于任何一个元组,最后一列给出对应的值f(v1…vn)
布尔表达式(Boolean Expressions)除了真值表描述之外,布尔两数还可以在输入变量上使用布尔算子(Boolean operator)来描述。
基本的布尔算子有“And”(只有在x和y都为1时,xAndy的值等于1),“Or”(x或者y中只要有一个为1时,xOry的值为1以及“Not”(当x为0时,Notx为1)。
我们将使用常用的计算符号来表示这些算子:x•y(或者xy)代表,Andy,x+y代表xOry,x^代表Not.x。
我们再来看看图1!,该真伯表可以用布尔表达式 f(x,y,z)=(x+y)•z^三来表示。
例如,当输入x=0,y=1,2=0(表中的第三行)时,x+y=1,因此1.0=1-1=1。
如果要完全验证布尔表达式和真值表的一致性,就取每一种可能的输入变最值的组合,看通过表达式计算出来的结果是否和表中最右列的值一致。
规范表示法(Canonical Representation)每个布尔兩数都至少由一个布尔表达式来描述,称之为规范表示法(canorical representation)。
同样从函数的真值表出发,我们关注两数值为1的那些行。
对于每一行,我们构建一种表达法米确定所有输入变量的值,即通过对两个字而量(literals)(每个量可以是变量本身或其反值)施以And操作来得到。
比如说图1.1中的第三行,函数的值为1。输入变量为x=0,y=1,2=0,于是我们构建表达式好y。
同样地,x文和1z分别代表第5行和第7行。
现在如果我们把这些表达式用Or操作联合起米(对于所有的西数值为1的行),那么可以得到跟给定的真值表一致的布尔表达式。
于是图1!中的布尔函数的规范表示法可以写成 (f(x,y,z) = x~ y z~ + x y~ z~ + xy z~
由这种表示法得出一个重要结论:每个布尔函数,不管有多复杂,都可以只使用三个布尔算子And、Or、Not来完全表达。
2-输入变量的布尔西数(Two-Input Boolean Functions) 图1.1揭示了n个二进制变量能够构成的布尔函数的数量为2”。
例如,图1.2中列出了2个输入变是所能构成的16个布尔两数。右边的四列枚举出所有可能的二进制值的组合,每个函数都有常规的名字来描述它维含的操作。
这里举了一些例子:名称叫Nor的两数实际上是Not-Or的简称:
先对x和y进行Or操作,然后取反。
Xor函数则是异或的简称,即当两个变量的值相异时则返回1,相同时返回0。
相反,Equivalence函数则是当变量取值相同时返回1,相异时返回0。
If-x-then-y函数(也称为x冫y,或者“ximpliesy”)是当*为0或当x和y都为1时返回1。
表中其他两数就不再一一说明了。
- 1.2 所有的2变量函数
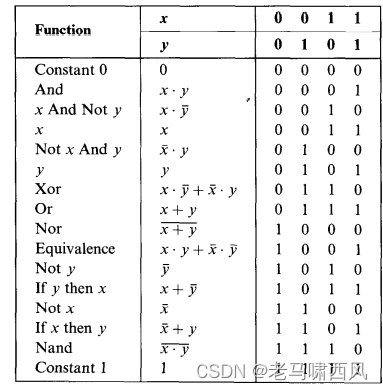
Nand函数以及Nor函数在理论上还有个有趣的特征:And/Or/Not算子都可以只用Nand或Nor函数来建构,(比如,xOry=(rNandx)Nand(yNandy))。
E既然每个布尔函数都能够通过规范表示法由And、Or和Not构成,那么每个布尔函数也能仅使用Nand函数来构成。
这个结论有比较深远的实际意义:一旦在物理上实现了Nand功能,就可以使用很多这样的物理设备,通过特定的连接方式来构建任何布尔函数的硬件实现。
1.1.2 门逻辑 Gate loogic
门(gate)是用来实现布尔两数的物理设备。
如果布尔函数子有n个输入变量,返回m个二进制的结果〈在我们前面所举的所有例子里面,m=1),那么用来实现这个兩数/的门将会有n个输入管脚(inputpins)和m个输出管脚(outputpins)。
当我们把一些值 v_1…v_n 从这些门的输入管脚输入,它的内部结构即门的逻辑会计算然后输出子(V…以)的值。
好比复杂的布尔两数能够通过相对简单的两数来表达一样,复茶的门电路也是由很多基本的门组成的。
最简单的门是由微小的开关设备(称为晶体管,transistors)构成,这些微小开关设备按照设计的拓扑结构进行连接,来实现整个门的功能。
蛋然当今的计算机多数使用电学来表达二进制数据从一个门到另一个门的传递,但实际上任何具有转换(switching)和传导(conducting)能力的技术都是可用的。
事实上,在过去的50年里,研究人员己经建立了很多布尔两数的硬件实现方法,包括磁、光、生物、水力和风力设备。
今天,大多数门都采用晶休管来实现,这些晶体管在硅上:蚀刻并封裝成芯片。
在本书里,我们所提到的芯片(chip)和门(gate)的概念是可交换使用的,但是门的概念一般用于描述简单的芯片。
有一点非常重要:一方面,我们有了多种可选的转换技术(switching technology),另一方面,我们又发现可以用布尔代数来对这些转换技术进行抽象。
简而言之这就意味者:计算机科学家们不必担心物理上的细节,比如电流、电路、开关、延迟和电源等等。
内部结构仅仅跟门电路设计者相关:而外部结构则是其他设计者所关心的问题一一他们希黑将门电路作为封装完好的抽象组件来使用,而不希望去考虑其内部结构。
因此,原始的门电路(primitivegate,如图1.3所示)能够被看成黑箱子,应用这些黑箱子来实现逻辑操作:
至于黑箱子内部的实现,我们并不关心。
硬件设计人员从这些基本的门开始,将它们进行连接,来实现功能更复杂的复合(compasite)门电路。

简单门和复合门(Primitive and CompositeGates) 所有的逻辑门都有相同输入和输出的语义表达(0和1),它们可以连起来构成具有任意复杂度的复合门电路(composite gates)。
例如,要实现一个具有三个输入变量的布尔函数And(a,b,e),可以通过使用布尔代数,按照 a•b•c=(a•b)•c或者前缀符号And(a,b,c)=And(And(a,b),c)来实现。
结果如图1.4所示。图1.4描述的是一个简单门逻辑(gatelogic)的例子,也称为逻辑设计(logicdesign有时候我们认为逻辑设计是一种连接门电路的艺术,目的是构建功能更复杂的门电路,即 复合门电路。
复合门电路本身就是某些布尔函数的实现,它们的“外部表现”(比如,图1.4中左边的图)跟基本门电路一致,虽然它们的内部结构可能会相当复杂。
对于任何给定的逻辑门,我们都能够从外部和内部两个不同方面对其进行观察。
图1.4中右边的图给出了门的内部结构(或称为内部实现),而左边的部分仅仅显示了门的外部接口(intercace),也就是输入和输出管脚。
内部结构仅仅与门电路的设计者相关,而外部结构则是其他设计者所关心的,他们仅使用门电路的抽象而不去关心其内部结构。
我们来看看另一个逻辑设计的例子:Xor门。
如前面所讨论的一样,当a和b的取值相异的时候,Xor(a,b)的值为1。那么我们可以用这个式子来表示:Xorla.b=Or(And(a,Not(b)),And(Nota).b)。
通过这个表示法,我们可以得到如图1.5所示的逻辑设计。
必须注意门的接口是唯一的:一般通过真值表、布尔表达式或者一些字面表述来实现。
- 图 1.5
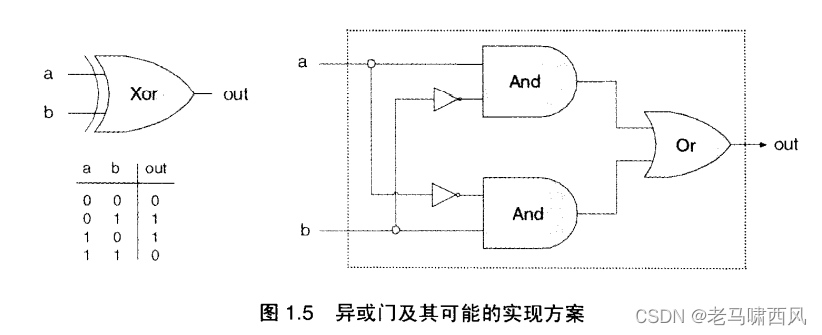
但我们能够使用很多不同的方法来实现这个接口,其中一些方法要在开销、速度和简洁程度等方面占有优势。
比如说,Xor函数可以使用4个And、Or、Not门]来实现,比5个门的实现方式要好。
虽然逻辑设计的基本功能可以通过这样或那样的方式实现其外部接口,但从效率的角度上来说,基本原则是用尽可能少的门来实现尽可能多的功能。
总的来说,可以这样描述選辑设计的艺术:给定门的描述(外部接口),通过应用已经实现的门,找到有效的方法来实现它。简单地说,这就是我们在本章后续内容中所要介绍的。
1.1.3实际硬件结构 Actual Hardware Construction
在介绍了由简单门电路组成复杂门结构的逻辑之后,现在该讨论这些门是如何来构建复杂结构的。我们首先从一个简单的例子来开始讨论吧。
假设我们在自家的车库开了一家芯片加工店。第一个定单是制造一百个Xor门。
我们用订单的订金去买了一支焊枪,一卷铜芯线和兰只分别貼有“And门”、“Or门”、“Not门”标签的箱子,每箱包含很多同类的基本门电路。
每个门电路都像电源插头那样用塑料盒子封裝起米,只有一些输入和输出管脚露在外面。
开始工作之前,把图1.5钉在车库的墙上。
首先,拿出两个And门,两个Not门和一个Or门,按照图中的布局把它们安裝在电路板上。
然后,用铜线把这些门一一连接起来,用焊枪把线和各自的输入/输出管脚焊超来。
如果我们仔细地按照图中所描述的电路进行连接,最后会留三个露在外面的线头,然后把线头和对应的三个管脚焊起来,把整个电路(除了三个管脚)封裝在一个塑料盒子里,然后 打上“Xor”的标记。制造好一个门之后,接下来就是重复地做上述工作。
一天下来,我们把制造好的所有的芯片裝在一只新的箱子里面,然后标上“Xor门”。
如果我们(或者其他人)以后要制造其他的芯片,可以使用这些Xor门作为基本的模块,就像我们以前使用And门、Or门、Not门一样。
读者们可能感到:在车库进行芯片制造会不会太落后,应该还有很多可以改进之处吧。
也许给定的芯片图纸不能保证其正确性。虽然我们能够证明一些简单芯片(比如Xor门)的正确性,但是对于许多复杂的芯片来说我们就无能为力了。
因此,我们必须进行经验性的测试:把芯片通上电源,分别给输入管脚注入高电平、低电平,通过不同的组合来验证芯片的输入是否和其描述一致。
如果芯片的输出不是所期望的值,就得修正它的物理结构,这是一件相当麻烦的事情。即使我们验证出电路的设计是完全正确的,重复的芯片制造过程将会是耗时、容易产生错误的事情。
一定有更好的办法吧
1.1.4 硬件描述语言(HDL) Hardware Deseription Langunge(HDL)
今天,硬件设计者再也不会用他们的那双手来制造硬件了。
取而代之的是,他们在计算机工作站上设计和优化芯片结构,使用结构化的建模形式比如硬件描述语言(Harduare Deseription Language),或HDL(大家都知道VHDL,其中V代表Virtual即處拟的)。
设计者通过编写HDL程序来描述芯片的结构,该程序将接受严格的测试。
该测试是虚拟的,使用计算机进行仿真的庭拟测试:有个特殊的软件工具称为硬件仿真器(hardoare simulator),它接受输入的HDL程序,在计算机内存中构建该虚拟芯片的内存映像。
然后,设计者就可以让仿真器来测试芯片,通过输入变最的不同组合产生仿真的芯片的输出。
将这些仿真的输出结果与预期的值进行比较,来验证我们的设计是否正确,是否满足客户的要求。
除了测试芯片的正确性之外,硬件设计者可能还比较关心一系列参数,比如计算速度、功粍和心片设计的,总成本等等。
所有这些參数也可以利用硬件仿真器来仿真和量化,帮助设计者对设计进行优化直到仿真的芯片达到期望的性价比。
因此,在投资进行实际的芯片生产之前,可以用HDL对整个芯片进行全面的设计、调试、优化。
当HDL程序完成之后,或者说,当仿真后的芯片性能满足客户的要求之后,HDL程序才能被作为在硅上蚀刻芯片的设计图。
芯片制造流程中的最后一步,即从优化的HDL程到大量生产,是典型的外包过程(交给专注于花片制造的公司来做),这其中要使用某种转换技术(switching tecbnology)
例子:构建Xor门门正如在图1.2和图1.5中看到的,描述异或逻辑的方式之一可以是 Xor(a,b)=Or(And(a,Not(b),And(Not(a),b))。
该選辑同样可以用图形(如门结构图或文字,或HDL程序)来表达。
Xor的HDL表达法请参看图1.6,关于HDL的介绍请参解释芯片的HDL定义包括header部分和parts部分。
Header部分描达了芯片的接口(interface),也就是心片的名称、输入输出管脚的名称。
parls部分描述了所有底层电路的名称和拓扑结构,这些电路是构成该芯片的基本部分。每个部分用一个statement(语句)来表示,它描述了该部分的名称以及与其他部分的连接方式。
为了简单明了地编与这些语句,HDL程序员必须有内在模块的接口文档。
例如,图1.6中假定了Nor门的输入输出管脚为in利out,And门和Or门的输入输出管脚分別为a,b和out。
- 图 1.6
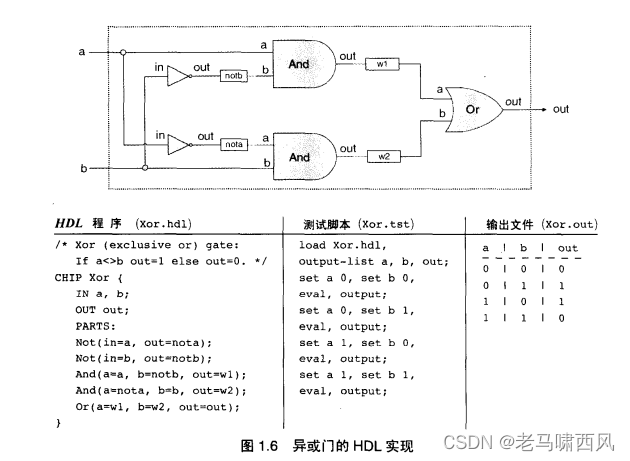
这种类似API的信息并不会显式给出,但是将parts部分插入HDL代码之前,必须保证能够对这些信息进行访间才行。
内部模块的连接是通过建立和连接内部管脚(internal pins)来描述的。
比如,图中Not门的输出管脚又和And门的输入管脚相连。
HDL代码通过 Not(...out=nota) 和 And(a=nota,...)米描述这个连接。
第一条语句建立了一个名为nota的内部管脚,并作为Not门的输出。第二条语句又将nota作为And门的输入管脚。注意到管脚可能有无限的扇出(fanout)。
比如,在图1.6中,每个输入都同时被作为两个门的输入管脚。在门结构的图中,我们使用节点(forks)来表示多重连接。
在HDL中,代码隐含了节点的存在。测试严格的质量认证要求设计出来的芯片必须在一种明确的、可重复和可读性强的方式下进行测试。
应用这种思想,硬件仿真器通常被设计用来运行用脚本语言(scripting language)编写的测试脚本(textscript)。
例如,图1.6中的用脚本语言编写的测试脚本能够被硬件仿真器读懂。关于脚本语言的介绍请参看附录B。
我们来对图1.6中介绍的测试脚本作简单地解释。测试脚本的前两行指示仿真器加载Xor.hd1文件并准各输出所选择的变最。
接着,脚本列出了一系列的测试场景(testing scenarios),用来模拟Xor芯片在真实环境中可能产生的各种结果。
在每个测试场景中,脚本指示仿真器为芯片威予确定的输入值,计算出对应的测试结果,然后将该结果记录到指定的输出文件中。
对于一些简单的门(比如Xor),可以用穷尽法编写完整的测试脚本来罗列出選辑门电路所有可能的输入组合。
输出文件(图1.6的右边)可以看作是凭经验得出的芯片的正确输出结果。
然而,对于比较复杂的心片,这种经验性的验证就不适用了,我们在后面也会看到这一点。
1.1.5 硬件仿真 HardwareSimulation
HDL是一种结构化的硬件语言(hardware construction larguage),编写和调试HDL程序的过程跟软件开发相似。
它同软件开发的主要区别是,它应用硬件仿真器,而不是在HDL中用Java语言编写代码或用编译器编译测试代码。
硬件份真器其实是个计算机程序,它知道您样分析和解释HDL代码并且把它转换成可执行的表达式,然后根据给定的测试脚本来对代码进行测试。
在市面上有很多商用硬件仿真器,它们在价格、复杂度和使用方便程度上各不相同。
本书配套网站提供了一个简单的(free)硬件仿真器,对于一些成熟的硬件设计项目来说它是足够了。
该仿真器提供了木书中所沙及的芯片设计、测试和集成过程中所需的全部工具,以此来构建通用的计算机系统。
图1.7显示了一个典型的芯片仿真过程。
1.2 规范详述 Specification
这个部分详细介绍了一组典型的门电路,每个门被设计来执行-个常见的布尔操作。
这些门将在接下来的一些章节里面被用到。我们从原始的Nand门出发,其他的门电路能够通过这个门电路构建得到。
这县我们只提供门的说明或者接口,把具体的实现细节留在后续的章节中去介绍。
读者如果有兴趣自己通过HDL.来构建特定的门电路,可以参考附录A。
所有的门电路都能够在个人计算机上通过与木书配套的硬件仿真器来进行构建和仿真。
1.2.1 Nand门 The Nand Gate
我们对计算机结构的讨论从简单的Nand门开始,所有其他的门电路和芯片能够通过它来构建。
Nand门用于实现以下布尔函数:
| a b | Nand(a,b) |
|---|---|
| 0 0 | 1 |
| 0 1 | 1 |
| 1 0 | 1 |
| 1 1 | 1 |
纵观全书,我们使用“装箱的芯片API”来描述芯片。
对每个芯片,API描述了芯片的名字、输入输出管脚的名字、芯片所能执行的功能或操作以及必要的说明。
芯片名: Nand
输入: a, b
输出: out
功能: If a=b=1 then out=0 else out=1
说明: 此门是最基本的单元,不常要实现。
1.2.2 基本逻辑门 Basic Logic Gates
这里提到的逻辑门都是“基本的”门电路。
其中,每个门电路可仅由Nand门来组合构成。
因此,它们不应该被看作是“原始”的门。
Not单输入变最的Not门,也被称为“反相器(converter)”,将 0 反相为1输出或者将1反相为0输出。
它的API如下:
芯片名: Not
输入: in
输出: out
功能: if in=0 the nout=1 else out=0.
And
只有当输入都是1时,And函数输出1,否则就输出0。
芯片名: And
输入:a,b
输出:out
功能:If a=b=1, then out=l else out=0.
Or
只要输入变量中有1,Or函数就输出1,否则输出0。
芯片名: Or
输入:a,b
输出:out
功能:If a=b=0, then out=0 else out=1.
Xor
又称为“异或”,当两个输入值相反的时候,Xor函数输出1,其他情况返回0。
芯片名: Xor
输入:a,b
输出:out
功能:If a=/b, then out=1 else out=0.
Multiplexor
Multiplexor(见图1.8)是三输入变最的门电路,其中一个输入称为“选择位(Selection-bit)”,选择另外两个输入变量(称为数据位,databits〉中的一个作为输 出,另外两个输入称为“数据位”。
因此,这个门电路还有另一个比较好的名学:“选择器(selector)”。
Multiplexor这个名词来自于通信系统,意思是将多个相同设备的输出信号通过单一输出信号线串行地输出。
芯片名: Mux
输入:a,b, sel
输出:out
功能:If sel=0, then out=a else out=b.
Demultiplexor
Demultiplexor(见图1.9)执行与multiplexor相反的功能:它只有一个输入变量,然后根据一个选择位来决定到底从哪一个通道输出。
- 图 1.9
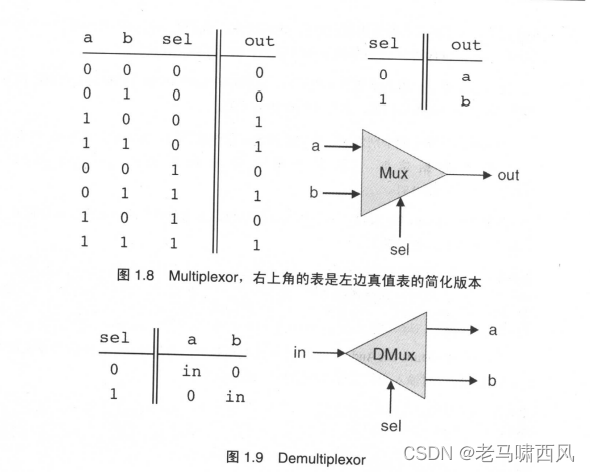
芯片名: DMux
输入:in, sel
输出:a,b
功能:If sel=0, then (a=in, b=0) else (a=0, b=in).
1.2.3 多位基本门 Multi-Bit Versions of Basic Gates
通用计算机的设计要求其能够在多位数据线(又称为“总线”,bus)上运行。
比如,32位计算机的基本要求是能够在2个给定的32位总线上按位(bit-wise)进行And函数的计算,我们可以构建一个32位And门阵列,每个And门能够独立地处理一对输入变量的
And运算。为了把所有的逻辑封裝在同一个包里面,我们把这些门阵列压缩在一个单一的芯片接口里,包含两个32位的输入总线和一个32位的输出总线。
这一节介绍了一组典型的多位逻辑门,这些门在构建16位计算机时会用到。
同n位逻辑门的结构是基本相同的,并与n的具体值无关。
当涉及到总线上的个别位时,我们通常使用数组的语法。
比如说,在描述16位.总线data的各数据位时,我们使用这样的表达法:data[0], data[1], …., data[15]
多位 Not(Multi-BitNot)
n位的Not门所执行的布尔操作是:对它的n位输入总线上的每一位取反,然后输出。
芯片名:Not16
输入:in[16] //16-bit管脚
输出:out[16]
功能: For i=0..15 out[i] = Not(in[i])
多位And(Multi-BitAnd)
n位的And门所执行的布尔操作是:对两个n位输入总线上对应的每一对输入变量进行“与操作”,然后输出。
芯片名:And16
输入:a[16], b[16]
输出:out[16]
功能: For i=0..15 out[i] = And(a[i], b[i])
多位Or(Multi-BitOr)
n位的Or门所执行的布尔操作是:对两个n位输入总线上对应的每一对输入变量进行“或操作”,然后输出。
芯片名:Or16
输入:a[16], b[16]
输出:out[16]
功能: For i=0..15 out[i] = Or(a[i], b[i])
多位Multiplexor(Muli-BitMultiplexor)
n位multiplexor的结构跟图1.8中所描述的二进制multiplexor几乎完全一样,只是原来两个1bit位的输入变量都变成了两个n位的输入变最:选择位仍然是1,
芯片名:Mux16
输入:a[16], b[16], sel
输出: out[16]
功能: If sel=0 then for i=0..15 out[i]=a[i] else for i=0..15 out[i]=b[i]
1.2.4 多通道逻辑门 Multi-Way Versions of Basic Gates
很多2位(即接收两个输入)的逻辑门能够推广到多位(即接收任意数量的输入这一节介绍一组多位门电路,它们将在以后介绍的计算机体系结构中的各种芯片中使用。
相同的推广方式可以应用到其他的体系结构中。
多通道Or(Muli-WayOr)
对于一个n位的Or门,当n位输入变量中任意一位或一位以上为1,输出就为1,否则就为0。这里给出8位的例子。
芯片名: Or8Way
输入: in[8]
输出:out
功能:out = Or(in[0], in[1], ...., in[7])
多通道/多位Multiplexor(Multi-Way/Multi-BitMultiplexor)
一个拥有m个通道、每个通道数据宽度为n位的multiplexor选择器,将m个n位输入变量中选择一个并从其单一的n位输出总线上输出。
我们用k个控制位来指定这个选择,这里k=log3m。图1.10描述了一个典型的例子。
- 图 1.10
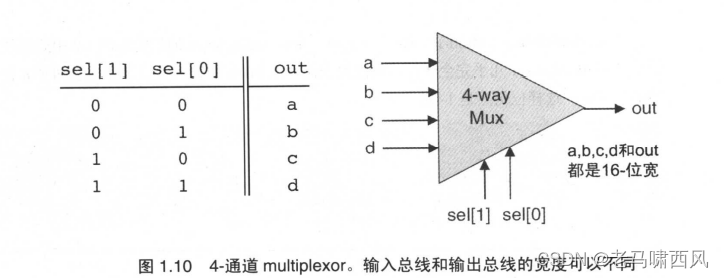
下面给出了两个API的例子:一个4通道16位的mutiplexor和一个8通道16位的multiplexor。
芯片名: Mux4Way16
输入:a[16], b[16], c[16], d[16], sel[2]
输出:out[16]
功能: sel=00=>a; sel=01=>b; sel=10=>c; sel=11=>d
说明:上迷默值操作都是16-位操作。比如,"out=a,意指for i=0..15 out[i]=a[i]
芯片名: Mux8Way16
输入:a[16], b[16], c[16], d[16], e[16],f[16],g[16],h[16],sel[3]
输出:out[16]
功能: sel=000=>a; sel=001=>b; ... sel=111=>h
说明:上迷默值操作都是16-位操作。比如,"out=a,意指for i=0..15 out[i]=a[i]
多通道/多位Demultiplexor(Multi-Way/Multi-BitDemultiplexor)
m通道、n位的demultiplexor(见阁1.11)从m个可能的n位输出通道中选择输出一个n位的输入变量。
- 图 1.11

我们用人个控制位来指定这个选择,这里k=log3m。
下面给出了两个API的例子:一个4通道1位的demultiplexor和一个8通道1位的 demultiplexor。
芯片名: DMux4Way
输入:in, sel[2]
输出:a,b,c,d
功能: if sel=00 then {a=in, b=c=d=0}; else if sel=01 then {b=in, a=c=d=0}; else if sel=10 then {c=in, a=b=d=0}; else if sel=11 then {d=in, a=b=c=0}
芯片名: DMux8Way
输入:in, sel[3]
输出:a,b,c,d,e,f,g,h
功能: if sel=000 then {a=in, b,c,d,e,f,g,h=0}; .... else if sel=111 then {h=in, a,b,c,d,e,f,g=0}
1.3 实现 Implementation
跟数学中公理的的丝一样,原始门电路提供了一系列的基本模块,其他的门电路可以通过这步楼块来构建。
原始门是成熟的商用组件,因此可以波用来构建其他门电路和芯片。
而不用去担心它们的内部结构。在我们开始构建计算机体系结构的起炒阶段。
仅仅只使用原始门Nand米构建所有便件。我们現在开始勾勒这个自底向上的硬件构建项目中的第一步,每次实现一个门。
我们意只部分实现门电路,目的是让设者自己开发门中路的体系结构。这里再次重中:每个门电路都能菇采用不止一种方式来实现:超简单的实现方法糖好。
Not:应用一个2位Nand门来实现一个1位Nox门是很容易的。小捉示:请大家考惠正向思维。
And:最Nort门一样,其实现也是很客易的。
Or/Xor:这热西数能修機蛋前而所实现的布尔函數来定义,使用一此简单的布尔樂
Multipleoxr/Demultiplexor:同祥,这装门依华使用前面己经构建好的门电路来实现。
多位NotAnd/or门(Mulei-BitNouAnd/OrGates),既然我们己经知道了如何来实现基本的NouAndor门],那么对月位门的实现就是将n个基本门组成阼列的过程,饼个 门独立地处理各自对应的位。这项正作可能有点繁琐,但是当这些多位门成用在复梨芯片上时,这项工作就湿得很重娶了,这一点將会在層面的豪节具休介绍。
多位Multiplexor(Multi-BitMultiplexor):n位的multiplexor的实现是简单地将相同的选择位感予片个二元multiplexor。这个繁琐的工作同样可以构建非常有用的芯片, 多位门(Multi-WayGates):实现小提示:想家一下吃饭的叉子。
1.4 观点 Perspective
本章介绍了应用数字设计项目中的第一步,在下一章会使用本章所实现的门电路米构建更复杂的功能模块。
尽管我们选祥Nand门作为基本构建模块,实际上其他的一些方法也足可行的。
例如,可以只使用Nor门来构建完整的计算机平台,或者综合使用And门、or门和Not门。这些選辑设计的方法从理论上来说是相同的,就像几何学里面所有的理论都可以由一些持相反观点的公理来建立一样。关于理论和实际构建方法可以参看数字设计(digitaldesign)和選辑设计(logicdesign)相关的教材。
纵观本章,我们并没有去考忠设计的效率问题,比如在构建复合门电路时,设计中沙及到所使用的基本门的数爸或者交叉线路的数量。
这些问题在实际的设计生产中是极其重要的,大最的计算机专家和电子工程师们都在研究如何优化它们。
另外一个根本没有提到的问题是门电路和芯片具体的物理实现,比如嵌入到硅上面的晶体管。当然有很多实现方式上的选择,每种方式都有它自己的特点(速度、供电、生产成本等等)。要了解这些问 题需耍电子学和物理学上的背最。
1.5 项目 Projeet
目标实现本章提到的所有選辦门。
你能使用的构建楼块只能是原始的Nund门以及由此所构建的一些复合门。
资源这个项目里你所需要的唯一工具是与本书配套的硬件仿真器。所有的芯片应该利用HDL语言(参看附录A)来描述。
对于本章中提到的每种芯片,我们都提供了只有框架没有具体细节实现的.idn骨下程摩(文本文件)。
另外,我们还提供了.tst脚本文件,用来告诉硬件仿真器如何进行测试,同时開本文件将会产生一个正确的.cmp输出文件或称“比较文件(comparefile)”,你委做的就是完成空缺.ha1程序里面的具体文现部分。
约定当你设计的芯片〈用.ha2程序表示)被加我到硬件仿真器中,并利用.tet文件进行测试后,应该在.cmp文件中生成锦出列表。若结果不如所料,仿真器会给出相应 的提示。
TBC
P46…
参考资料
《从零开始构建现代计算机》
