创作原因
不久前,我发现需要一台PNG装载机用于我的一个小项目。作为一个完整的工具,我当然决定自己写一个 - 毕竟,为什么在还有车轮等待重新发明时为自己省力?如果你愿意的话,可以在这里查看inflater代码的来源 - 它写得非常干净。事实上,我专门写它是为了易于阅读,而不是最快的实现。
我当时对Deflate了解不多。我知道它基于LZ系列算法(LZ77 / L7SS等)。我听说有人说它只是“只是”LZSS,除了他们在匹配向量上应用霍夫曼编码。嗯,事实证明这是真的。均田。但是当我更深入地阅读规范时,它让我觉得这里发生了一些非常聪明的事情,我之前没有看到过任何明确提出过的事情。所以我想为什么不试着在这里解释Deflate的本质。我不打算在严格的细节上涵盖整个工作;如果你想要那就去阅读规范。
Deflate是由Phil Katz于1993年发明的,它构成了ZIP文件格式,zlib库,gzip,PNG以及其他一些东西的基础。当时它非常前沿。当时的主要竞争对手通常是LZW,或者也许是LZSS。在许多人的眼中,压缩仍然是游程编码的同义词,因此当Deflate出现时它肯定会变成一些头脑。现在这已经超过了20年,所以后来像LZMA这样的编解码器(我可能有一天会写一下)可以定期击败它。它仍然没有死。
勘误表
因此,LHA归档程序也使用了此处描述的基本原理,它早于PKZIP 2.0。也许我可以说这篇文章是“LHA的优雅”?好吧,我不会,所以那里。历史是由胜利者和具有更好的首字母缩略词的人写的。
压缩
压缩有两种基本方法。好吧不,那不是真的,但不管怎样,让我们继续吧,然后按下。
老实说,如果你对压缩有所了解,你很可能会对此大部分都有所了解,但这里无论如何。
-
基于熵的压缩
-
基于字典的压缩
基于熵的压缩是一个非常古老的想法。计算机通常将字母存储为8位;每个字母一个字节。
“多么浪费,”有人想。像E和T这样的字母很常见,而像Q和Z这样的字母很少出现。有意义的是,你想要更少的位用于更常见的字母。
独立宣言的频率计数。小写占主导地位,资本几乎不存在。
这个想法甚至早于计算机。去看摩尔斯代码 - 英语中最常见的两个字母(E和T)只是一个点和短划线。
霍夫曼编码是一种非常古老而简单的应用方法。您从“字母表”开始 - 您要编码的所有符号的集合。在学校的英语,我们被告知我们的字母表是26个字母。然而,在计算机中,我们还需要更多。我们需要存储大写字母,小写字母,数字,标点符号,我们需要一个“空间”符号和一些其他小东西。获得完整的字母后,您需要分配概率。我们知道一些字母(e / t / a / i / etc)比其他字母(q / x / y / z / etc)更常见,但我们还必须考虑这个扩展字母表的其余部分。数字在英国散文中很少见,首都也是如此。本段有五百六十一个小写字母,但只有十个大写字母。
一旦你的概率全部整理出来,你就构建了一个霍夫曼树。这为每个字母分配了一个唯一的代码,除了“自我终止”的方式。即,您不需要存储任何其他信息来说明每个字母的开始和停止位置。如果你看一下摩尔斯电码的例子,就不会那样。虽然莫尔斯有点和短划线,但它也有间隙,需要间隙来分割字母。霍夫曼编码不需要间隙。
所以这是熵编码 - 你决定使用字母表,你使用较少的位来存储常见的东西,使用更多的位来处理稀有事物。你可以用它来压缩像英语这样的东西,虽然它工作得很好,但它还有很大的改进空间。当然,这是比霍夫曼编码更好的方法,比如算术编码,但霍夫曼是最容易理解的。这也是Deflate使用的东西,所以我们会把它留在那里。
LZ77
LZ77构成了基于字典的算法的基础。字典压缩的想法很简单,某些事情在文档中出现不止一次。
例如,如果您在此页面中搜索“压缩”一词,则会多次出现。因此,不要每次都再次存储它,让我们尝试参考之前的用法。
LZ77非常简单。您存储匹配向量(由长度和距离组成的一对),并在匹配后存储结束匹配的字母(“文字”)。
因此,例如,如果我想存储短语sense和sensibility,我们会看到sens部分被使用了两次。所以我们可能会将第二种用法存储为返回10,复制4,字母i,因为我们需要复制“sens”的4个字母,然后在最后添加新的i。
看起来很好,对吗?不,LZ77很糟糕。虽然它可以通过参考之前的短语来节省空间,但这就是它所能做到的。模式是固定的 - 它存储了一个匹配,然后是一个字母。但如果 没有匹配怎么办?要使用相同的示例,以下是LZ77实际存储整个报价的方式:
输入:感觉和感性
输出:[返回0,复制0] s [返回0,复制0] e [返回0,复制0] n [返回0,复制0] s [返回0,复制0] e [返回0,复制0] [返回0,复制0] a [返回0,复制0] n [返回0,复制0] d ...
真是一团糟。你明白了。它必须存储一个匹配,即使没有匹配。并且存储该空匹配信息需要空间。典型的矢量可能是16位(距离返回为12位,长度为4位)。所以以前每个字母8位的东西现在最终可以达到每个字母24位!这就是没有人使用原始LZ77的原因。
因此他们发明了LZSS,这是许多早期档案馆使用的。 LZSS存储一个比特来说明下一个出现的是匹配向量还是文字符号。这是一个非常明显的想法,我不知道为什么不早点想到它。所以现在我们的额外标记位允许我们标记匹配向量是否为空,并简单地跳过所有浪费的开销。
无论如何,这是字典压缩。当它能够获得很多好的比赛时,它的效果非常好。不过,这是多余的一点。我们用来表示我们是否匹配的那个讨厌的“文字”位。如果没有匹配会怎么样?在那种情况下,我们已经从最初每个字母存储8位到存储9位!如果没有匹配发生,LZSS将存储1位以指示字母,然后再存储8位以存储该字母!
LZ77,LZSS和家族中的其他人都遭遇同样的问题,不得不切换模式的开销 - 当他们发现不适合基于字典的匹配类的东西时,他们需要写出某种类型的标记切换到文字模式。这一切都占用了流中的宝贵空间。 (如果你不小心,有时你会浪费这么多开头做这种切换,你实际上根本不压缩文件,你会放大它!)
所以我们有两种压缩算法。 LZSS依赖于找到以前匹配的数据,而Huffman编码依赖于某些字母比其他字母更常见。我们能比选择其中一个更好吗?我们可以把它们编织在一起吗?
我们可以。
Deflate
如果我们想要将这两种算法结合在一起,那么想象我们如何做到这一点并不是一个很大的飞跃。我们从LZSS开始吧?匹配部分似乎没问题,只是文字会让我们陷入困境,因为它们完全没有压缩。那怎么样 - 我们可以只用霍夫曼编码呢?我们存储一点,如果它是匹配或文字,如果它是匹配,那么我们写一个16位匹配向量,如果它是一个文字,那么我们写一个可变长度的霍夫曼编码符号。
我觉得这样做很好,但这并不是Deflate如何做到的。放气比这更进一步。您仍然需要支付该标记位的成本来切换模式。为了理解Deflate,我们需要扩展我们对字母表的概念。
你看,当我们听到“字母表”这个词时,我们回想起我们学到的孩子–A,B,C等等。但是当我们开始参与压缩时,我们知道事实并非如此。我们已经不得不扩展我们的字母表以包括大写字母和数字等。即使是甚至不可见的空间,我们也必须对它们进行编码。 Deflate只是将这个概念向前推进了一步。
Deflate基于统一字母表的概念。如果字母表只是一组选择,为什么不把所有选择放在一个伞下呢? Deflate的字母表由286个符号组成。前256个是每个字母的ASCII码,包括所有ASCII控制码和其他类似的ASCII码。其余30个符号用于表示长度。没错,我们在这里存储实际的匹配长度。这是使用的实际表格:
0-255 Regular input byte
256 End of data block
257 Match of length 3 (distance follows after)
258 Match of length 4 (distance follows after)
259 Match of length 5 (distance follows after)
260 Match of length 6 (distance follows after)
261 Match of length 7 (distance follows after)
262 Match of length 8 (distance follows after)
263 Match of length 9 (distance follows after)
... etc
除此之外还有更多内容,为了清楚起见,我在这里省略了,但希望这可以解释原理。 我们现在有286个符号,每个符号都有自己的概率,因此也有自己的霍夫曼代码。 我们知道有些字母仍然会更常见(E,T等)。 但比赛怎么样? 他们有多常见?
还记得我们之前如何获得英文文本的频率图吗? 那么这就是我们扩展字母表的外观:
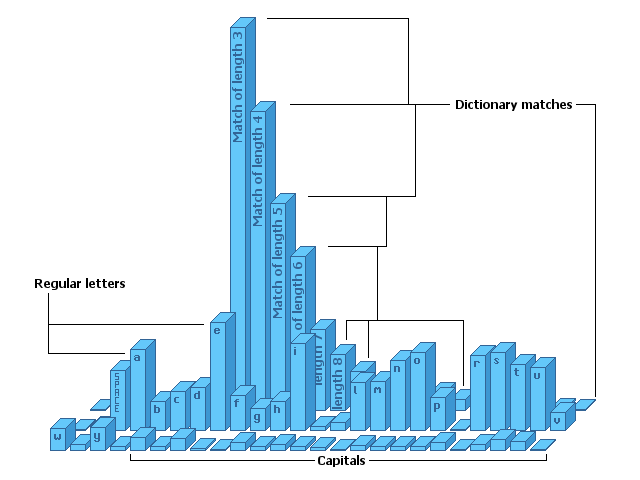
您可以看到小写的“e”很受欢迎,其他一些小写的“e”也很流行,比如“a / i / t / etc”。
资本几乎不存在,在这种情况下根本没有数字。然而有些东西像拇指一样伸出 - 字典匹配主导概率域。同样有趣的是,小写字母的概率已经改变,因为字典匹配晚上它。
当我们一次压缩一个符号的数据时,我们在每个压缩阶段都会面临一个选择。如果我们可以找到前一个匹配,那么我们可以将该匹配向量写出来,如果我们不这样做,那么我们就写出文字符号。但是Deflate的独特之处在于它与前辈的区别在于,无论我们选择何种选项,我们都只会写出一个单独的霍夫曼编码符号。
如果我们想要连续存储两个匹配项,或者连续存储两个文字,我们可以这样做。一个字母表存储两个不同的想法。指定模式之间切换不需要位标记。我们存储根据频率压缩的文字字母,我们也根据它们的频率存储匹配长度,但不止于我们在一个统一的方案下做这两件事。
它不是一种算法而是两种算法,它们和谐共舞。您可以选择字典匹配或熵编码,您可以在每个字节的基础上选择它们,而无需开销。这就是我发现它如此聪明 - 不是它可以做一件事或另一件事,而是它可以选择任何一种,但用同一种语言代表它们。没有额外的标记,没什么可说的“哦,现在我们正在切换到熵模式”,没有什么可以阻碍。
它是一个RLE编码器,它是一个字典匹配器,它是一个频率表,它是所有这些东西,中间没有障碍,没有切换模式也没有单独的传递来运行。
Deflate仍然是两个算法如何结合在一起并相互发挥作用的一个很好的例子,而不是与自己作斗争。
我得承认,我印象深刻。
zip 算法
无意间看到一篇非常好的文档。
压缩和归档的作用
-
mq 传输的时候,数据较大,就需要压缩。(一般网络传输)
-
数据存储,数据量很大的时候。比如数据库,日志就需要归档。
-
这个技术为后期框架提供基础。
个人总结
-
基于信息熵的编码。比如 Huffman 树,数字概率编码。
-
基于字典的编码。游程编码。多元游程编码。
比如:
00001111000
我们约定二进制以0开始,则记为:
443
然后将其转换为二进制:
100 100 011
- 综合使用
实际使用,当然可以把二者结合起来使用。比如 Defalte 算法。
