性别推断
给你一个名字,让你猜这个人的性别是男还是女。
比如:
上官婉儿
吴青峰
相信你可以很容易推断出对应的性别,你是如何做到的呢?如果让你写一个程序来实现,又该如何实现呢?
开源工具
当然,基于名称进行性别推断的开源工具是有的,我们可以先感受一下。
maven 引入
<dependency>
<groupId>com.github.houbb</groupId>
<artifactId>chinese-name</artifactId>
<version>0.0.6</version>
</dependency>
使用
IChineseNameGenderProb genderProb = ChineseNameProbHelper.genderProb("上官婉儿");
Assert.assertEquals("ChineseNameGenderProb{gender=GIRL, prob=0.9780038580012211}", genderProb.toString());
IChineseNameGenderProb genderProb2 = ChineseNameProbHelper.genderProb("吴青峰");
Assert.assertEquals("ChineseNameGenderProb{gender=BOY, prob=0.8912627417339674}", genderProb2.toString());
我们输入姓名,就可以得到对应的性别,及其对应的概率。
那到底是怎么实现的呢?
我们先从最基本的贝叶斯推断说起。
什么是贝叶斯推断
贝叶斯推断(Bayesian inference)是一种统计学方法,用来估计统计量的某种性质。
它是贝叶斯定理(Bayes’ theorem)的应用。
英国数学家托马斯·贝叶斯(Thomas Bayes)在1763年发表的一篇论文中,首先提出了这个定理。
贝叶斯推断与其他统计学推断方法截然不同。
它建立在主观判断的基础上,也就是说,你可以不需要客观证据,先估计一个值,然后根据实际结果不断修正。
ps: 这里也正是统计学的两大学派。贝叶斯学派和频率学派。
计算机诞生以后,它才获得真正的重视。人们发现,许多统计量是无法事先进行客观判断的,而互联网时代出现的大型数据集,再加上高速运算能力,为验证这些统计量提供了方便,也为应用贝叶斯推断创造了条件,它的威力正在日益显现。
贝叶斯定理
要理解贝叶斯推断,必须先理解贝叶斯定理。后者实际上就是计算”条件概率”的公式。
所谓”条件概率”(Conditional probability),就是指在事件B发生的情况下,事件A发生的概率,用 P(A|B) 来表示。
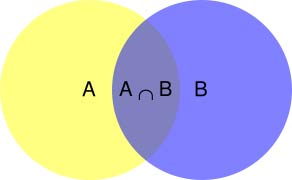
根据文氏图,可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
∵ P(A|B) = P(A∩B)/P(B)
∴ P(A∩B) = P(A|B)P(B)
同理
P(A∩B) = P(B|A)P(A)
∴ P(A|B)P(B) = P(B|A)P(A)
即
P(A|B) = P(B|A)P(A)/P(B)
全概率公式
由于后面要用到,所以除了条件概率以外,这里还要推导全概率公式。
假定样本空间S,是两个事件A与A’的和。

上图中,红色部分是事件A,绿色部分是事件A’,它们共同构成了样本空间S。
在这种情况下,事件B可以划分成两个部分。
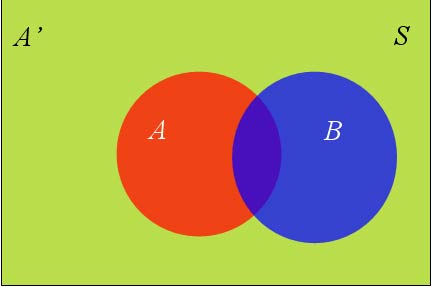
P(B) = P(B∩A) +P(B∩A')
∵ P(B∩A) = P(B|A)P(A)
∴ P(B) = P(B|A)P(A) + P(B|A')P(A')
这就是全概率公式。
它的含义是,如果A和A’构成样本空间的一个划分,那么事件B的概率,就等于A和A’的概率分别乘以B对这两个事件的条件概率之和。
贝叶斯推断的含义
对条件概率公式进行变形,可以得到如下形式:
P(A|B) = P(A)·P(B|A)/P(B)
我们把P(A)称为”先验概率”(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B) 称为”后验概率”(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B) 称为”可能性函数”(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成下面的式子:
后验概率 = 先验概率 x 调整因子
这就是贝叶斯推断的含义。我们先预估一个”先验概率”,然后加入实验结果,看这个实验到底是增强还是削弱了”先验概率”,由此得到更接近事实的”后验概率”。
在这里,如果”可能性函数” P(B|A)/P(B)>1,意味着”先验概率”被增强,事件A的发生的可能性变大;
如果”可能性函数”=1,意味着B事件无助于判断事件A的可能性;如果”可能性函数”<1,意味着”先验概率”被削弱,事件A的可能性变小。
基于贝叶斯的性别推断
贝叶斯公式
| 贝叶斯公式: P(Y | X) = P(X | Y) * P(Y) / P(X) |
| 当X条件独立时, P(X | Y) = P(X1 | Y) * P(X2 | Y) * … |
应用到性别推断上
P(gender=男|name=青峰)
= P(name=青峰|gender=男) * P(gender=男) / P(name=青峰)
= P(name has 青|gender=男) * P(name has 山|gender=男) * P(gender=男) / P(name=青峰)
计算方式
-
怎么算 P(name has 青 gender=男) ?
“青”在男性名字中出现的次数 / 男性字出现的总次数
- 怎么算 P(gender=男)?
男性名出现的次数 / 总次数
- 怎么算 P(name=青峰)?
不用算, 在算概率的时候会互相约去
原因是对于男女而言,这个概率是一样的。所以直接忽略即可。
数据准备
当我们搞定了所有的算法之后,就需要准备基本的数据了。
名字中,基于男/女出现的次数对应的基本数据。
大概的内容如下:
青,54716,48604
峰,232893,16214
婉,1092,10407
儿,1384,3273
分别对应的是
字,男性次数,女性次数
名字的获取
基于中华的特定文化,人的名字由两个部分组成:姓名 = 姓氏 + 名字
姓氏是固定的,不区分男女。你可以基于百家姓等中国的常见姓氏进行剔除,只保留名字。
名字的概率计算
性别字典初始化
我们直接对上述包含不同字及概率的文件进行初始化:
/**
* 男性字出现总数
* @author 老马啸西风
* @since 0.0.2
*/
private static long boyCharTotal;
/**
* 女性字出现总数
* @since 0.0.2
*/
private static long girlCharTotal;
/**
* 男性名字出现的概率
* @since 0.0.2
*/
private static double boyGenderProb;
/**
* 女性名字出现的概率
* @since 0.0.2
*/
private static double girlGenderProb;
/**
* count map
*
* @since 0.0.2
*/
private static Map<Character, Pair<Double, Double>> countMap;
static {
List<String> lines = StreamUtil.readAllLines(ChineseNameConst.LAST_NAME_GENDER_FREQ_PATH);
countMap = Guavas.newHashMap(lines.size());
List<ChineseNameGenderBean> beanList = Guavas.newArrayList(lines.size());
for(String line : lines) {
ChineseNameGenderBean bean = ChineseNameGenderBean.of(line);
boyCharTotal += bean.boyCount();
girlCharTotal += bean.girlCount();
beanList.add(bean);
}
// 频率计算
final double boyCharDouble = boyCharTotal*1.0;
final double girlCharDouble = girlCharTotal*1.0;
final double charTotalDouble = boyCharDouble + girlCharDouble;
boyGenderProb = boyCharDouble / charTotalDouble;
girlGenderProb = girlCharDouble / charTotalDouble;
// 频率在初始化的时候就计算好
for(ChineseNameGenderBean bean : beanList) {
double boyFreq = bean.boyCount() * 1.0 / boyCharDouble;
double girlFreq = bean.girlCount() * 1.0 / girlCharDouble;
Pair<Double, Double> pair = Pair.of(boyFreq, girlFreq);
countMap.put(bean.name(), pair);
}
}
这里主要做了两件事:
(1)计算出 P(gender=性别) 的概率
| (2)计算出 P(name has 青 | gender=男) 的概率。 |
概率的计算
java 实现如下:
//author: 老马啸西风
public double calcProb(GenderEnum genderEnum, String lastName) {
// 根据性别直接计算概率
double prob = getGenderProb(genderEnum);
// 遍历字对应的概率,还是要根据性别计算
// 如果为男性
char[] chars = lastName.toCharArray();
for(char c : chars) {
Pair<Double, Double> pair = countMap.get(c);
if(ObjectUtil.isNull(pair)) {
continue;
}
if(GenderEnum.BOY.equals(genderEnum)) {
prob *= pair.getValueOne();
} else {
// 女
prob *= pair.getValueTwo();
}
}
return prob;
}
getGenderProb 对应的是不同性别的概率,即 P(gender=男)/P(gender=女)。
/**
* 性别对应的概率
* @param genderEnum 性别枚举
* @return 概率结果
* @since 0.0.2
* @author 老马啸西风
*/
private double getGenderProb(final GenderEnum genderEnum) {
if(GenderEnum.BOY.equals(genderEnum)) {
return boyGenderProb;
}
return girlGenderProb;
}
其中 GenderEnum 就是一个普通的枚举值:
public enum GenderEnum {
BOY,
GIRL;
}
工具类封装
完成上面的核心实现之后,我们将其封装为一个便于使用的工具方法。
/**
* @author 老马啸西风
* @since 0.0.1
*/
public final class ChineseNameProbHelper {
private ChineseNameProbHelper(){}
/**
* 推断性别的概率
* @param fullName 全称
* @return 性别的概率推断
* @since 0.0.2
*/
public static IChineseNameGenderProb genderProb(final String fullName) {
String lastName = ChineseNameHelper.lastName(fullName);
return lastNameGenderProb(lastName);
}
/**
* 推断性别的概率
*
* @param lastName 名字
* @return 性别的概率推断
* @since 0.0.4
*/
public static IChineseNameGenderProb lastNameGenderProb(final String lastName) {
ChineseNameBs chineseNameBs = ChineseNameBs.newInstance();
return chineseNameBs.genderProb(lastName);
}
}
小结
贝叶斯在性别推断,垃圾邮件识别,文本聚类等方面还是比较优秀的。
性别推断和文本聚类,老马以前都实现过。
下一节我们来学习下如何实现一个垃圾邮件识别功能。
希望本文对你有所帮助,如果喜欢,欢迎点赞收藏转发一波。
我是老马,期待与你的下次相遇。
