敏感词系列
sensitive-word-admin 敏感词控台 v1.2.0 版本开源
sensitive-word-admin v1.3.0 发布 如何支持分布式部署?
05-敏感词之 DFA 算法(Trie Tree 算法)详解
06-敏感词(脏词) 如何忽略无意义的字符?达到更好的过滤效果
summary
提出了一种新的内部数组结构,称为双数组,实现了 trie 结构。
双数组结合了矩阵形式的快速访问和列表形式的紧凑性。
通过实例介绍检索、插入和删除的算法。
虽然插入比较慢,但还是很实用的,删除和检索的时间都比列表形式有所提升。
通过与各种大key集合列表的比较,双数组的大小可以比列表小17%左右,双数组的检索速度可以从 比列表快3·1到5·1倍。
介绍
在很多信息检索应用中,需要能够采用trie搜索,逐字查找输入。
示例包括编译器的词法分析器、书目搜索、拼写检查器和自然语言处理中的词法词典等。
trie 的每个节点都是一个由下一个“项目”索引的数组。
索引的元素是一个最终状态标志,加上一个指向新节点或空指针的指针。
trie 的检索、删除和插入速度非常快,但需要占用大量空间,因为空间复杂度与节点数和字符数的乘积成正比。
一个众所周知的压缩 trie 的策略是列出弧每个节点的,空指针在列表的末尾。
列表结构的 trie 使我们能够通过使用数组结构的 trie 的空指针来节省空间,但是如果离开每个节点的弧很多,则检索会变慢。
本文提出了一种将 trie 压缩为两个一维数组 BASE 和 CHECK 的技术,称为双数组。
在双数组中,节点 n 的非空位置通过数组 BASE 映射到数组 CHECK 中,使得每个节点中没有两个非空位置映射到 CHECK 中的相同位置。
trie 的每个弧都可以在 0 (1) 时间内从双数组中检索出来,也就是说,对于该键的长度 k,检索键的最坏情况时间复杂度变为 0 ( k )。
trie 有很多节点用于大量键,因此使双数组紧凑很重要。
为了为大量键实现 trie,双数组仅在 trie 中存储消除键歧义所需的前缀,而不需要进一步消除歧义的键的尾部存储在 字符串数组,记为 TAIL。
- Figure 1. An array-structured trie for bachelor, baby, badge, jar
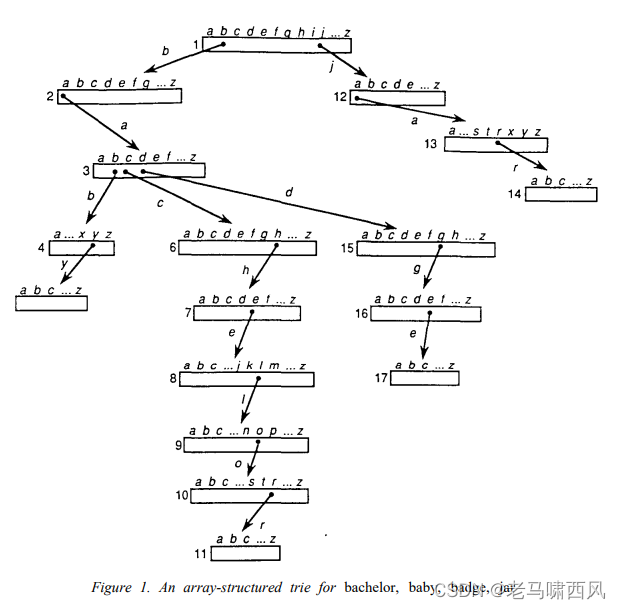
- Figure 2. A list-structured trie for bachelor, baby, badge, jar
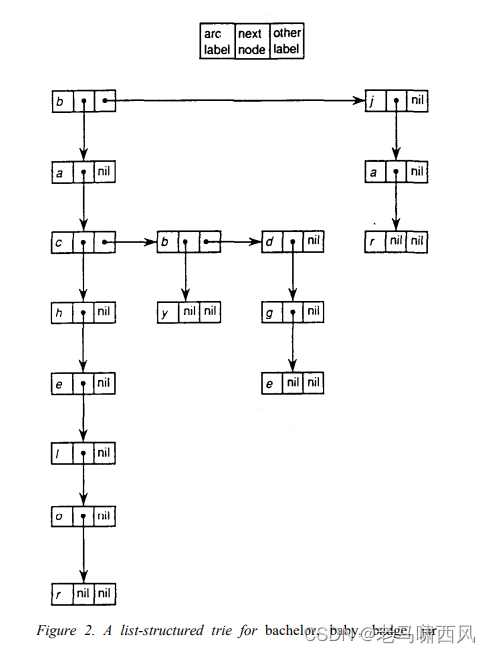
TRIE 的表示
trie 是一种树结构,其中从根到叶子的每条路径对应于表示集中的一个键。
trie 中的路径对应于集合中键的字符。
为避免将“the”和“then”等词混淆,在集合中每个词的末尾使用了一个特殊的结束标记符号 #。
以下定义将用于以下解释。
K 是由 trie 表示的键集。
trie 由节点和弧组成。 弧标签由称为字符的符号组成。 从节点 n 到 m 标记为 a 的弧由符号 g(n, a)=m 表示。
对于 K 中的键,如果 a 是足以将该键与 K 中的所有其他键区分开来的字符(或弧标签),则具有 g(n,a)=m 的节点 m 是一个单独的节点。
从单独节点 m 到终端节点的弧标签的串联称为 m 的单个字符串,表示为 STR[ m ]。
从 K 中删除单个字符串后剩下的键 K 的字符称为 K 的尾部。
仅由从根到 K 中所有键的单独节点的弧构成的树称为缩减特里树。
图 3 显示了集合 K= {baby#, bachelor#, badge#, jar#} 的简化 trie 示例。
图 3 中也显示了相同的简化 trie 表示,使用双数组和字符数组进行尾部存储。
TAIL中的问号(?)表示垃圾; 它们的用途将在分析插入和删除算法时进行解释。
简化的 trie 和图 3 所示的双数组之间存在以下关系:
- Figure 3. The reduced trie and the double-array for K
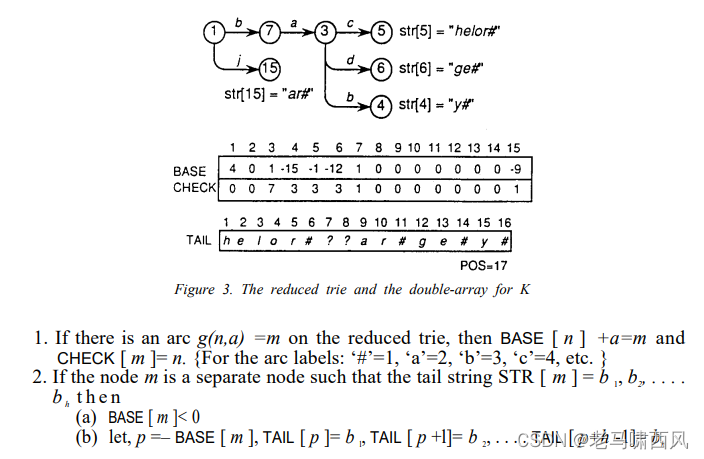
这两种关系将贯穿本文。
检索(Retrieval)
使用双数组的检索操作很简单。
例如,到从图3所示的双数组中检索’bachelor#’,以下步骤执行:
1) 将根节点存储在双数组中 BASE 的位置 1,并从该位置开始。
字符 ‘b’ 的值为 3,因此从上面的关系
BASE [ n ]+ a =BASE [ l]+ ‘b’= BASE [l]+3=4+3=7
观察 CHECK [7] = 1 因为为 B 找到的值
2) 观察 CHECK [7] = 1 由于在步骤 1 中为 BASE 找到的值为正,因此继续。
使用步骤 1 中的值 7 作为 BASE 的新索引,并使用字符“a”的值 2,因此:
BASE [7]+ ‘a’= BASE [7] +2=l+2=3, and CHECK [3]=7
3) 如上所述,使用 4 作为“c”:
BASE [3]+ ‘c’= BASE [3]+4=1+4=5, and CHECK [5]=3
BASE [5] 中的值为 – 1。负值表示单词的其余部分位于 TAIL 中,从 TAIL [– BASE [5]] = TAIL [l] 开始。
可以使用类似的技术检索列表中的其他单词,始终从 BASE 中位置 1 的根节点开始。
观察到检索只涉及直接数组查找(不需要搜索)和加法,使得检索在这个实现中非常高效。
PS: 这里感觉并没有使用到 check 数组。
插入 (insert)
插入双数组也很简单。
在插入过程中,会出现以下四种情况中的任意一种:
-
双数组为空时插入新词。
-
插入新词没有任何冲突。
-
插入新词并发生碰撞; 在这种情况下,必须向 BASE 添加其他字符,并且必须从 TAIL 数组中删除字符以解决冲突,但必须删除 BASE 数组中已有的任何内容。
-
当插入新词并发生如情况 3 中的冲突时,必须移动 BASE 数组中的值。
冲突表示两个不同的字符在双数组中具有相同的索引值。
这四个插入案例将通过添加 ‘bachelor’(案例 1)、’jar#’(案例 2)、’badge#’(案例 3)和 ‘baby#’(案例 4)到一个空的双数组结构来演示 如图 4 所示。
我们将 double 数组的大小定义为 DA_SIZE 表示的 CHECK 非零条目的最大索引。
请注意,如果需要,可以将超过 DA_SIZE 的 BASE 和 CHECK 条目动态分配为零条目。
情况一:双数组为空时插入新词
要插入例如“bachelor#”,请执行以下步骤:
步骤 1. 从双数组中 BASE 的位置 1 开始。 字符“b”的值为 3,因此:
BASE [1]+‘b’ =BASE [1]+3=1+3=4, and CHECK [4]=0 != 1
步骤 2. CHECK [4] 中的值 0 表示插入了单词的其余部分。
也就是说,‘b’是在双数组上定义的(通过关系 g(l,‘b’) =4),因此将剩余的字符串‘achelor#’存储到 TAIL 中。
- Figure 4. The reduced trie and the double-array with no data
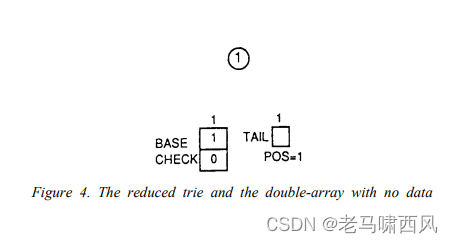
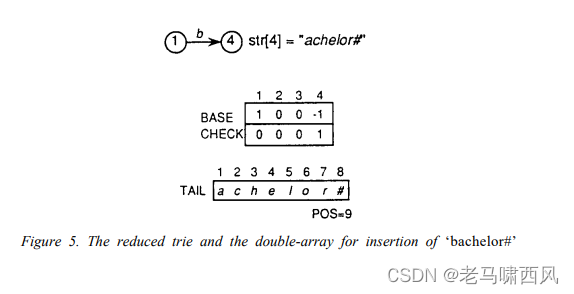
Step 3. 设置 BASE [4] <- – POS =–1 表示该词的其余部分从位置 POS 开始存储到 TAIL 中。
并在双数组中设置 CHECK [4] <- 1 以指示它来自的节点号。
步骤 4. 将指针设置为 TAIL POS <- 9,这是下一次插入的位置。
PS: 为啥是 9 呢?个人理解 achelor# 的长度为 8,所以下次从位置9开始。这里的下标不是从0开始的,而是从1
- Figure 5 shows the reduced trie and the double-array after inserting ‘bachelor#’.
情况 2:插入,插入新词时没有碰撞
执行以下步骤以插入“jar#”:
步骤 1. 从双数组中 BASE 的位置 1 开始。
字符‘j’的值为 11,因此:
BASE [l]+‘j’= BASE [1]+11=1+11=12, and CHECK [12]= 0 != l
步骤 2. CHECK [12] 中的值 0 表示插入了单词的其余部分,这意味着没有与“bachelor#”发生冲突。
将剩余的字符串“ar#”从位置 POS = 9 存储到 TAIL 中。
步骤 3. 设置
BASE [12] <- -POS =-9
Step 4. 将指针设置为 TAIL POS <- 12,这是下一次插入的位置。
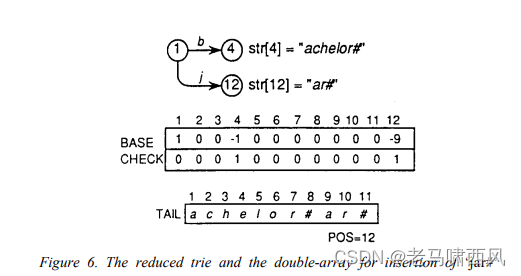
可以看出,案例 1 和案例 2 的插入之间没有区别,因此它们的分类只是概念性的,而不是操作性的。
插入“jar#”后生成的简化 trie 和双数组如图 6 所示。
- Figure 6. The reduced trie and the double-array for insertion of ‘jar#’
要研究返回插入情况 3 和 4,请考虑函数 X_CHECK(LIST),其中最小整数 q 使得 q> 0 并且 ` CHECK [ q+c ] =0` 用于 LIST 中的所有 c。
q 总是以值 1 开始,并且在分析时具有单位增量。
情况 3:插入,当发生碰撞时对‘badge#’执行以下步骤:
步骤 1. 从字符“b”中 BASE 的位置 1 开始为 3,因此:
BASE [l]+‘b’= BASE [l]+3=l+3=4, and CHECK [4]=1
CHECK[4]中的非零值表示存在从CHECK[4]中的值所指示的节点即1到节点4的弧定义.
步骤 2. 由于在步骤 1 中为 BASE 找到的值为正,因此继续。 第 1 步中的值 4 用作 BASE 的新索引,但是:
BASE [4]=–1
这个负值表示搜索已经完成,要进行字符串比较。
步骤 3. 从 TAIL 中检索从位置 – BASE [4] = 1 开始的字符串,即‘achelor#’,并将其与要插入的字符串的剩余部分,即‘adge#’进行比较。
由于比较失败,即字符串彼此不同,将公共前缀插入到双数组中,如步骤 4、5 和 6 所示。
ps: 如果这里相同,则很简单,但是不同,所以我们要看一下如何处理?
步骤 4. 将 BASE [4] 的当前值保存到时间变量中:
TEMP <- BASE [4]=1
ps: 避免这个值被覆盖丢失。
步骤5:公共前缀计算
为两者共有的前缀字符’a’计算X_CHECK[{‘a’}]
字符串‘adge#’和‘achelor#’:
CHECK [ q+a ]= CHECK [ l+‘a’] = CHECK [l+2]= CHECK [3]=0
q的值,即1,是BASE[4]的新值的候选,CHECK[3]的值为0表示节点3可用,所以:
步骤6:存储 BASE [4] 的新值:
BASE [4] <- q = 1
以及可用节点 3 的 CHECK 的新值:
CHECK [ BASE [4]+'a'] = CHECK [l+2] = CHECK [3] <- 4
这表示从 CHECK [3] 中的节点值即 4 到节点 3 的弧定义。
注意:由于本例中的前缀是公共的,因此不再重复步骤5和6,但是这两个步骤必须在前缀值存在的情况下执行多次。
步骤7:要存储剩余的字符串 ‘chelor#’ 和 ‘dge#’,根据 X_CHECK ( {‘c’ ,’’} ) 如下。
For ‘c’: CHECK [q+‘c’] = CHECK [l +4] = CHECK [5] =0 => available
For ‘d’: CHECK [q+‘d’] = CHECK [l+5]= CHECK [6] =0 => available
因为 q= 1 是可选项, set
BASE [3] <- 1
步骤8:计算节点号 CHECK,以引用 BASE 中的“chelor#”和字符串的第一个字符作为参数:
BASE [3]+‘c’=1+4=5
BASE [5] <- –TEMP= –1 and CHECK [5] <- 3
通过 BASE 建立对 TAIL 的引用,通过 CHECK 建立状态 3 和 5 之间的弧定义。
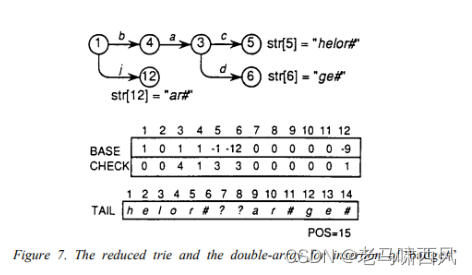
步骤9:将字符串“helor#”的其余部分从位置 BASE [5] = 1 开始存储到 TAIL 中,但 TAIL [7] 和 TAIL [8] 在图 7 中变成垃圾(garbage)。
- Figure 7. The reduced trie and the double-array for insertion of ‘badge#’
步骤10:至于剩下的另一个字符串 dge#
BASE [3]+‘d’=l+5=6
BASE [6] <- – POS = – 12 and CHECK [6] <- 3
从 POS 开始将“ge#”存储到 TAIL 中。
步骤11:最后将 POS 设置为新的插入位置,在 TAIL 已使用部分的末尾。
POS <- 12+length[‘ge# ’]=12+3=15
总之,当发生冲突时,冲突字符串的公共前缀从 TAIL 中提取并插入到双数组中。
碰撞字符串(包括新字符串)的双数组中的值被移动到可用的最近邻位置并调整到此类新位置(参见图 7)。
情况 4:插入,当插入一个新词时发生碰撞
与情况 3 一样,必须移动 BASE 数组中的值; 对“baby#”执行以下步骤:
Step 1. 根节点存储在双数组中BASE的位置1,所以从位置1开始。
对于前三个字符,BASE 和 CHECK 的值为:
BASE [l]+‘b’= BASE [l]+3=l+3=4, and CHECK [4]=1
BASE [4]+‘a’= BASE [4] +2=l+2=3, and CHECK [3]=4
BASE [3]+‘b’= BASE [3 ]+3=l+3=4, and CHECK [4]=1 != 3
CHECK [4] 中的不一致表示未定义状态,这意味着应该修改节点 1 和 3 的值以允许新的插入,因此进行如下操作。
步骤 2. 将临时变量 TEMP_NODE1 设置为
TEMP_NODE1 <- BASE [ 3]+ ‘b’=1+3=4
如果 CHECK [4] 等于 0 那么这将意味着可用性,因此这种情况将是在 POS 处将字符串直接插入到 TAIL 中。
由于情况并非如此,请执行以下操作。
步骤 3. 存储在一个列表中,索引号是发现不一致的节点号,对应于离开该节点的弧的字符
LlST [3] <- [‘c’,‘d’]
在另一个列表中,以最后一个 CHECK 值作为索引,对应于离开该节点的弧的字符。
LIST [l] <- [‘b’,‘j’]
步骤 4. 由于此处的目的是将新字符串与节点 3 相关联,因此比较两个列表的长度,将 LIST [3] 的长度递增 1。
此增量对于考虑要添加到节点 3 的新字符是必要的。
compare (length [ LIST [3]]+ 1, length [ LIST [l]])= compare (3,2)
如果 length [ LIST [3]]+ 1 < length [ LIST [l]] 当前节点 3 将被修改。
但是作为 length [ LIST [3]] + 1 >= length [ LIST [l]] 修改备选节点,即节点1,如下
步骤 5. 为 BASE 引用的节点设置临时变量
TEMP_BASE <- BASE [l]=l
并根据可用的最近邻居使用 LIST [l] 计算新的 BASE,如下所示:
X_CHECK [‘b’]: CHECK [q+‘b’]
= CHECK [1+3] =CHECK [4]=l != 0
CHECK [2+3] =CHECK [5]=–l != 0
CHECK [3+3] =CHECK [6]=–14 != 0
CHECK [4+3] =CHECK [7]=0 => available
and
X_CHECK [‘j’]: CHECK [q+‘j’] = CHECK [4+11]=CHECK [15]
=0 => available
因为 q = 4 是候选者,所以设置
BASE [1] <- 4
步骤 6. 对于“b”,将要修改的状态的值存储在临时变量中:
TEMP_NODE1 <- TEMP_BASE+ ‘b’ =1+3=4
TEMP_NODE2 <- BASE[1]+ ‘b’=4+3=7
将 BASE 值从原始状态复制到新状态:
BASE[TEMP_NODE2] <- BASE[TEMP_NODE1]
i.e.
BASE [7] <- BASE [4] = 1
并为新节点设置 CHECK 值:
CHECK [ TEMP_NODE2 ] =CHECK [7] <- CHECK [4]=1
步骤 7. 因为 BASE[TEMP_NODE1] = BASE [4]=1>0
即原始状态的BASE值是一个内部指针而不是指向TAIL的指针,计算偏移w得到要修改的节点值指向新节点
CHECK [ BASE ] TEMP_ NODE1 ]+ w ] =TEMP_NODE1
i.e.
CHECK [ BASE [4]+ w ]=4; CHECK [1+ w ] = 4 => w =2
并修改 CHECK 以指向新状态:
CHECK [ BASE [4]+2] = CHECK [l+2]= CHECK [3] => TEMP_NODE2 =7
步骤 8. 初始化旧的 BASE 并检查:
BASE [ TEMP_NODE1 ] = BASE [4] <- 0
CHECK [ TEMP_NODE1 ] = CHECK [4] <- 0
步骤 9. 对于“j”,将要修改的状态的值存储在时间变量中:
TEMP_NODE1 <- TEMP_BASE + ‘j’ =1+11=12
TEMP_NODE2 <- BASE [1]+ ‘j’ =4+11=15
将 BASE 值从原始状态复制到新状态:
BASE [ TEMP_NODE2 <- BASE [ TEMP_NODE1 ]
i.e.
BASE [15] <- BASE [12]=-9
并为新节点设置 CHECK 值:
CHECK [ TEMP_NODE2 ] = CHECK [15] <- CHECK [12]=1
步骤10:因为
BASE [ TEMP_NODE1 ] =BASE [12]=–9<0
也就是说,原始状态的 BASE 值是指向 TAIL 的指针,因此只需初始化旧的 BASE 和 CHECK:
BASE [ TEMP_NODE1 ] = BASE [12] <- 0
CHECK [ TEMP_NODE1 ] = CHECK [12 ] <- 0
现在baby ‘b’碰撞产生的冲突已经解决了。 最后,将新字符串“by#”的剩余部分插入到 TAIL 中。
第 11 步。考虑原始 BASE 节点号,即 3,其中产生不一致(参见第 3 步)作为主元(pivot),将节点号存储在时间变量中以引用新字符串:
TEMP_NODE <- BASE [3]+ ‘b’= 1+3=4
第 12 步。在新的 BASE 节点中存储指向新字符串的 TAIL 的指针:
BASE [ TEMP_NODE ] =BASE [4] <- – POS =–15
并检查指向引用节点的内部指针
CHECK [ TEMP_NODE ] =CHECK [4] <- 3
第 13 步。在 TAIL 中插入新字符串:
TAIL [ POS ] =TAIL [15] +‘y#’
第 14 步。要完成,将指向 TAIL 的指针设置为其新值:
POS <- POS+ length [’y#’] = 15+2= 17
总之,当发生冲突时,必须移动双数组中的值,因为没有空间指定新词、冲突的节点或前一个节点,如 CHECK 所示。
然后将具有较少分支的节点移动到双数组中的另一个位置,以便为冲突节点指定更多节点提供空间。
连接节点编号被修改为指向双数组中移动节点规范的新位置。
最后,插入新字符串(参见图 3)。
删除 (Deletion)
从双数组中删除单词也很简单。 删除与情况 2 插入具有相同的扫描过程。
事实上,唯一的区别在于为要删除的单词重置双数组中指向 TAIL 的必要指针。
例如,要删除单词“badge#”,请执行以下操作:第 1 步。
根节点存储在双数组中 BASE 的位置 1,因此从位置 1 开始。
对于前三个字符,BASE 和 CHECK 的值为
BASE [1]+‘b’= BASE [1]+3=4+3=7, and CHECK [7]=1
BASE [7]+‘a’= BASE [7]+2=l+2=3, and CHECK [3]=7
BASE [3]+‘d’=BASE [3]+5=l+5=6, and CHECK [6]=3
BASE [6] = – 12<0 => separate node
单独的节点是指向 TAIL 的指针。
步骤 2. 比较字符串的剩余部分,即“ge#”与 TAIL 中位于 –BASE [6]=12 的字符串
compare (‘ge#’,’ge#’)
步骤 3. 由于两个字符串相等,因此将相应的指针重置为双数组中的 TAIL。
BASE [6] <- 0
CHECK [6] <- 0
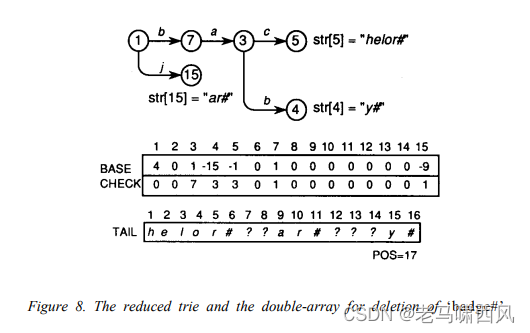
由于指向 TAIL ‘ge#’ 的指针变为垃圾,因为 ‘ge#’ 在图 8 中不存在,因此空间可供将来使用
- Figure 8. The reduced trie and the double-array for deletion of ‘badge#’
EVALUATION
对比 list
trie 的一个众所周知的表示是使用 more,TAIL 的部分为可供将来使用的列表形式。
虽然列表可以高效地压缩和更新trie,但其访问速度较慢。
假设reduced trie的每个节点号都是用两个字节来实现的。
每个节点在双数组中占用四个字节,在列表形式中占用五个字节(基于组件 arc label, pointer, next node )。
一个合理的折衷方案是将最常用的节点(例如根节点)存储为直接访问表,其中可以通过使用当前输入符号直接索引到表中来确定下一个节点,并将其他节点存储在列表中 形式。
在模拟中,也在本文中,这种修改后的列表形式用于简化的 trie,并将单个字符串存储到 TAIL 中。
以下五种键组用于实验过程。
KW1,KW2:分别是Pascal和COBOL的保留字。 KW3:UNIX 4.2BSD 中的命令。 KW4:世界主要城市名称。 KW5:日语词典的片假名。 KW6:英语词典的单词。 KW7:日语词典的汉字
- Table I. The results of storage
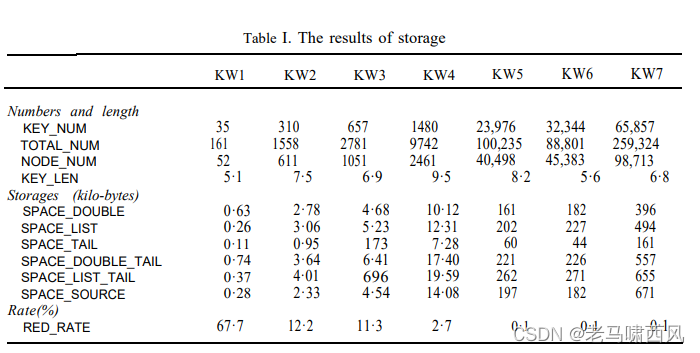
请注意,KW5–KW7 的双数组分为几个块,以保留双数组和列表形式的双字节条目。
空间效率
表一中,KEY_NUM为key的个数; TOTAL_NUM 是未缩减的 trie 中的节点数; NODE_NUM 是缩减的 trie 的节点数; KEY_LEN 是密钥的平均长度。
SPACE_DOUBLE 代表减少的 trie 的双数组存储; SPACE_LIST 用于存储简化的 trie 的列表形式; SPACE_TAlL 用于存储 TAIL; SPACE_DOUBLE_TAIL用于存储SPACE_DOUBLE加上SPACE_TAIL; SPACE_LIST_TAIL 用于存储SPACE_LIST加上SPACE_TAIL; 和 SPACE_SOURCE 用于存储所有键的源文件,键之间有分隔符。
请注意,TAIL 已重新组织以删除冗余字符。
RED_RATE表示最终双数组的冗余索引数占NODE_NUM的百分比,即表示所提出的压缩方法的空间效率。
从表一的结果可以看出,对于除KW1之外的所有集合,双数组的SPACE_DOUBLE_TAIL中的存储量比列表形式的SPACE_LIST_TAlL中的存储量少约8%到17%。
特别是,存储结果显示 SPACE_DOUBLE_TAIL 仅比大型集合的 SPACE_SOURCE 大 1.1 到 1.2 倍。
这取决于大型集合的双阵列的极小 RED_RATE。
时间效率
所提出算法的关键概念是,在案例 4 插入期间,只有一部分 trie(trie 中发生碰撞的部分,具有较少的弧)必须移动到 BASE 中第一个可用的空白位置,该位置足够大 拿着那块。
这使得插入操作变得昂贵,但只有一个部分被移动的事实是插入成本不会变成 n 个状态的 O ( n 2 ) 的原因。
所提出的插入算法的最坏情况时间复杂度取决于在情况 4 插入时调用的函数 X_CHECK(LIST),因为它遍历双数组的所有索引以搜索 LIST 中每个符号的可用位置。
对于几百个以下的小键组,插入可以保持实用的速度,但是对于大键组,插入速度会变慢。
为了避免开销,具有连接可用索引或冗余索引的双向链接的双数组被引入如下。
让 r1, r2, ….., rm 是 doublearray 上可用索引的递增顺序:
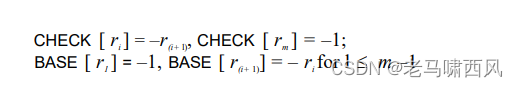
其中值 – 1 表示两个链接的每一端。 两个链接的每个头都由全局变量表示。
请注意,CHECK 数组中的可用条目必须由负整数而不是零来确认,并且双数组的初始化条目需要将这些条目附加到链接中。
本次修改比较简单,与双数组占用的空间无关,所以后面的评测使用修改后的双数组
结论
已经提出了表示 trie 结构的双数组结构。
对于各种键,通过比较列表形式评估了双数组的空间和时间效率。
double 数组可以构建快速紧凑的字典,但当 double 数组中存储了很多键时,插入速度比列表形式慢。
在实际实现大量密钥时,应该将双数组分成适当的块存储到辅助中 记忆。
这种划分对于限制在主存中的一个工作区的应用软件是有用的,并且能够实现快速插入,因为每个划分的双数组保持合理数量的键。
递增地构建用于自然语言处理的词典很重要,因为可能需要不时地向已建立的基本词汇表添加额外的词。
这里提出的算法适用于追加关键字频率高于删除关键字频率的信息检索系统,允许删除产生的冗余空间被后续插入耗尽。
所呈现的双数组已用于大约 40 组动态键(即动态命令解释器、用于机器翻译系统的书目搜索日语和英语形态词典、7 过滤高频英语单词 6 和拼写检查器 6 发射校正 候选人等)。
double-array可以高效地操纵基于trie的最长适用匹配,因此非常适合分析没有单词间分隔符的日语句子。
将此处介绍的用于更新双数组的算法应用于具有故障功能的模式匹配机将是一项非常有趣的研究; 5 通过使用行位移减少静态稀疏矩阵 9,10; 与解析表关联的有限状态机; 等等。
参考资料
http://www.co-ding.com/assets/pdf/dat.pdf
