什么是波兰表达式
我们日常的运算表达式通常是如下形式,这种成为中缀表达式,也就是运算符在运算数的中间。
这种表达式人类很容易识别,并根据其进行计算,但计算机识别这种表达式非常困难。
a + b * (c - d) + e/f
逆波兰表达式
概念
为什么叫逆波兰表达式呢?
首先是波兰数理学家 Jan Łukasiewicz 想到的这种表达数学算式的方法,其次相对于将运算符放在数字间的正常的算式表达方式,该方法采用将运算符号放在数字后面的表达方式(同时还省略所有的括号)。所以叫逆波兰表达式
例子
9+(3-1)*3+10/2 的逆波兰表达式为:9 3 1 - 3 * + 10 2 / +
其实就是将算式的中缀形式改为后缀形式,那么我们怎么根据一个表达式来得到对应的逆波兰表达式呢?
如何得到
思想(利用栈的先进后出思想):
从左到右遍历中缀表达式的每一个数字和符号,如果是数字,那么就输出,如果是算术符号,则判断其和栈顶符号的优先级,如果是右括号或者是优先级低于栈顶符号优先级,则将栈内的符号出栈,将当前符号入栈,一直到结束。
推导:9+(3-1)*3+10/2
输出9 -> 输出值:9
+ 入栈 -> 栈内:+
( 入栈 -> 栈内:+ (
输出3 -> 输出值:9 3
-入栈 -> 栈内:+ ( -
输出1 -> 输出值:9 3 1
此时是符号),栈内符号出栈至(,输出值:9 3 1 -,栈内:+。其中()不打印
此时是符号*,优先级大于+,入栈->栈内:+ *
输出3 -> 输出值:9 3 1 - 3
此时是符号+,优先级小于*,出栈->输出:9 3 1 - 3 * +,然后+入栈 -> 栈内:+
输出10 -> 输出值:9 3 1 - 3 * + 10
/入栈 -> 栈内:+ /
输出2 -> 输出值:9 3 1 - 3 * + 10 2
算式结束,将栈内符号出栈 -> 输出值:9 3 1 - 3 * + 10 2 / +
结束,最终得到逆波兰表达式:9 3 1 - 3 * + 10 2 / +
C 实现
#include <stdio.h>
#include <string.h>
struct Node
{
char data[1000];
int top = -1;
}stack;
int isPriority(char a, char top);
int main(int argc, char const *argv[])
{
char str[1000];
gets(str);
int len = strlen(str);
for(int i=0; i<strlen(str); i++){
if(str[i]>=48 && str[i]<=57){//输出数字
if(i<strlen(str)-1 && (str[i+1]>=48 && str[i+1]<=57)){
printf("%c", str[i]);
}else{
printf("%c ", str[i]);
}
}else{//入栈或者出栈
if(stack.top==-1 || isPriority(str[i], stack.data[stack.top])){//当前运算符优先级不低于栈顶优先级
//入栈
stack.data[++stack.top] = str[i];
}else{
if(str[i] == ')'){//出栈至'('
while (stack.data[stack.top] != '('){
printf("%c ", stack.data[stack.top]);
stack.top--;
}
stack.top--;//将'('出栈但是不输出
}else{//全部出栈
while (stack.top != -1){
printf("%c ", stack.data[stack.top]);
stack.top--;
}
//当前符号入栈
stack.data[++stack.top] = str[i];
}
}
}
}
//全部出栈
while (stack.top != -1){
printf("%c ", stack.data[stack.top]);
stack.top--;
}
return 0;
}
int isPriority(char a, char top){
//判断a运算符和栈顶top运算符的优先级,如果a不低于栈顶top,输出1,否则输出0
if(((a=='+')||(a=='-')) && ((top=='*')||(top=='/')) || a == ')'){//低于栈顶优先级
return 0;
}
return 1;
}
逆波兰表达式的计算
逆波兰表达式的计算就比较简单了。以上面结果中的队列为输入,同时再准备一个栈用于运算。
具体流程如下:
-
将队列中的数据依次出队,然后压栈;
-
在出队的过程中如果遇到运算符,则从栈中弹出2个运算数,分别作为右运算数和左运算数,进行运算;
-
将步骤2的运算结果入栈;
-
跳入步骤1,继续进行出队操作。
依然以上述内容为例进行介绍。
如图1中第一行左侧为形成的队列,右侧是一个空栈。将队列中操作数依次出队,入栈。
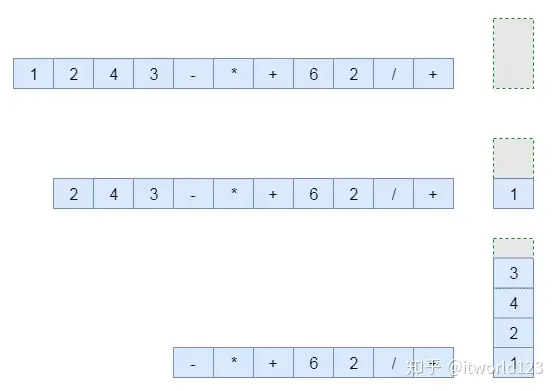
在出队的过程中遇到运算符(-),此时将操作数出栈进行运算(注意这里操作数的顺序)。
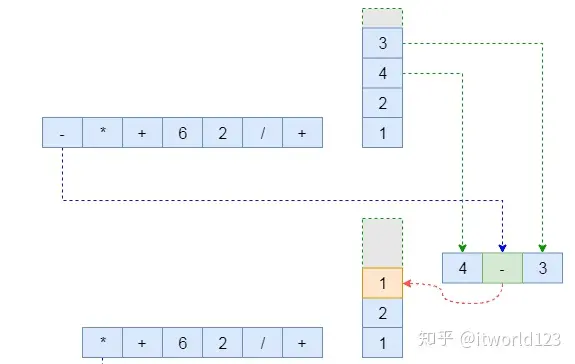
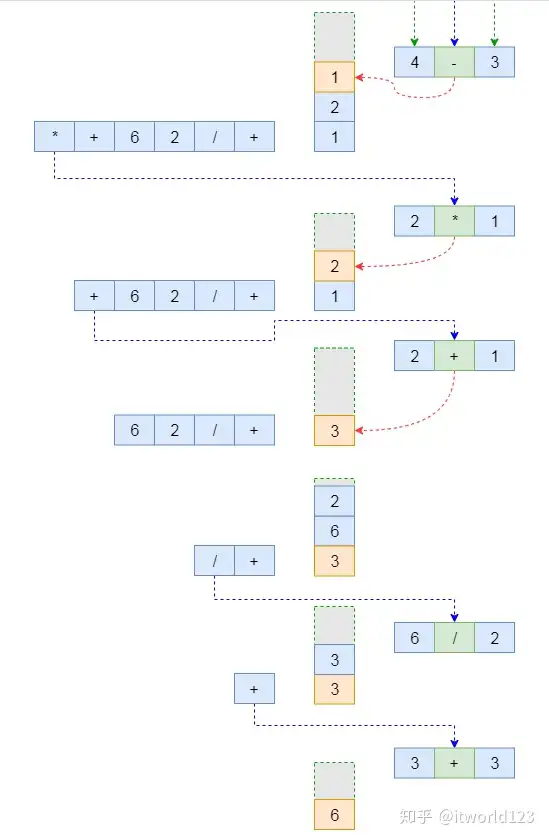
重复上述操作,直到将队列中所有内容出队。
leetcode 150 Evaluate Reverse Polish Notation
题目
You are given an array of strings tokens that represents an arithmetic expression in a Reverse Polish Notation.
Evaluate the expression. Return an integer that represents the value of the expression.
Note that:
The valid operators are ‘+’, ‘-‘, ‘*’, and ‘/’. Each operand may be an integer or another expression. The division between two integers always truncates toward zero. There will not be any division by zero. The input represents a valid arithmetic expression in a reverse polish notation. The answer and all the intermediate calculations can be represented in a 32-bit integer.
Ex
Example 1:
Input: tokens = ["2","1","+","3","*"]
Output: 9
Explanation: ((2 + 1) * 3) = 9
Example 2:
Input: tokens = ["4","13","5","/","+"]
Output: 6
Explanation: (4 + (13 / 5)) = 6
Example 3:
Input: tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
Output: 22
Explanation: ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
Constraints:
1 <= tokens.length <= 10^4
tokens[i] is either an operator: “+”, “-“, “*”, or “/”, or an integer in the range [-200, 200].
V1-基本思路
思路
结合上面的计算方式,我们直接把遍历 string[],如果是数字就一直压入栈 stack 内。
如果遇到操作符,则 top2 操作符 top1,然后把结果 result 继续压入栈内,重复上面的步骤。
直接 string[] 遍历完成,且 stack 也空了输出结果。
实现
import java.util.Stack;
public class T150_EvaluateReversePolishNotation {
/**
* 1. 遍历 tokens,压入 stack 内
*
* @param tokens 字符串数组
* @return 结果
*/
public int evalRPN(String[] tokens) {
String operators = "+-*/";
Stack<String> stack = new Stack<>();
int result = 0;
// 是否为操作符
for(String token : tokens) {
// 操作符
if(operators.contains(token)) {
String top1 = stack.pop();
String top2 = stack.pop();
// 计算的时候,top2 要在前面
result = calc(top2, token, top1);
// 把结果压入栈
stack.add(result+"");
} else {
// 数字压入栈内
stack.add(token);
}
}
// 最后的出栈
result = Integer.parseInt(stack.pop());
return result;
}
private int calc(String top2, String operator, String top1) {
switch (operator) {
case "+":
return Integer.parseInt(top2) + Integer.parseInt(top1);
case "-":
return Integer.parseInt(top2) - Integer.parseInt(top1);
case "*":
return Integer.parseInt(top2) * Integer.parseInt(top1);
case "/":
return Integer.parseInt(top2) / Integer.parseInt(top1);
default:
throw new UnsupportedOperationException();
}
}
}
V2-更强的算法
上面的方法,是根据原理,推出的实现,不过看了其他大佬的解法,很强。
实现如下:
class Solution {
int idx;
public int evalRPN(String[] tokens) {
idx = tokens.length - 1;
return eval(tokens);
}
private int eval(String[] tokens) {
if(!isOperator(tokens[idx]))
return Integer.valueOf(tokens[idx--]);
char operator = tokens[idx--].charAt(0);
int right = eval(tokens);
int left = eval(tokens);
if(operator == '+') return left + right;
if(operator == '-') return left - right;
if(operator == '*') return left * right;
if(operator == '/') return left / right;
return -1;
}
private boolean isOperator(String token) {
if(token.length() > 1) return false;
char c = token.charAt(0);
return c == '+' || c == '-' || c == '*' || c == '/';
}
}
这种就是模拟 stack 的流程,从 tokens 的后面往前遍历。
然后递归调用处理。
参考资料
https://zhuanlan.zhihu.com/p/65110137
https://zhuanlan.zhihu.com/p/94431722
https://leetcode.com/problems/evaluate-reverse-polish-notation/
