214. 最短回文串
给定一个字符串 s,你可以通过在字符串前面添加字符将其转换为回文串。找到并返回可以用这种方式转换的最短回文串。
示例 1:
输入:s = "aacecaaa"
输出:"aaacecaaa"
示例 2:
输入:s = "abcd"
输出:"dcbabcd"
```
提示:
0 <= s.length <= 5 * 10^4
s 仅由小写英文字母组成
# 基础
是否为回文的基本方法:
```java
/**
* 是否为回文
*
* @param string 字符串
* @return 是否
*/
public static boolean isPalindrome(final String string) {
if (string.length() == 1) {
return false;
}
final int length = string.length();
int mid = length >> 1;
for (int i = 0; i < mid; i++) {
if (string.charAt(i) != string.charAt(length - i - 1)) {
return false;
}
}
return true;
}
v1-翻转暴力法
思路
任何一个字符串,比如 abcd,我们把它翻转得到 dcba,拼接在一起 dcbabcd,肯定是一个回文。
当然,这样不是最短的。
比如 aacecaaa,只需要前面加一个 a 即可。
我们可以考虑从原始字符串的最后一位开始,向前逐步拼接,判断完整的字符串是否为回文。
java 实现
class Solution {
public String shortestPalindrome(String s) {
// 本身就是
if(isPalindrome(s)) {
return s;
}
StringBuilder builder = new StringBuilder();
for(int i = s.length()-1; i >=0; i--) {
builder.append(s.charAt(i));
String newStr = builder + s;
if(isPalindrome(newStr)) {
return newStr;
}
}
return "";
}
/**
* 是否为回文
*
* @param string 字符串
* @return 是否
*/
public static boolean isPalindrome(final String string) {
if (string.length() == 1) {
return true;
}
final int length = string.length();
int mid = length >> 1;
for (int i = 0; i < mid; i++) {
if (string.charAt(i) != string.charAt(length - i - 1)) {
return false;
}
}
return true;
}
}
这个方法的 TC 为 O(N^2),正常还行。
但是本题目难度为 hard,在 120/121 的测试用例直接超时。
V2-最长回文前缀暴力法
思路
比如 aacecaaa,只需要前面加一个 a 即可。
实际上我们需要从头开始寻找前面的最长回文子串,比如 aacecaaa 从头开始,最长的回文子串是 aacecaa。
只需要把剩余的部分翻转,加到开头即可。
当然,如果 adcd 这种都不是的,其实不需要从 0 开始截取翻转,从 1 就行。因为 0 这个位置的,可以当做回文的中间字符,短一点。
初步实现
class Solution {
public String shortestPalindrome(String s) {
// 本身就是
if(isPalindrome(s)) {
return s;
}
// 从头开始,寻找最长的回文子串。
StringBuilder stringBuilder = new StringBuilder(s);
//从末尾开始,逐步删除1位
for(int i = s.length()-1; i >= 0; i--) {
stringBuilder.deleteCharAt(i);
// 判断是否为回文
if(isPalindrome(stringBuilder.toString())) {
break;
}
}
// 如果 abcd 都不是回文,那么其实是从 1 开始,因为第一个可以当中间。 bcd => dc b cd
// 减去剩下的,翻转加到开始
int len = Math.max(1, stringBuilder.length());
String remainStr = s.substring(len);
return new StringBuilder(remainStr).reverse() + s;
}
/**
* 是否为回文
*
* @param string 字符串
* @return 是否
*/
public static boolean isPalindrome(final String string) {
if (string.length() == 1) {
return false;
}
final int length = string.length();
int mid = length >> 1;
for (int i = 0; i < mid; i++) {
if (string.charAt(i) != string.charAt(length - i - 1)) {
return false;
}
}
return true;
}
}
当然,换一种思路,TC 是 O(N^2),所以依然会在 120/121 超时。
V3-哈希法
思路
我们可以用 Rabin-Karp 字符串哈希算法来找出最长的回文串。
在该方法中,我们将字符串看成一个 base 进制的数,它对应的十进制值就是哈希值。
显然,两个字符串的哈希值相等,当且仅当这两个字符串本身相同。然而如果字符串本身很长,其对应的十进制值在大多数语言中无法使用内置的整数类型进行存储。
因此,我们会将十进制值对一个大质数 modmod 进行取模。
此时:
1) 如果两个字符串的哈希值在取模后不相等,那么这两个字符串本身一定不相同;
2) 如果两个字符串的哈希值在取模后相等,并不能代表这两个字符串本身一定相同。
一般来说,我们选取一个大于字符集大小(即字符串中可能出现的字符种类的数目)的质数作为 base,再选取一个在字符串长度平方级别左右的质数作为 mod,产生哈希碰撞的概率就会很低。
PS:其实这里涉及到一定的概率。就是把字符串,按照方式转换为唯一的整数。
算法
一个字符串是回文串,当且仅当该字符串与它的反序相同。
因此,我们仍然暴力地枚举 s1 的结束位置,并计算 s1 与 s1 反序的哈希值。如果这两个哈希值相等,说明我们找到了一个 s 的前缀回文串。
在枚举 s1 的结束位置时,我们可以从小到大地进行枚举,这样就可以很容易地维护 s1 与 s1 反序的哈希值:
设当前枚举到的结束位置为 i,对应的 s1_i,其反序记为 ^s1_i。 我们可以通过递推的方式,在 O(1) 的时间,推送出哈希值。
hash(s1_i) = hash(s1_i-1) * base + ASCII(s[i]);
hash(^s1_i) = hash(^s1_i-1) + ASCII(s[i]) * base_i;
其中 ASCII(x) 表示字符 x 的 ASCII 码。
注意需要将结果对 mod 取模,避免溢出。
如果正反的哈希相同,则就是一个回文串。我们将最长的回文串作为最终的 s1。
java 实现
public String shortestPalindrome(String s) {
int base = 131, mod = 1000000007;
int left = 0, right = 0, mul = 1;
int best = -1;
for (int i = 0; i < s.length(); ++i) {
char c = s.charAt(i);
// 正序哈希
left = (int) (((long) left * base + c) % mod);
// 反序哈希
right = (int) ((right + (long) mul * c) % mod);
// 相同则为同一个
if (left == right) {
best = i;
}
mul = (int) ((long) mul * base % mod);
}
String add = (best == s.length() - 1 ? "" : s.substring(best + 1));
StringBuilder ans = new StringBuilder(add)
.reverse()
.append(s);
return ans.toString();
}
评价
这种算法实际上非常的巧妙,利用哈希值的计算可以递推,大大降低了耗时。实现方法本身也并不复杂。
当然,哈希计算存在一定的碰撞概率,可能存在误判。
用于这个测试场景是足够了,实际工业使用建议还是严谨一些,特别是在数据量特别大的情况下。
V4-KMP
思路
从 V2 可以看出,其实就是求 s 的「最长回文前缀」,然后在 rev_s 的后缀中砍掉这个回文,再加到 s 前面。
这个最长前缀是回文的,它翻转之后等于它自己,出现在 rev_s 的后缀,这不就是公共前后缀吗?
KMP 的 next 数组记录的就是一个字符串的每个位置上,最长公共前后缀的长度。公共前后缀指的是前后缀相同。
因此,我们 “制造” 出公共前后缀,去套 KMP。
s:abab,则 s + ‘#’ + rev_s,得到 str :abab#baba。
求出 next 数组,最后一项就是 str 的最长公共前后缀的长度,即 s 的最长回文前缀的长度。
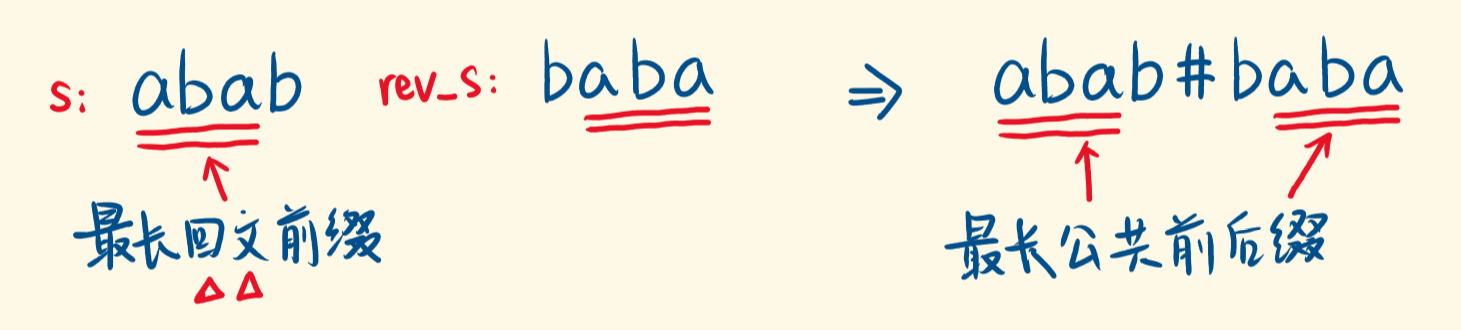
如果不加 #,’aaa’+’aaa’得到’aaaaaa’,求出的最长公共前后缀是 6,但其实想要的是 3。
java 实现
public String shortestPalindrome(String s) {
if(s.length()<=1){
return s;
}
// 翻转相加
String rev = new StringBuffer(s).reverse().toString();
rev = s + "#" + rev;
// 计算 kmp next 数组
int index = kmp(rev);
// 截取拼接
return new StringBuffer(s.substring(index+1)).reverse() +s;
}
/**
* 计算 kmp 的 next 数组,这里只需要返回最后一个值即可。
*
* @param pattern
* @return
*/
private int kmp(String pattern) {
int n = pattern.length();
int[] next = new int[n];
next[0]=-1;
int j = -1;
for(int i=1; i<n; i++){
while(j != -1 && pattern.charAt(i)!= pattern.charAt(j+1)) {
j=next[j];
}
if(pattern.charAt(i)== pattern.charAt(j+1)) {
j+=1;
}
next[i]=j;
}
return next[n-1];
}
点评
实际上这需要对 kmp 比较熟悉,特别是对 next 的数组理解比较深入。
一般还是很难想到的,反而是下面的算法应该被自然想到。
V5-Manacher Algorithm 马拉车算法
算法
马拉车算法 Manacher‘s Algorithm 是用来查找一个字符串的最长回文子串的线性方法,由一个叫Manacher的人在1975年发明的,这个方法的最大贡献是在于将时间复杂度提升到了线性。
思路
前面的 V2/V3,对于问题的核心都是从头开始寻找最长的回文串。
我们通过马拉车算法,把这个复杂度降低到线性。
PS: 这个算法相对比较难记忆,但是模板其实是固定的。
java 实现
class Solution {
/**
* 马拉车算法
*
* https://leetcode.cn/problems/shortest-palindrome/solution/can-kao-zuo-shen-manacherde-dai-ma-jie-f-y2ba/
* @param source
* @return
*/
public String shortestPalindrome(String source) {
if (source.length() == 0) {
return source;
}
StringBuilder sb = new StringBuilder(source).reverse();
String s = sb.toString();
char[] str = manacherString(s);
int[] pArr = new int[str.length];
int R = -1;
int C = -1;
for (int i = 0; i < str.length; i++) {
int i1 = C - (i - C);
// i' 的回文区域在L...R边界上的话, pArr[i1] 和 R-i 是相等的
pArr[i] = (i < R) ? Math.min(pArr[i1], R - i) : 1;
while (i + pArr[i] < str.length && i - pArr[i] > -1) {
if (str[i + pArr[i]] == str[i - pArr[i]]) {
pArr[i]++;
} else {
break;
}
}
if (i + pArr[i] > R) {
R = i + pArr[i];
C = i;
}
// 某个字符使 R 达到了边界
if (R == str.length) {
break;
}
}
// 从当前的中心点的 L 往前遍历,都加入到后面去
// L 为 -1 则说明 source 原本就是个回文
int L = C - (R - C);
// 因为是加工过的字符串,要除二
L = L == -1 ? L : L / 2;
int len = source.length() - 1;
for (int i = L; i >= 0; i--) {
sb.append(source.charAt(len - i));
}
// res 不用再 reverse 回去了,因为已经处理成回文了
return sb.toString();
}
private char[] manacherString(String s) {
char[] chars = s.toCharArray();
char[] res = new char[s.length() * 2 + 1];
for (int i = 0; i < res.length; i++) {
res[i] = (i % 2 == 0) ? '#' : chars[i / 2];
}
return res;
}
}
小结
一道非常好的题目,好的测试 case。
可以让解题者不是止步于前两种解法而自满,又有多种解法。
参考资料
https://leetcode.cn/problems/shortest-palindrome/solution/manacherqiu-zui-chang-hui-wen-qian-zhui-c17qo/
https://leetcode.cn/problems/shortest-palindrome/solution/manacher-by-emperoroffailure-vj9e/
https://leetcode.cn/problems/shortest-palindrome/solution/java-kmp-by-lyl-36-zrfx/
https://zhuanlan.zhihu.com/p/79887898
https://leetcode.cn/problems/shortest-palindrome/solution/214-zui-duan-hui-wen-chuan-zi-fu-chuan-h-zseq/
https://leetcode.cn/problems/shortest-palindrome/
https://leetcode.cn/problems/shortest-palindrome/solution/zui-duan-hui-wen-chuan-by-leetcode-solution/
https://leetcode.cn/problems/shortest-palindrome/solution/shou-hua-tu-jie-cong-jian-dan-de-bao-li-fa-xiang-d/
https://leetcode.cn/problems/shortest-palindrome/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by–44/
https://leetcode.cn/problems/shortest-palindrome/solution/by-flix-be4y/
