相关分析方法
一、什么是相关分析方法?
1、定义:研究两种或两种以上数据有什么关系。
如:
身高和体重有什么关系?工作压力和冠心病发病率(猝死)有什么关系?
二、相关分析方法有什么用?
1、在研究两种或两种以上的数据之间有什么关系,或者某件事受到其他因素导致产生什么样的影响。
A和B有什么关系?A 对B有什么影响?
2、有助于扩大思路,从一个数据分析思路变成两个数据分析思路甚至更多
例如:销售量下降,可以从产品价格,产品质量,售后服务等方面入手分析
3、在工作中,相关分析方法对于业务上能够更通俗易懂,有数据支持和加持,双方之间的沟通更便利。
4、深入分析:其他分析方法+相关分析方法
三、相关分析方法如何用?
1、散点图
① 定义:由一些散乱的点组成的图表,这些点在哪个位置,是由其X值和Y值确定的。
所以也叫做XY散点图。
② 作用:
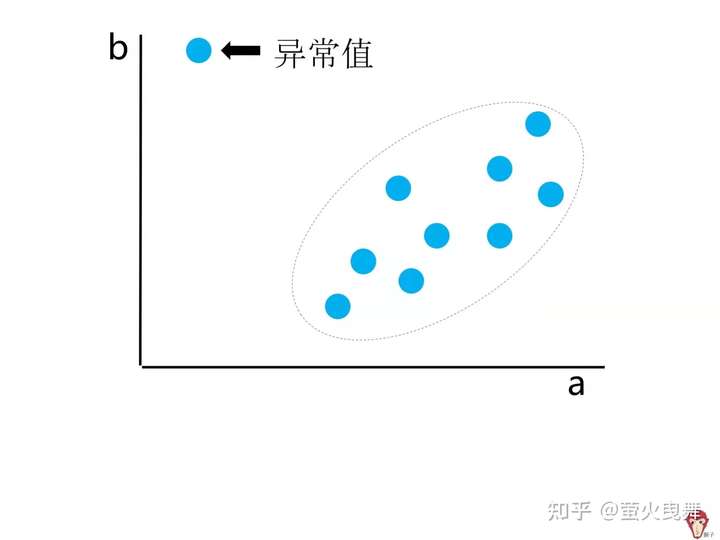
作用一:可以展示数据的分布和聚合情况作用二:得到趋势线公式作用三:辅助制图(用散点图的误差线辅助制图)作用四:通过散点图发现哪些属于异常值和非异常值。(如图)
协方差级协方差矩阵
正相关
负相关
不相关
ps: 对应的计算公式。
3、相关系数(R)
①定义:研究变量之间线性相关程度的量
②作用:
作用1:指数值的大小表示两者之间的相关程度
通过分析,我们发现跟复购率相关度最高的因素是助教的答疑效果,优先提高助教的答疑服务,可以显著提高产品的复购率。
R_xy = S_xy / (S_x * S_y)
其中rxy表示样本相关系数,Sxy表示样本协方差,Sx表示X的样本标准差,Sy表示y的样本标准差。下面分别是Sxy协方差和Sx和Sy标准差的计算公式。由于是样本协方差和样本标准差,因此分母使用的是n-1。
相关系数的优点是可以通过数字对变量的关系进行度量,并且带有方向性,1表示正相关,-1表示负相关,可以对变量关系的强弱进行度量,越靠近0相关性越弱。
缺点是无法利用这种关系对数据进行预测,简单的说就是没有对变量间的关系进行提炼和固化,形成模型。要利用变量间的关系进行预测,需要使用到下一种相关分析方法,回归分析。
4、一元回归及多元回归
第四种相关分析方法是回归分析。
回归分析(regression analysis)是确定两组或两组以上变量间关系的统计方法。回归分析按照变量的数量分为一元回归和多元回归。两个变量使用一元回归,两个以上变量使用多元回归。
进行回归分析之前有两个准备工作,第一确定变量的数量。第二确定自变量和因变量。我们的数据中只包含广告曝光量和费用成本两个变量,因此使用一元回归。根据经验广告曝光量是随着费用成本的变化而改变的,因此将费用成本设置为自变量x,广告曝光量设置为因变量y。
以下是一元回归方程,其中y表示广告曝光量,x表示费用成本。b0为方程的截距,b1为斜率,同时也表示了两个变量间的关系。我们的目标就是b0和b1的值,知道了这两个值也就知道了变量间的关系。并且可以通过这个关系在已知成本费用的情况下预测广告曝光量。
这是b1的计算公式,我们通过已知的费用成本x和广告曝光量y来计算b1的值。
以下是通过最小二乘法计算b1值的具体计算过程和结果,经计算,b1的值为5.84。同时我们也获得了自变量和因变量的均值。
通过这三个值可以计算出b0的值。
以下是b0的计算公式,在已知b1和自变量与因变量均值的情况下,b0的值很容易计算。
将自变量和因变量的均值以及斜率b1代入到公式中,求出一元回归方程截距b0的值为374。这里b1我们保留两位小数,取值5.84。
在实际的工作中不需要进行如此繁琐的计算,Excel可以帮我们自动完成并给出结果。
在Excel中使用数据分析中的回归功能,输入自变量和因变量的范围后可以自动获得b0(Intercept)的值362.15和b1的值5.84。这里的b0和之前手动计算获得的值有一些差异,因为前面用于计算的b1值只保留了两位小数。
这里还要单独说明下R Square的值0.87。这个值叫做判定系数,用来度量回归方程的拟合优度。
这个值越大,说明回归方程越有意义,自变量对因变量的解释度越高。
将截距b0和斜率b1代入到一元回归方程中就获得了自变量与因变量的关系。费用成本每增加1元,广告曝光量会增加379.84次。
通过这个关系我们可以根据成本预测广告曝光量数据。也可以根据转化所需的广告曝光量来反推投入的费用成本。
获得这个方程还有一个更简单的方法,就是在Excel中对自变量和因变量生成散点图,然后选择添加趋势线,在添加趋势线的菜单中选中显示公式和显示R平方值即可。
y = 374 + 5.84x
以上介绍的是两个变量的一元回归方法,如果有两个以上的变量使用Excel中的回归分析,选中相应的自变量和因变量范围即可。
下面是多元回归方程。
y = b0 + b1x1 + b2x2 + .... + bnxn
5、信息熵及互信息
最后一种相关分析方法是信息熵与互信息。前面我们一直在围绕消费成本和广告曝光量两组数据展开分析。
实际工作中影响最终效果的因素可能有很多,并且不一定都是数值形式。比如我们站在更高的维度来看之前的数据。
广告曝光量只是一个过程指标,最终要分析和关注的是用户是否购买的状态。而影响这个结果的因素也不仅仅是消费成本或其他数值化指标。可能是一些特征值。
例如用户所在的城市,用户的性别,年龄区间分布,以及是否第一次到访网站等等。这些都不能通过数字进行度量。
度量这些文本特征值之间相关关系的方法就是互信息。通过这种方法我们可以发现哪一类特征与最终的结果关系密切。
下面是我们模拟的一些用户特征和数据。在这些数据中我们忽略之前的消费成本和广告曝光量数据,只关注特征与状态的关系。
对于信息熵和互信息具体的计算过程请参考文章《决策树分类和预测算法的原理及实现》,这里直接给出每个特征的互信息值以及排名结果。
经过计算城市与购买状态的相关性最高,所在城市为北京的用户购买率较高。
到此为止5种相关分析方法都已介绍完,每种方法各有特点。
其中图表方法最为直观,相关系数方法可以看到变量间两两的相关性,回归方程可以对相关关系进行提炼,并生成模型用于预测,互信息可以对文本类特征间的相关关系进行度量。
四、注意事项有哪些?
1、相关关系不等于因果关系。
例如: 暴饮暴食和肥胖属于因果关系A和B呈现正相关关系,A越大,则B越大,但是不能反过来
2、如何区分相关关系和因果关系?
单变量控制方法:控制其他因素不变,只改变其中一个因素,观察这个因素对实验结果的影响。
如:公鸡打鸣和太阳升起。太阳升起不会因为公鸡是否打鸣而影响,所以这两者就属于相关关系。
参考资料
https://zhuanlan.zhihu.com/p/415840276
https://baijiahao.baidu.com/s?id=1716142810265383020&wfr=spider&for=pc
https://blog.csdn.net/mituan1234567/article/details/53005718
