数组
大家好,我是老马。
今天我们一起来学习一下数组这种数据结构。
主要知识
数组需要拆分下面几个部分:
-
理论介绍
-
源码分析
-
数据结构实现?
-
题目练习(按照算法思想分类)
-
梳理对应的 sdk 包
-
应用实战
因为这个是 leetcode 系列,所以重点是 4、5(对4再一次总结)。
为了照顾没有基础的小伙伴,会简单介绍一下1的基础理论。
简单介绍1,重点为4。其他不是本系列的重点。
数据结构篇
https://leetcode.cn/studyplan/top-100-liked/
LC160. 相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。
如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal - 相交的起始节点的值。如果不存在相交节点,这一值为 0 listA - 第一个链表 listB - 第二个链表 skipA - 在 listA 中(从头节点开始)跳到交叉节点的节点数 skipB - 在 listB 中(从头节点开始)跳到交叉节点的节点数 评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:

输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3 输出:Intersected at ‘8’ 解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。 在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。 — 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例 2:

输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出:Intersected at ‘2’ 解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。 在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
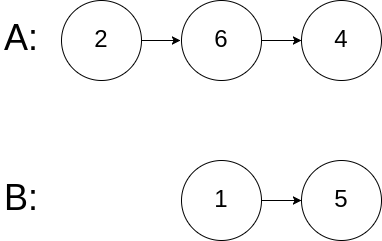
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出:No intersection 解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。 由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。 这两个链表不相交,因此返回 null 。
提示:
listA 中节点数目为 m listB 中节点数目为 n 1 <= m, n <= 3 * 10^4 1 <= Node.val <= 10^5 0 <= skipA <= m 0 <= skipB <= n 如果 listA 和 listB 没有交点,intersectVal 为 0 如果 listA 和 listB 有交点,intersectVal == listA[skipA] == listB[skipB]
进阶:你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案?
v1-Hash
思路
这一题,最核心的是判断两个节点是否相交。
也就是 nodeA==nodeB
最简单的方式使用 Hash 存储一个链表节点,另一个遍历时判断是否存在相同的节点即可。
实现
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
Set<ListNode> set = new HashSet<>();
while (headA != null) {
set.add(headA);
headA = headA.next;
}
// 找到 b 中重复的点
while (headB != null) {
if(set.contains(headB)) {
return headB;
}
headB = headB.next;
}
return null;
}
效果
6ms 击败 22.90%
复杂度
TC O(m+n)
SC O(m)
反思
也就是空间复杂度不满足条件。
如何降低空间?
v2-长度对齐
思路
因为相交的点,从交点之后,后面的长度是一样的。
所以,可以先请求长度 lenA, lenB。让长的先走 abs(lenA-lenB) 步骤,然后一起判断共同节点。
主要注意的是,如果用方法,java 方法是值传递。
实现
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
// 注意:java 方法是值传递
int lenA = getLen(headA);
int lenB = getLen(headB);
// 长的先走
int diff = Math.abs(lenA-lenB);
if(lenA > lenB) {
headA = jumpDiffer(headA, diff);
} else if(lenA < lenB) {
headB = jumpDiffer(headB, diff);
}
// 一起走 找到共同的节点
while (headA != null && headB != null) {
if(headA == headB) {
return headB;
}
headA = headA.next;
headB = headB.next;
}
// NOT FOUND
return null;
}
private int getLen(ListNode node) {
int len = 0;
while (node != null) {
node = node.next;
len++;
}
return len;
}
// java 是值传递,需要返回
private ListNode jumpDiffer(ListNode node, int differ) {
while (differ > 0) {
node = node.next;
differ--;
}
return node;
}
效果
1ms 击败 99.92%
TC: O(m + n)
SC: O(1)
v3-双指针
思路
这个技巧性比较强
原理核心在于:让两个指针走过相同的路径长度,从而实现对齐。
🧠 解法核心思想:
假设:
- 链表A长度为
a + c,其中a是非公共部分,c是公共部分; - 链表B长度为
b + c,其中b是非公共部分,c是公共部分; - 如果两个链表有公共部分,那这个公共部分的长度
c是相同的,且节点地址相同。
目标:让两个指针同时到达交点 c 的起始处。
🚀 解法步骤:
- 定义两个指针
pA和pB,分别从链表 A 和 B 的头部出发。 -
每轮遍历向后移动一步:
- 如果走到末尾(null),就跳到另一个链表的头继续走。
-
最终:
- 要么在某个节点相遇(就是交点),
- 要么都走完变为 null(说明无交点)。
✅ 为什么这个做法有效?
因为:
- 指针 A 实际上走了路径:
a + c + b - 指针 B 实际上走了路径:
b + c + a
两者总共走了 a + b + c,所以只要有交点,他们最终会同时走到 c 的起点。
若无交点,则两者都走到 null(末尾),同样能退出。
例子
链表 A: a1 → a2 → a3 → c1 → c2 → c3
链表 B: b1 → b2 → c1 → c2 → c3
↑———— 公共部分 c ————↑
pA走路径:a1 → a2 → a3 → c1 → c2 → c3 → b1 → b2 → c1 → ...
pB走路径:b1 → b2 → c1 → c2 → c3 → a1 → a2 → a3 → c1 → ...
走了 a + b + c 后同步到达 c1!
实现
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode pA = headA;
ListNode pB = headB;
while (pA != pB) {
pA = (pA == null) ? headB : pA.next;
pB = (pB == null) ? headA : pB.next;
}
return pA;
}
}
效果
1ms 99.92%
在线可视化
数据结构
通用基础
链表
树
哈希表
stack 栈
graph 图
heap 堆
ordered set 有序集合
queue 队列
进阶
并查集
字典树
线段树
树状数组
后缀数组
