31. 下一个排列
题目
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。
更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。
如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
例子
示例 1:
输入:nums = [1,2,3] 输出:[1,3,2]
示例 2:
输入:nums = [3,2,1] 输出:[1,2,3]
示例 3:
输入:nums = [1,1,5] 输出:[1,5,1]
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 100
思路
-
如何判断有木有下一个呢?只要存在a[i-1] < a[i]的升序结构,就有,而且我们应该从右往左找
-
当发现a[i-1] < a[i]的结构时,从在[i, ∞]中找到最接近a[i-1]并且又大于a[i-1]的数字,由于降序,从右往左遍历即可得到k
然后交换a[i-1]与a[k],然后对[i, ∞]排序即可,排序只需要首尾不停交换即可,因为已经是降序 上面说的很抽象,还是需要拿一些例子思考才行。
以排列 [4,5,2,6,3,1] 为例:
我们能找到的符合条件的一对「较小数」与「较大数」的组合为 22 与 33,满足「较小数」尽量靠右,而「较大数」尽可能小。
当我们完成交换后排列变为 [4,5,3,6,2,1],此时我们可以重排「较小数」右边的序列,序列变为 [4,5,3,1,2,6]。
算法
具体地,我们这样描述该算法,对于长度为 n 的排列 a:
1) 首先从后向前查找第一个顺序对 (i,i+1) ,满足 a[i] < a[i+1]。这样「较小数」即为 a[i]。此时 [i+1,n) 必然是下降序列。
2) 如果找到了顺序对,那么在区间 [i+1,n) 中从后向前查找第一个元素 jj 满足 a[i] < a[j]。这样「较大数」即为 a[j]a[j]。
3) 交换 a[i] 与 a[j],此时可以证明区间 [i+1,n) 必为降序。我们可以直接使用双指针反转区间 [i+1,n) 使其变为升序,而无需对该区间进行排序。
如果在步骤 1 找不到顺序对,说明当前序列已经是一个降序序列,即最大的序列,我们直接跳过步骤 2 执行步骤 3,即可得到最小的升序序列。
java 实现
class Solution {
public void nextPermutation(int[] nums) {
int i = nums.length - 2;
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--;
}
if (i >= 0) {
int j = nums.length - 1;
while (j >= 0 && nums[i] >= nums[j]) {
j--;
}
swap(nums, i, j);
}
reverse(nums, i + 1);
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
public void reverse(int[] nums, int start) {
int left = start, right = nums.length - 1;
while (left < right) {
swap(nums, left, right);
left++;
right--;
}
}
}
46. 全排列 permutations
题目
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列。
你可以 按任意顺序 返回答案。
例子
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
```
### 提示:
1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同
## 思路
针对这种全排列问题,直接使用回溯解决即可。
> [回溯算法-backtrack](https://houbb.github.io/2020/01/23/data-struct-learn-07-base-backtracking)
## java 实现
```java
public List<List<Integer>> permute(int[] nums) {
// 这个个数实际上可以预测:就是 nums ! 阶乘。
// 实测优化效果不明显
final int len = nums.length;
List<List<Integer>> results = new ArrayList<>();
// 避免扩容
List<Integer> tempList = new ArrayList<>(len);
backtrack(results, tempList, nums);
return results;
}
private void backtrack(List<List<Integer>> results, List<Integer> tempList, int[] nums) {
// 什么时候停止
final int len = nums.length;
// 满足条件
if(tempList.size() == len) {
results.add(new ArrayList<>(tempList));
} else {
// 回溯
for (int current : nums) {
// 元素不能重复
if (tempList.contains(current)) {
continue;
}
tempList.add(current);
// 下一个元素
backtrack(results, tempList, nums);
// 回溯
tempList.remove(tempList.size() - 1);
}
}
}
47. 全排列 II permutations-ii
题目
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
例子
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
```
提示:
1 <= nums.length <= 8
-10 <= nums[i] <= 10
## V1-复用 46
### 思路
这一题和 46 的区别,就是输入的整数可能存在重复。
整体实现回溯的时候,把原来的 `tempList.contains(current)` 判断元素是否重复,替换为 visit[] 数组。因为可能存在相同的元素。
我们整体逻辑不变,在最后返回的时候统一做一个过滤。
### java 实现
```java
class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
// 这个个数实际上可以预测:就是 nums ! 阶乘。
// 实测优化效果不明显
final int len = nums.length;
boolean[] used = new boolean[len];
List<List<Integer>> results = new ArrayList<>();
// 避免扩容
List<Integer> tempList = new ArrayList<>(len);
backtrack(results, tempList, nums, used);
// 过滤重复的值
return filter(results);
}
private void backtrack(List<List<Integer>> results, List<Integer> tempList, int[] nums,
boolean[] used) {
// 什么时候停止
final int len = nums.length;
if(tempList.size() == len) {
results.add(new ArrayList<>(tempList));
} else {
// 回溯
for (int i = 0; i < nums.length; i++) {
// 元素不能重复使用
if (used[i]) {
continue;
}
tempList.add(nums[i]);
used[i] = true;
// 下一个元素
backtrack(results, tempList, nums, used);
// 回溯
tempList.remove(tempList.size() - 1);
used[i] = false;
}
}
}
private List<List<Integer>> filter(List<List<Integer>> all) {
List<List<Integer>> results = new ArrayList<>();
for(List<Integer> list : all) {
if(!results.contains(list)) {
results.add(list);
}
}
return results;
}
}
效果
Runtime: 857 ms, faster than 5.26% of Java online submissions for Substring with Concatenation of All Words.
Memory Usage: 47.4 MB, less than 22.52% of Java online submissions for Substring with Concatenation of All Words.
看的出来,虽然简单粗暴,但是性能确实令人担忧。
主要是回溯的时候没有对重复元素进行剪枝,比较慢。
V2-剪枝
思路
针对上面的算法,我们可以略微改进。
首先对数组进行排序,这样更好的判断相邻数据的大小。
需要额外的一个过滤条件:
// 如果有重复的元素,就会导致重复。(需要数组进行排序)
// 1_a 1_b 2 第一次 1_a 1_b 2
// 如果出现 1_b 1_a 2 实际上就重复了。(需要跳过的 case)
if(i > 0 && nums[i] == nums[i-1] && !used[i-1]) {
continue;
}
如果当前位置数字和上一个相同,且上一个没被使用,则跳过。因为这个数已经回溯过一次了。
这样最后也不需要进行过滤,整体的结果不存在重复数据。
java 实现
class Solution {
/**
* 解题思路:回溯算法
*
* 【优化思路】
* 避免数组扩容
*
* @param nums 数字
* @return 结果
* @since v46
*/
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
// 这个个数实际上可以预测:就是 nums ! 阶乘。
// 实测优化效果不明显
final int len = nums.length;
List<List<Integer>> results = new ArrayList<>();
boolean[] used = new boolean[len];
// 避免扩容
List<Integer> tempList = new ArrayList<>(len);
backtrack(results, tempList, nums, used);
return results;
}
private void backtrack(List<List<Integer>> results, List<Integer> tempList, int[] nums,
boolean[] used) {
// 什么时候停止
final int len = nums.length;
if(tempList.size() == len) {
results.add(new ArrayList<>(tempList));
} else {
// 回溯
for (int i = 0; i < len; i++) {
// 已经被使用的,不能重复使用。
// 如果没有重复的元素,这样就要够了
if(used[i]) {
continue;
}
// 如果有重复的元素,就会导致重复。(需要数组进行排序)
// 1_a 1_b 2 第一次 1_a 1_b 2
// 如果出现 1_b 1_a 2 实际上就重复了。(需要跳过的 case)
if(i > 0 && nums[i] == nums[i-1] && !used[i-1]) {
continue;
}
int current = nums[i];
tempList.add(current);
used[i] = true;
// 下一个元素
backtrack(results, tempList, nums, used);
// 回溯
used[i] = false;
tempList.remove(tempList.size() - 1);
}
}
}
}
效果
Runtime: 1 ms, faster than 100% of Java online submissions for Substring with Concatenation of All Words.
Memory Usage: 39.4 MB, less than 100% of Java online submissions for Substring with Concatenation of All Words.
效果拔群,可见在回溯中剪枝的重要性。
60. 排列序列 permutation sequence
题目
给出集合 [1,2,3,…,n],其所有元素共有 n! 种排列。
按大小顺序列出所有排列情况,并一一标记,当 n = 3 时, 所有排列如下:
"123"
"132"
"213"
"231"
"312"
"321"
给定 n 和 k,返回第 k 个排列。
例子
示例 1:
输入:n = 3, k = 3
输出:"213"
示例 2:
输入:n = 4, k = 9
输出:"2314"
示例 3:
输入:n = 3, k = 1
输出:"123"
提示:
1 <= n <= 9
1 <= k <= n!
v1-基本方式
思路
给出集合 [1,2,3,…,n],其所有元素共有 n! 种排列。
求排列其实是 T46 的子集,我们把所有的结果处理放在列表中,达到 k 的时候就结束。
java 实现
public String getPermutation(int n, int k) {
List<List<Integer>> all = new ArrayList<>();
List<Integer> tempList = new ArrayList<>();
backtrack(all, tempList, n, k, 1);
// 返回列表中的最后一个。
List<Integer> integers = all.get(k-1);
StringBuilder stringBuilder = new StringBuilder();
for(Integer i : integers) {
stringBuilder.append(i);
}
return stringBuilder.toString();
}
// 如何可以簡化這個操作呢?
// 其實我們只關心第 K 個元素
private void backtrack(List<List<Integer>> all, List<Integer> tempList,
int n, int k, int start) {
if(tempList.size() == n) {
// 满了
all.add(new ArrayList<>(tempList));
// 如果大小已经够了,直接剪枝
if(all.size() >= k) {
return;
}
}
for(int i = 1; i <= n; i++) {
// 跳过重复的元素
if(tempList.contains(i)) {
continue;
}
tempList.add(i);
// 下一个元素
backtrack(all, tempList, n, k, start+1);
// 移除,回溯
tempList.remove(tempList.size()-1);
}
}
不过这样,会直接超时。
V2-回溯剪枝
思路
思路分析:容易想到,使用同「力扣」第 46 题: 全排列 的回溯搜索算法,依次得到全排列,输出第 k 个全排列即可。
事实上,我们不必求出所有的全排列。
基于以下几点考虑:
所求排列 一定在叶子结点处得到,进入每一个分支,可以根据已经选定的数的个数,进而计算还未选定的数的个数,然后计算阶乘,就知道这一个分支的 叶子结点 的个数:
如果 k 大于这一个分支将要产生的叶子结点数,直接跳过这个分支,这个操作叫「剪枝」;
如果 k 小于等于这一个分支将要产生的叶子结点数,那说明所求的全排列一定在这一个分支将要产生的叶子结点里,需要递归求解。
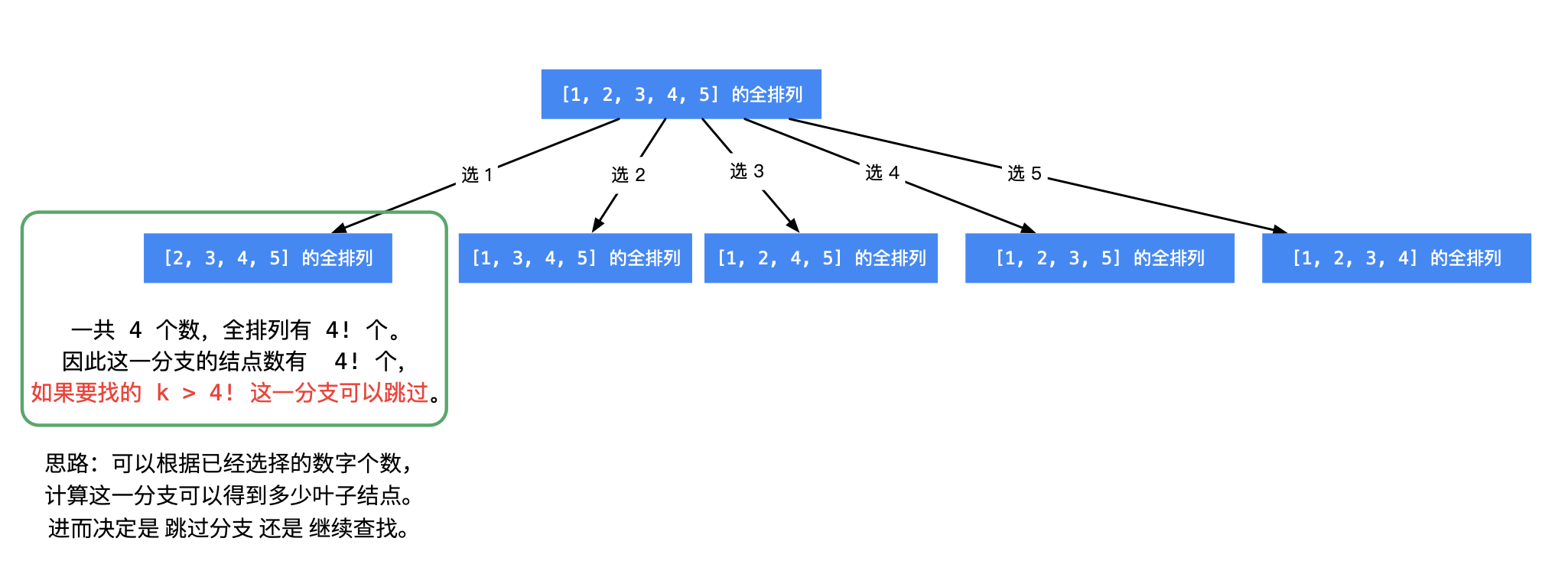
阶乘
阶乘算法,直接使用递推公式,初始化:
/**
* 计算阶乘数组
*
* @param n
*/
private void calculateFactorial(int n) {
factorial = new int[n + 1];
factorial[0] = 1;
for (int i = 1; i <= n; i++) {
factorial[i] = factorial[i - 1] * i;
}
}
java 实现
整体实现和 T46 类似,不过加入了剪枝。
import java.util.Arrays;
public class Solution {
/**
* 记录数字是否使用过
*/
private boolean[] used;
/**
* 阶乘数组
*/
private int[] factorial;
private int n;
private int k;
public String getPermutation(int n, int k) {
this.n = n;
this.k = k;
calculateFactorial(n);
// 查找全排列需要的布尔数组
used = new boolean[n + 1];
Arrays.fill(used, false);
StringBuilder path = new StringBuilder();
dfs(0, path);
return path.toString();
}
/**
* @param index 在这一步之前已经选择了几个数字,其值恰好等于这一步需要确定的下标位置
* @param path
*/
private void dfs(int index, StringBuilder path) {
if (index == n) {
return;
}
// 计算还未确定的数字的全排列的个数,第 1 次进入的时候是 n - 1
// 直接根据计算好的排列,计算当前的 count
int cnt = factorial[n - 1 - index];
for (int i = 1; i <= n; i++) {
if (used[i]) {
continue;
}
if (cnt < k) {
k -= cnt;
continue;
}
path.append(i);
used[i] = true;
dfs(index + 1, path);
// 注意 1:不可以回溯(重置变量),算法设计是「一下子来到叶子结点」,没有回头的过程
// 注意 2:这里要加 return,后面的数没有必要遍历去尝试了
return;
}
}
/**
* 计算阶乘数组
*
* @param n
*/
private void calculateFactorial(int n) {
factorial = new int[n + 1];
factorial[0] = 1;
for (int i = 1; i <= n; i++) {
factorial[i] = factorial[i - 1] * i;
}
}
}
这种算法真的很强,剪枝的技巧很难想到。
复杂度分析
时间复杂度:O(N^2),这里 N 是数组的长度;
空间复杂度:O(N)。
V3-有序数组(链表)模拟
思路
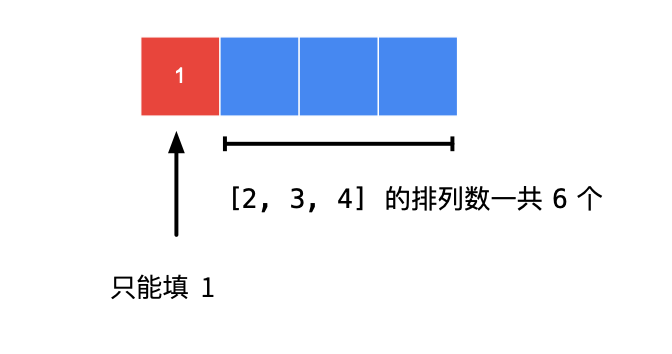
以 n = 4,k = 6,为例,现在确定第 11 个数字填啥。
如果第 k 个数恰好是后面的数字个数的阶乘,那么第 11 个数字就只能填最小的 11。
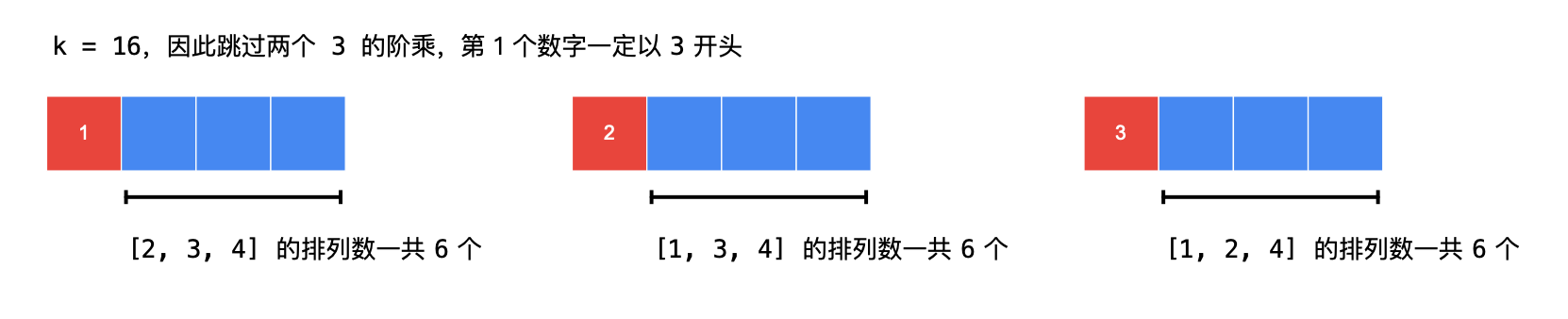
如果 n = 4,k = 16,现在确定第 11 个数字填啥。如果 k > 后面的数字个数的阶乘。
数一数,可以跳过几个阶乘数。
其实这个思路很像方法一的「剪枝」,只不过方法一就减法,方法二用除法。
事实上,方法二要维护数组的有序性,所以时间复杂度不变。
根据以上思路,设计算法流程如下
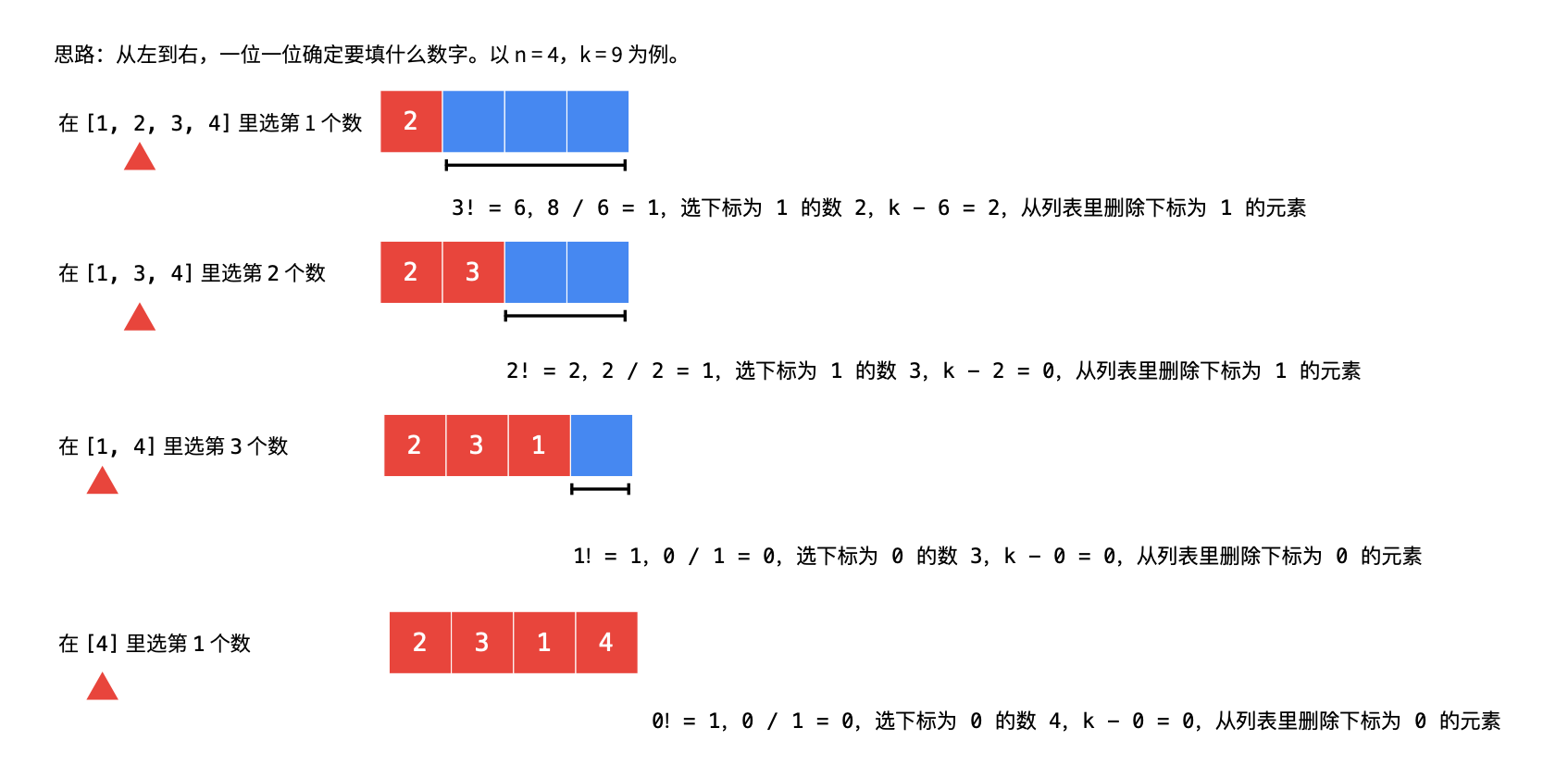
算法
1) 把候选数放在一个 有序列表 里,从左到右根据「剩下的数的阶乘数」确定每一位填谁,公式 k / (后面几位的阶乘数) 的值 恰好等于候选数组的下标; 选出一个数以后,k 就需要减去相应跳过的阶乘数的倍数;
2) 已经填好的数需要从候选列表里删除,注意保持列表的有序性(因为排列的定义是按照字典序);
3) 由于这里考虑的是下标,第 k 个数,下标为 k - 1,一开始的时候,k–。
4) 每次选出一个数,就将这个数从列表里面拿出。这个列表需要支持频繁的删除操作,因此使用双链表。在 Java 中 LinkedList 就是使用双链表实现的。
例 2:
java 实现
import java.util.LinkedList;
import java.util.List;
public class Solution {
public String getPermutation(int n, int k) {
// 注意:相当于在 n 个数字的全排列中找到下标为 k - 1 的那个数,因此 k 先减 1
k --;
int[] factorial = new int[n];
factorial[0] = 1;
// 先算出所有的阶乘值
for (int i = 1; i < n; i++) {
factorial[i] = factorial[i - 1] * i;
}
// 这里使用数组或者链表都行
List<Integer> nums = new LinkedList<>();
for (int i = 1; i <= n; i++) {
nums.add(i);
}
StringBuilder stringBuilder = new StringBuilder();
// i 表示剩余的数字个数,初始化为 n - 1
for (int i = n - 1; i >= 0; i--) {
int index = k / factorial[i] ;
stringBuilder.append(nums.remove(index));
k -= index * factorial[i];
}
return stringBuilder.toString();
}
}
复杂度分析
时间复杂度:O(N^2),这里 N 是数组的长度;
空间复杂度:O(N)。
开源地址
为了便于大家学习,所有实现均已开源。欢迎 fork + star~
参考资料
https://leetcode.cn/problems/next-permutation/solution/xia-yi-ge-pai-lie-by-leetcode-solution/
https://leetcode.cn/problems/permutations/
https://leetcode.cn/problems/permutations-ii/
https://leetcode.cn/problems/permutation-sequence/solution/di-kge-pai-lie-by-leetcode-solution/
https://leetcode.cn/problems/permutation-sequence/solution/hui-su-jian-zhi-python-dai-ma-java-dai-ma-by-liwei/
