33. 搜索旋转排序数组 Search in Rotated Sorted Array
题目
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。
例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
例子
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
```
提示:
1 <= nums.length <= 5000
-10^4 <= nums[i] <= 10^4
nums 中的每个值都 独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-10^4 <= target <= 10^4
## v1-二分法青春版
### 思路
[0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
我们首先应该找到这个数组旋转的位置 k,然后把数组分为 2 个部分,这样依然是有序的。
然后采用分别二分法查询即可。
### 实现
```java
/**
* Input: nums = [4,5,6,7,0,1,2], target = 0
* Output: 4
* @param nums
* @param target
* @return
*/
public int search(int[] nums, int target) {
// 没有旋转,或者全部旋转
int randomK = getRandomK(nums);
if(-1 == randomK) {
return binarySearch(nums, target, 0, nums.length-1);
}
// 将数组拆成2个部分
// 4 5 6 7 0 1 2 => [4 5 6 7] [0 1 2]
// 3 1 ==> [3] [1]
int leftIndex = binarySearch(nums, target, 0, randomK);
if(leftIndex != -1) {
return leftIndex;
}
// 右边寻找
int rightIndex = binarySearch(nums, target, randomK+1, nums.length-1);
if(rightIndex != -1) {
return rightIndex;
}
// 如果不存在
return -1;
}
/**
* 获取随机数
*
* 寻找 k > k+i 的位置
*
* [4,5,6,7,0,1,2]
* @param nums 数组
* @return 变化的长度
* @since v33
*/
private int getRandomK(final int[] nums) {
for(int i = 0; i < nums.length-1; i++) {
if(nums[i] > nums[i+1]) {
return i;
}
}
// 根据顺序找到即可
return -1;
}
/**
* 二分查询
* <p>
* 备注:ASC
*
* @param nums 原始数组
* @param target 目标值
* @return 结果
* @since v33
*/
private static int binarySearch(int[] nums, int target, int low, int high) {
while (low <= high) {
int mid = (high+low)/2;
int midVal = nums[mid];
// 刚好相等
if (target == midVal) {
return mid;
} else if (target > midVal) {
// 当前信息偏小
low = mid+1;
} else {
// 数据偏大
high = mid-1;
}
}
//NOT FOUND
return -1;
}
评价
这个算法思路没有问题。
但是在计算 random-k 的时候,最差的复杂度为 O(N)。所以值得进一步优化。
v2-二分法
思路
对于有序数组,可以使用二分查找的方法查找元素。
但是这道题中,数组本身不是有序的,进行旋转后只保证了数组的局部是有序的,这还能进行二分查找吗?答案是可以的。
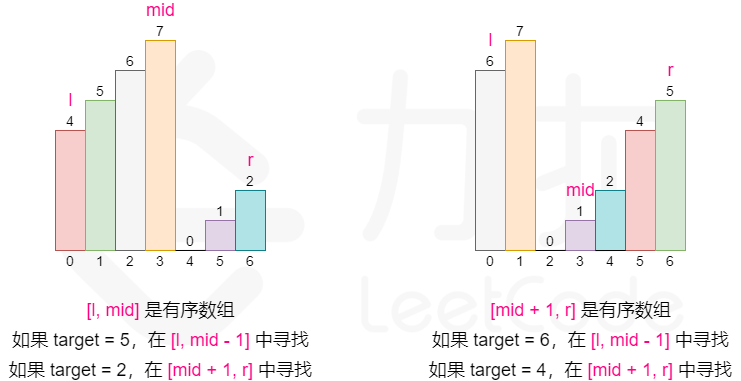
可以发现的是,我们将数组从中间分开成左右两部分的时候,一定有一部分的数组是有序的。
拿示例来看,我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分,其中左边 [4, 5, 6] 这个部分的数组是有序的,其他也是如此。
这启示我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的,并根据有序的那个部分确定我们该如何改变二分查找的上下界,因为我们能够根据有序的那部分判断出 target 在不在这个部分:
如果 [l, mid - 1] 是有序数组,且 target 的大小满足 [nums[l], nums[mid]],则我们应该将搜索范围缩小至 [l, mid-1],否则在 [mid + 1, r] 中寻找。
如果 [mid, r] 是有序数组,且 target 的大小满足 [nums[mid+1], nums[r]],则我们应该将搜索范围缩小至 [mid + 1, r],否则在 [l, mid - 1] 中寻找。
java 实现
public int search(int[] nums, int target) {
int n = nums.length;
if (n == 0) {
return -1;
}
if (n == 1) {
return nums[0] == target ? 0 : -1;
}
int l = 0, r = n - 1;
while (l <= r) {
int mid = (l + r) / 2;
if (nums[mid] == target) {
return mid;
}
if (nums[0] <= nums[mid]) {
if (nums[0] <= target && target < nums[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
} else {
if (nums[mid] < target && target <= nums[n - 1]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return -1;
}
复杂度
时间复杂度: O(logn),其中 n 为 nums 数组的大小。整个算法时间复杂度即为二分查找的时间复杂度 O(logn)。
空间复杂度: O(1)。我们只需要常数级别的空间存放变量。
81. 搜索旋转排序数组 II Search in Rotated Sorted Array II
题目
已知存在一个按非降序排列的整数数组 nums ,数组中的值不必互不相同。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转 ,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。
例如, [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。
给你 旋转后 的数组 nums 和一个整数 target ,请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ,则返回 true ,否则返回 false 。
你必须尽可能减少整个操作步骤。
例子
示例 1:
输入:nums = [2,5,6,0,0,1,2], target = 0
输出:true
示例 2:
输入:nums = [2,5,6,0,0,1,2], target = 3
输出:false
```
进阶:
这是 搜索旋转排序数组 的延伸题目,本题中的 nums 可能包含重复元素。
这会影响到程序的时间复杂度吗?会有怎样的影响,为什么?
## 思路
整体和 T33 类似,但是因为包含重复元素,所以略微复杂些。
对于数组中有重复元素的情况,二分查找时可能会有 `a[l]=a[mid]=a[r]`,此时无法判断区间 [l,mid] 和区间 [mid+1,r] 哪个是有序的。
例如 nums=[3,1,2,3,3,3,3],target=2,首次二分时无法判断区间 [0,3] 和区间 [4,6] 哪个是有序的。
对于这种情况,我们只能将当前二分区间的左边界加一,右边界减一,然后在新区间上继续二分查找。
## java 实现
```java
public boolean search(int[] nums, int target) {
int n = nums.length;
if (n == 0) {
return false;
}
if (n == 1) {
return nums[0] == target;
}
int l = 0, r = n - 1;
while (l <= r) {
int mid = (l + r) / 2;
if (nums[mid] == target) {
return true;
}
// 处理一下
if (nums[l] == nums[mid] && nums[mid] == nums[r]) {
++l;
--r;
} else if (nums[l] <= nums[mid]) {
if (nums[l] <= target && target < nums[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
} else {
if (nums[mid] < target && target <= nums[n - 1]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return false;
}
复杂度
时间复杂度: O(logn),其中 n 为 nums 数组的大小。整个算法时间复杂度即为二分查找的时间复杂度 O(logn)。
空间复杂度: O(1)。我们只需要常数级别的空间存放变量。
153. 寻找旋转排序数组中的最小值
题目
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
例子
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
```
提示:
n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 中的所有整数 互不相同
nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
## 思路
还是那句话,有序的数组,查找元素使用二分法!
但是问题是,已经被旋转了,还能使用吗?
The minimum element must satisfy one of two conditions:
[4,5,6,7,0,1,2]
1) If rotate, A[min] < A[min - 1];
2) If not, A[0].
Therefore, we can use binary search: check the middle element, if it is less than previous one, then it is minimum.
If not, there are 2 conditions as well: If it is greater than both left and right element, then minimum element should be on its right, otherwise on its left.
## java 实现
```java
public int findMin(int[] nums) {
int start = 0;
int end = nums.length - 1;
while (start < end) {
int mid = (start +end) / 2;
// 如果是旋转的场景。不旋转的话,一定大于前面
// [4,5,6,7,0,1,2]
if(mid > 0 &&
nums[mid] < nums[mid-1]) {
return nums[mid];
}
// 如果当前元素比2边都大,那就是右边。
if(nums[mid] >= nums[start]
&& nums[mid] >= nums[end]) {
start = mid+1;
} else {
end = mid-1;
}
}
return nums[start];
}
154. 寻找旋转排序数组中的最小值 II
题目
和 153 类似,编程数组中的元素可能重复。
思路
首先,我们取 low = 0, high = nums.length-1
0 1 2 3 4
1)默认情况下,如果 nums[lo] < nums[hi] 那么我们返回 nums[lo] 因为数组从未旋转过,或者旋转过 n 次。
2)进入while循环后,我们检查
if nums[mid] > nums[hi] => lo = mid + 1 因为最小元素在数组的右半部分
2 3 4 0 1
else if nums[mid] < nums[hi] => hi = mid 因为最小元素在数组的左半部分
7 0 1 2 3 4 5 6
else => hi-- 处理重复值
然后我们返回 nums[hi]
java 实现
public int findMin(int[] nums) {
int low = 0, high = nums.length-1;
// default
if(nums[low] < nums[high]) {
return nums[low];
}
while (low < high) {
int mid = (low + high) / 2;
//1. 大于最大,在右边
if(nums[mid] > nums[high]) {
low = mid+1;
} else if(nums[mid] < nums[high]) {
//2. 小于最大,则在左边
high = mid;
} else {
// 重复
high--;
}
}
return nums[high];
}
小结
可以看到有序的数组,再处理一个元素的时候,我们首先应该使用二分法。
只不过会有一些限制,但是核心思路不会变化。
开源地址
为了便于大家学习,所有实现均已开源。欢迎 fork + star~
参考资料
https://leetcode.cn/problems/search-in-rotated-sorted-array/
https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array/
