缘起
一个不会解的问题
https://leetcode.com/problems/combination-sum/
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:
输入:candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
提示:
1 <= candidates.length <= 30 1 <= candidates[i] <= 200 candidate 中的每个元素都是独一无二的。 1 <= target <= 500
最简单的思路
首先对列表进行排序。
然后遍历获取对应的子元素。
但是就存在两个问题:
(1)如何知道一个数,是由那些元素的和组成的呢?
(2)如何可以重复添加呢?
发现如果只是简单的穷举,这一题基本是废了。
分析思路
根据示例 1:输入: candidates = [2, 3, 6, 7],target = 7。
-
候选数组里有 2,如果找到了组合总和为 7 - 2 = 5 的所有组合,再在之前加上 2 ,就是 7 的所有组合;
-
同理考虑 3,如果找到了组合总和为 7 - 3 = 4 的所有组合,再在之前加上 3 ,就是 7 的所有组合,依次这样找下去。
ps:这样思考的好处就是将问题简单化,一个数 = 数1 + 数2(组合)。其中数1在列表中,我们只需要找到所有 数2 的组合即可。有一点递归的味道。
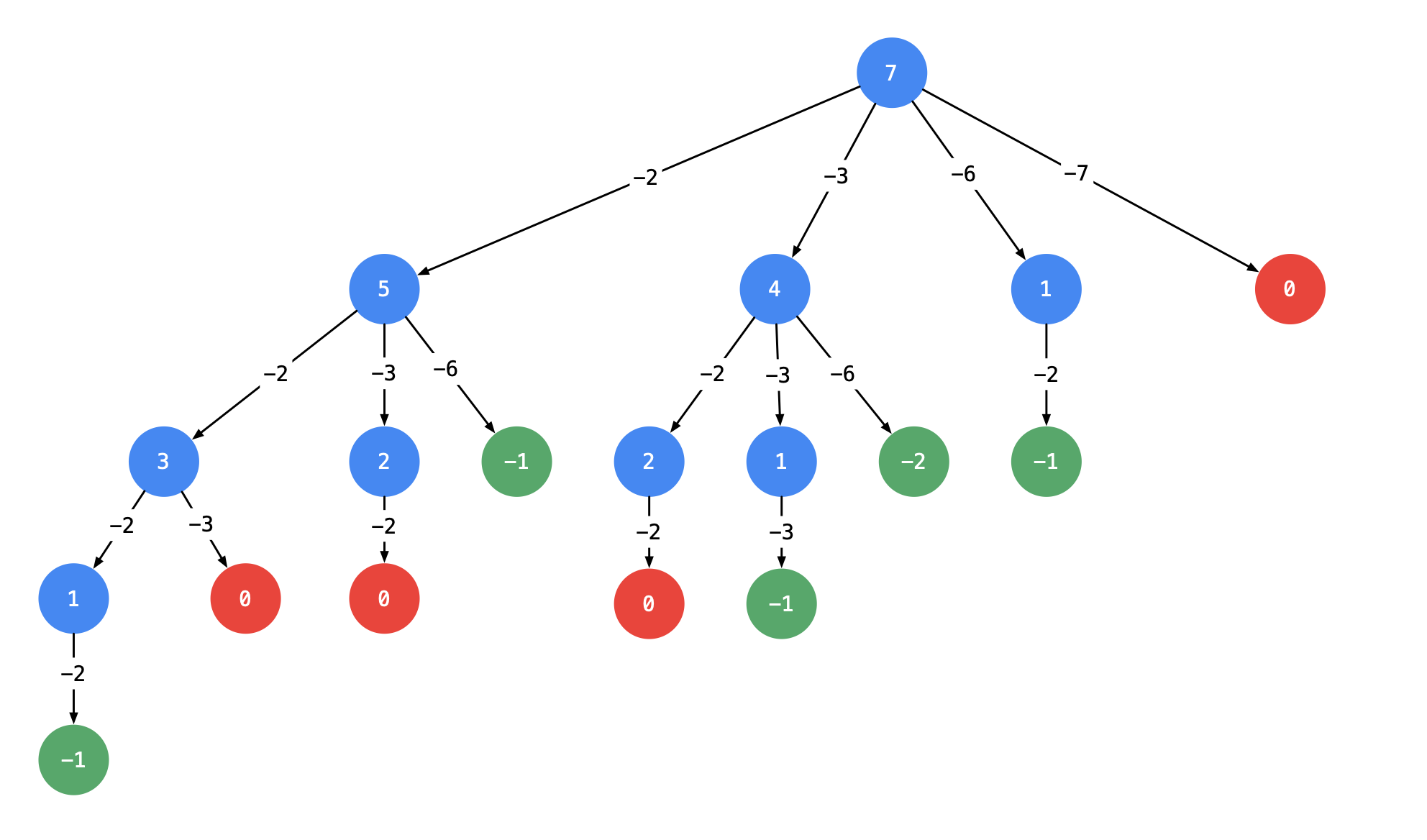
树型图
以输入:candidates = [2, 3, 6, 7], target = 7 为例:
说明:
以 target = 7 为 根结点 ,创建一个分支的时 做减法 ;
每一个箭头表示:从父亲结点的数值减去边上的数值,得到孩子结点的数值。边的值就是题目中给出的 candidate 数组的每个元素的值;
减到 0 或者负数的时候停止,即:结点 0 和负数结点成为叶子结点;
所有从根结点到结点 0 的路径(只能从上往下,没有回路)就是题目要找的一个结果。
这棵树有 4 个叶子结点的值 0,对应的路径列表是 [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]],而示例中给出的输出只有 [[7], [2, 2, 3]]。
即:题目中要求每一个符合要求的解是 不计算顺序 的。
下面我们分析为什么会产生重复。
数据为什么重复
产生重复的原因是:在每一个结点,做减法,展开分支的时候,由于题目中说 每一个元素可以重复使用,我们考虑了 所有的 候选数,因此出现了重复的列表。
hash 去重
一种简单的去重方案是借助哈希表的天然去重的功能,但实际操作一下,就会发现并没有那么容易。
ps: 也不是不能做,但是感觉性能会比较差。
个人思路:
(1)获取到所有的结果列表,尚未去重
(2)去每一个列表进行排序
(3)重新添加到列表中时,移除完全一致的列表。
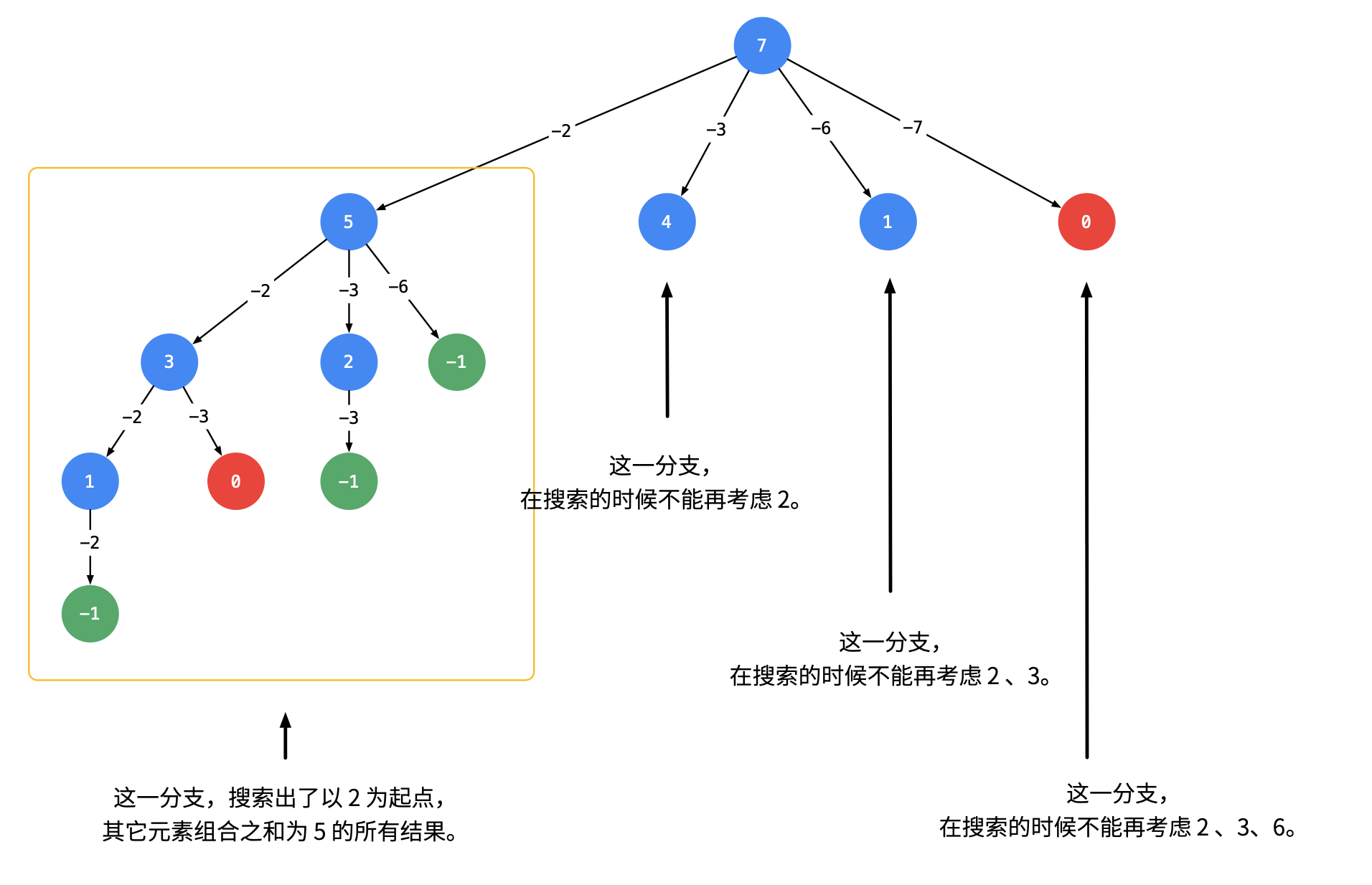
搜索去重
可不可以在搜索的时候就去重呢?
答案是可以的。
遇到这一类相同元素不计算顺序的问题,我们在搜索的时候就需要 按某种顺序搜索。
具体的做法是:每一次搜索的时候设置 下一轮搜索的起点 begin,请看下图。
即:从每一层的第 2 个结点开始,都不能再搜索产生同一层结点已经使用过的 candidate 里的元素。
ps: 因为每一个分支,都是把所有的可能罗列出来(不遗漏),我们后面的禁止使用已经使用的,就可以保证不重复了。
剪枝提速
根据上面画树形图的经验,如果 target 减去一个数得到负数,那么减去一个更大的树依然是负数,同样搜索不到结果。
基于这个想法,我们可以对输入数组进行排序,添加相关逻辑达到进一步剪枝的目的;
排序是为了提高搜索速度,对于解决这个问题来说非必要。但是搜索问题一般复杂度较高,能剪枝就尽量剪枝。
实际工作中如果遇到两种方案拿捏不准的情况,都试一下。
只有这一种方式吗?
感觉不需要排序+剪枝吧,把递归结束条件写在方法最前面 if(target < 0 || candidates == null || candidates.length == 0){ return; } 不是一样?
假如数组的长度很长,排序反而耗时。
代码实现
最经典的实现如下:
/**
* 思路:
*
* (1)回溯
* (2)剪枝算法优化
*
* @author https://github.com/houbb/
* @param candidates 候选集
* @param target 目标值
* @return 结果
*/
public List<List<Integer>> combinationSum(int[] candidates, int target) {
//1. 排序,是为了剪枝算法。实际不是必要的
Arrays.sort(candidates);
List<List<Integer>> results = new ArrayList<>();
// 核心算法
backtrack(results, new ArrayList<>(), candidates, target, 0);
return results;
}
/**
* 回溯算法
* @param results 结果
* @param tempList 临时列表
* @param candidates 候选数组
* @param remain 剩余值
* @param begin 开始索引
* @since v38
*/
private void backtrack(List<List<Integer>> results, List<Integer> tempList,
int[] candidates, int remain, int begin) {
//1. 如果小于0,直接剪枝
if(remain < 0) {
return;
} else if(remain == 0) {
// 需要的结果(使用一个新的列表,而不是直接存放原始列表,否则数据会被更新)
results.add(new ArrayList<>(tempList));
} else {
// 在所有的剩余集合中,选择信息
for(int i = begin; i < candidates.length; i++) {
// 放入目标元素
tempList.add(candidates[i]);
// 继续拆分剩余的集合组合
// 从 第 i 个元素开始,因为允许重复使用
backtrack(results, tempList, candidates, remain - candidates[i], i);
// 回溯
tempList.remove(tempList.size()-1);
}
}
}
经过实际测试,Arrays.sort(candidates); 在这里并不是必需的。
还能优化吗?
当然,还是有优化的空间的。
那就是上面的算法,实际上有两步:
-
执行 remain-candidates[i]
-
判断 remain < 0
实际上可以优化一下,减少一次运算:
实现如下:
/**
* 思路:
*
* (1)回溯
* (2)剪枝算法优化
*
* @author https://github.com/houbb/
* @param candidates 候选集
* @param target 目标值
* @return 结果
*/
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> results = new ArrayList<>();
backtrack(candidates, target, new ArrayList<>(), 0, results);
return results;
}
private void backtrack(int[] candidates, int remain, List<Integer> tempList,
int begin, List<List<Integer>> results) {
if (remain == 0) {
results.add(new ArrayList<>(tempList));
return;
}
for (int i = begin; i < candidates.length; i++) {
// 这里实际上优化了 2 步:
// 1. candidates 排序并不是必须的
// 2. 单次回溯,根据大小判断,避免一次减法+大小比较
int current = candidates[i];
if (remain >= current) {
tempList.add(current);
// 元素可以重复使用,所以取 i
backtrack(candidates, remain - current, tempList, i, results);
tempList.remove(tempList.size() - 1);
}
}
}
题目的变形
如果不允许重复取出元素呢?
实际上,这里我们就需要排序了。
经典实现如下:
/**
* 思路:
*
* (1)回溯
* (2)剪枝算法优化
*
* @author https://github.com/houbb/
* @param candidates 候选集
* @param target 目标值
* @return 结果
*/
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
// 这个排序时必须的,用于去重
Arrays.sort(candidates);
List<List<Integer>> results = new ArrayList<>();
// 核心算法
backtrack(results, new ArrayList<>(), candidates, target, 0);
return results;
}
/**
* 回溯算法
* @param results 结果
* @param tempList 临时列表
* @param candidates 候选数组
* @param remain 剩余值
* @param begin 开始索引
* @since v40
*/
private void backtrack(List<List<Integer>> results, List<Integer> tempList,
int[] candidates, int remain, int begin) {
if(remain < 0) {
return;
} else if(remain == 0) {
results.add(new ArrayList<>(tempList));
} else {
// 核心处理
for(int i = begin; i < candidates.length; i++) {
// 如何跳过重复的信息
if(i > begin && candidates[i] == candidates[i-1]) {
continue;
}
int current = candidates[i];
tempList.add(current);
backtrack(results, tempList, candidates, remain-current, i+1);
tempList.remove(tempList.size()-1);
}
}
}
参考资料
https://leetcode.com/problems/combination-sum/discuss/16502/A-general-approach-to-backtracking-questions-in-Java-(Subsets-Permutations-Combination-Sum-Palindrome-Partitioning)
https://leetcode-cn.com/problems/combination-sum/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-m-2/