题目 127
A transformation sequence from word beginWord to word endWord using a dictionary wordList is a sequence of words beginWord -> s1 -> s2 -> … -> sk such that:
Every adjacent pair of words differs by a single letter.
Every si for 1 <= i <= k is in wordList. Note that beginWord does not need to be in wordList.
sk == endWord
Given two words, beginWord and endWord, and a dictionary wordList, return the number of words in the shortest transformation sequence from beginWord to endWord, or 0 if no such sequence exists.
Example 1:
Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
Output: 5
Explanation: One shortest transformation sequence is "hit" -> "hot" -> "dot" -> "dog" -> cog", which is 5 words long.
Example 2:
Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
Output: 0
Explanation: The endWord "cog" is not in wordList, therefore there is no valid transformation sequence.
Constraints:
1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord, endWord, and wordList[i] consist of lowercase English letters.
beginWord != endWord
All the words in wordList are unique.
PS:吐槽一下 127 这个题目,应该是 126 的基础,而不是反过来。
思路详解
我发现自己对这个问题的理解还是不够深入。
所以先学习一下别人的思路。
所以,所有这些问题都要求我们做,就是只使用列表中的单词找到从起始单词到结束单词的最短路径。
现在任何时候你想到,找到你应该立即想到的最短序列,好吧,我需要使用一些最短路径算法,比如广度优先搜索 BFS。
让我们举个例子:-
start = be
end = ko
words = ["ce", "mo", "ko", "me", "co"]
所以,使用这个单词列表,我们有 4 条不同的路径可以从我们的开始到结束单词。
所以,我们可以从“be”——“ce”——“co”——“ko”
从起始词到结束词还有其他路径,但是我们只考虑最短路径,即序列中单词数量最少的路径,在这种情况下,它将是:

因此,在典型的广度优先搜索中,我们使用队列,它将存储序列中的每个字符串,然后我们还将拥有称为 changes 的整数值,它最终将从我们的函数返回,它将跟踪如何 我们在序列中有很多变化。
ps: 这里还是保留原文,同时使用谷歌翻译比较好,避免混乱。
So, we intialize our queue that have starting word inside of it i.e. "be", then our changes variable is going to start at 1, this is because at minimum we going to have starting word in our minimum. And finally we have a set which will keep track's of node that have been visited, in this case we just keeping track of string that we have already added inside our queue.
所以,我们初始化我们的队列 queue,里面有起始词,即“be”,然后我们的 changes 变量将从 1 开始,这是因为至少我们将在我们的最小值中有起始词。
最后我们有一个集合,它将跟踪已访问的节点,在这种情况下,我们只跟踪我们已经添加到队列中的字符串。
queue = ["be" ] //存放每一个字符串
changes = 1 // 最后的结果
set = ["be" ] // 已经访问的节点
So, to start of our bfs, we take "be" off from our queue & we can only change one character at a time.
So, first we gonna check by changing the character b, if we can form another word inside our word list.
So, we try ae, which is not in our word list. Then, be is already in our set, so we can't use that. Now we try ce and we have that word inside our word list. With that means add ce in our queue.
Then we check de, fe and so on............ until we get to me which is inside our word list, so we add me inside our word list as well.
So, all that way we check all the way down to ze and there is no other words that we add by changing b to another character.
因此,为了开始我们的 bfs,我们从队列中删除“be”并且我们一次只能更改一个字符。
所以,首先我们要通过改变字符 b 来检查我们是否可以在我们的单词列表中形成另一个单词。
所以,我们尝试 ae,它不在我们的单词列表中。 然后,be 已经在我们的集合中,所以我们不能使用它。 现在我们尝试 ce 并且我们的单词列表中有那个单词。 这意味着在我们的队列中添加 ce。
然后我们检查 de、fe 等等......直到我们找到 me ,它在我们的单词列表中,所以我们也将 me 添加到我们的单词列表中。
因此,我们一直检查到 ze ,并且没有通过将 b 更改为另一个字符来添加其他单词。
ps: 这里的比较其实有一个技巧。那就是,因为 wordList 中数量可能会比较多,所以 wordlist 中循环对比,反而是比较麻烦的办法。直接 a-z 对每一位进行变化,然后判断结果是否存在,这种性能可能比较好的。

So, now we need to check first index. So, by changing the character e from be to something else if we form an another word.
So, we gonna check ba, bb all the way down to bz. However none of the word inside our word list.
Adittionaly, thw word ce & me are going to get added inside our set. To show, that we have already visited those words.
所以,现在我们需要检查第一个索引。
因此,如果我们形成另一个词,则通过将字符 e 从 be 更改为其他字符。
所以,我们要检查 ba、bb 一直到 bz。 但是我们的单词列表中没有单词。
此外,单词 ce 和 me 将添加到我们的集合中。 表明,我们已经访问过这些词。

PS: 就是遍历每一个字符,然后对每一位 a-z 变换。
And then we gonna perform same logic as before. We poll from our queue we take ce off from our queue. And we check if by changing any character we can form another word.
So, we gonna see if we change first character c to another character to form a word. So, we gonna try ae , be, ce which is already in our set doesn't count de, ee all the ay down to ze and none of the word included inside our word list.
然后我们将执行与之前相同的逻辑。
我们从我们的队列中轮询我们从我们的队列中删除。
我们检查是否可以通过更改任何字符来组成另一个词。
因此,我们将看看是否将第一个字符 c 更改为另一个字符以组成一个单词。
所以,我们要尝试 ae , be , ce 已经在我们的集合中的不包括 de , ee 所有的 ay 到 ze 并且没有一个词包含在我们的单词列表中。

Now we gonna see if we change e from ce to another character.
So, we gonna try ca, cb and so on..... eventually we get to the word co which is in our word list. So what that means we gonna add co to our queue & our set.
现在我们来看看是否将 e 从 ce 更改为另一个字符。
所以,我们将尝试 ca、cb 等等……最终我们得到了单词列表中的单词 co。 那么这意味着我们要将 co 添加到我们的队列和集合中。

java 实现
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
//fast-return
Set<String> wordSet = new HashSet<>(wordList);
if(!wordSet.contains(endWord)) {
return 0;
}
// 存放 BFS 元素,初始为开始词
Queue<String> queue = new LinkedList<>();
queue.add(beginWord);
// 已经访问过得元素
Set<String> visited = new HashSet<>();
visited.add(beginWord);
// 变化的结果
int result = 1;
System.out.println("queue: " + queue + "; visited: " + visited + "; result: " + result);
// 遍历整个队列
while(!queue.isEmpty()){
int size = queue.size();
for(int i = 0; i < size; i++){
// 获取队列中的第一个元素
String word = queue.poll();
// 如果和终止词相同,则迭代结束,直接返回结果。
if(word.equals(endWord)) {
return result;
}
for(int j = 0; j < word.length(); j++){
for(int k = 'a'; k <= 'z'; k++){
// 穷举 a-z 变化 word 单词的每一位,
char[] arr = word.toCharArray();
arr[j] = (char) k;
String str = new String(arr);
// 如果单词中有这个词
// 而且已经没有处理过,则加入进来。
if(wordSet.contains(str)
&& !visited.contains(str)){
// 更新 queue 中元素
queue.add(str);
// 更新访问过的元素
visited.add(str);
System.out.println("queue: " + queue + "; visited: " + visited + "; result: " + result);
}
}
}
}
++result;
}
// 无匹配
return 0;
}
输出一下日志:
queue: [be]; visited: [be]; result: 1
queue: [ce]; visited: [ce, be]; result: 1
queue: [ce, me]; visited: [ce, be, me]; result: 1
queue: [me, co]; visited: [ce, be, me, co]; result: 2
queue: [co, mo]; visited: [ce, mo, be, me, co]; result: 2
queue: [mo, ko]; visited: [ce, mo, be, ko, me, co]; result: 3
V2 性能优化
但是发现,这个算法的性能比较差。
排名第一的算法:
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
Set<String> beginSet = new HashSet<>();
Set<String> endSet = new HashSet<>();
beginSet.add(beginWord);
endSet.add(endWord);
Set<String> wordSet = new HashSet<>(wordList);
if(!wordSet.contains(endWord)) {
return 0;
}
return search(beginSet, endSet, wordSet, 1);
}
private int search(Set<String> beginSet, Set<String> endSet, Set<String> wordSet, int result){
if(beginSet.isEmpty() || endSet.isEmpty()) {
return 0;
}
result++;
// 从字典中,移除了开始的集合?
wordSet.removeAll(beginSet);
Set<String> nextSet = new HashSet<>();
// 遍历开始的 set
for(String str : beginSet){
// 这里核心算法应该是类似的。
char[] chs = str.toCharArray();
for(int i = 0; i < chs.length; i++){
char c = chs[i];
for(char j = 'a'; j <= 'z'; j++){
chs[i] = j;
// a-z 的变化开始词的每一个字符,如果字典中不存在,则跳过。
// 如果和终止词相同,则结束。
String tmp = new String(chs);
if(!wordSet.contains(tmp)) {
continue;
}
if(endSet.contains(tmp)) {
return result;
}
nextSet.add(tmp);
}
chs[i] = c;
}
}
// 这里是优化的原因吗?
// 其实最初的 endSet 中只有一个元素,那就是 endword 终止词
// 这里会进行对比,入参时交换了 endSet 和 nextSet 的顺序??
// serch 中,最大的计算量在于对 benginSet 的 a-z 穷举变化,所以数量越小越好。
return nextSet.size() > endSet.size() ? search(endSet, nextSet, wordSet, result) : search(nextSet, endSet, wordSet, result);
}
PS: 这个为什么会快了这么多呢?
题目 126
Word Ladder II
A transformation sequence from word beginWord to word endWord using a dictionary wordList is a sequence of words beginWord -> s1 -> s2 -> … -> sk such that:
Every adjacent pair of words differs by a single letter.
Every si for 1 <= i <= k is in wordList. Note that beginWord does not need to be in wordList.
sk == endWord
Given two words, beginWord and endWord, and a dictionary wordList, return all the shortest transformation sequences from beginWord to endWord, or an empty list if no such sequence exists.
Each sequence should be returned as a list of the words [beginWord, s1, s2, …, sk].
Ex
Example 1:
Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
Output: [["hit","hot","dot","dog","cog"],["hit","hot","lot","log","cog"]]
Explanation: There are 2 shortest transformation sequences:
"hit" -> "hot" -> "dot" -> "dog" -> "cog"
"hit" -> "hot" -> "lot" -> "log" -> "cog"
Example 2:
Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
Output: []
Explanation: The endWord "cog" is not in wordList, therefore there is no valid transformation sequence.
Constraints:
-
1 <= beginWord.length <= 5
-
endWord.length == beginWord.length
-
1 <= wordList.length <= 500
-
wordList[i].length == beginWord.length
-
beginWord, endWord, and wordList[i] consist of lowercase English letters.
-
beginWord != endWord
-
All the words in wordList are unique.
-
The sum of all shortest transformation sequences does not exceed 10^5.
第一感觉
这一题需要使用 backtracking 才能解决。
其实 wordlist 中不包含 endword,而是通过一个变化,可以到 endword,这题也是一样的。
这一题,换而言之,实际上在计算两个 word 之间的编辑距离为1,比编辑距离简单一点,因为只有替换,没有增删换顺序。
【思路】
(1)判断 wordlist 是否包含 endword,fast-return
(2)从 endword 开始推理,依次获得每一个 word 获取所有编辑距离为1的单词。
所以这里可以使用 HashMap: key: word, hashMap 就是对这个 word 每一个 char 的 26 中变化。
Set: 为了提升判断 char 变化之后,wordlist 中是否存在,可以把 wordlist 首先转换为 set。查找复杂度变为 O(1)。
然后构建有效的 change1HashMap。
(3)如何回溯呢?
3.1 change1HashMap.get(endWord) 可以得到所有差距为1的映射 list,不存在则终止
3.2 遍历 3.2 中的 list,不断重复这个过程,这里就需要用到回溯。
3.3 直到最后没有映射 list,或者结果就是 starword。终止。
暂时不考虑剪枝。
算法实现
V1 版本
最简单的,不考虑性能的实现。
/**
* 最小路径大小
*/
private int minPathSize = Integer.MAX_VALUE;
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
List<List<String>> resultList = new ArrayList<>();
List<String> tempList = new ArrayList<>();
tempList.add(beginWord);
// 对数据提前处理?
Map<String, List<String>> changeWordMap = buildWordChangeMap(beginWord, wordList);
this.backtrack(resultList, beginWord, endWord, changeWordMap, tempList, 0);
// 最短路径,而不是所有路径?
return filterList(resultList);
}
public List<List<String>> filterList(List<List<String>> allList) {
if(allList.size() <= 0) {
return allList;
}
// 过滤
List<List<String>> resultList = new ArrayList<>();
for(List<String> paths : allList) {
if(paths.size() <= minPathSize) {
resultList.add(paths);
}
}
return resultList;
}
/**
* 终止条件
*
* @param resultList 结果
* @param beginWord 开始词
* @param endWord 终止词
* @param changeWordMap 变更为1的字典映射
* @param tempList 存放临时的路径
*/
private void backtrack(List<List<String>> resultList,
String beginWord,
String endWord,
Map<String, List<String>> changeWordMap,
List<String> tempList,
int index) {
List<String> beginWordChangeOneList = changeWordMap.get(beginWord);
if(beginWordChangeOneList == null
|| tempList.size() > minPathSize) {
// 什么时候中断呢?
return;
} else if(beginWord.equals(endWord)) {
// 更新大小
if(tempList.size() < minPathSize) {
minPathSize = tempList.size();
}
// 过滤掉不是最小的
resultList.add(new ArrayList<>(tempList));
// 但是这样,还是可能会导致添加的元素长度过长
// 比如第一次长度为10, 后续越来越少,只有最小的其实才符合。
} else {
// 更新开始信息
// 在所有的剩余集合中,选择信息
for(int i = 0; i < beginWordChangeOneList.size(); i++) {
String newBeginWord = beginWordChangeOneList.get(i);
// 这里有一个问题,其实单词不应该被重复使用,否则会死循环。
if(tempList.contains(newBeginWord)) {
continue;
}
tempList.add(newBeginWord);
// 什么时候回溯?
backtrack(resultList, newBeginWord, endWord, changeWordMap, tempList, index+1);
// backtrack
tempList.remove(tempList.size()-1);
}
}
}
/**
* 构建1个变换量的词库映射
*
* wordlist 不超过 500 个。
* 如何找到变化为1的单词呢?
*
* 其实也就是2个单词不同的字母只有1个。
*
*
*
* 【发现测试用例7,并不需要保证次序】
* PS: 这里这种处理存在一个问题,那就是必须在后边的才行。
* 从而保证一个顺序:beginWord -> s1 -> s2 -> ... -> sk
*
* @param beginWord 开始词
* @param wordList 单词列表
* @return 结果
*/
private Map<String, List<String>> buildWordChangeMap(String beginWord, List<String> wordList) {
Map<String, List<String>> resultMap = new HashMap<>();
// 开始词
resultMap.put(beginWord, getMappingList(beginWord, wordList));
// 2 次迭代
for(int i = 0; i < wordList.size(); i++) {
String s = wordList.get(i);
List<String> tempList = getMappingList(s, wordList);
resultMap.put(s, tempList);
}
return resultMap;
}
private List<String> getMappingList(String word, List<String> wordList) {
List<String> tempList = new ArrayList<>();
for(int i = 0; i < wordList.size(); i++) {
String t = wordList.get(i);
// 差距为1的单词
if(isDifferOne(word, t)) {
tempList.add(t);
}
}
return tempList;
}
/**
* 两个字符的差距是否为 1
* @param s 原始
* @param t 目标
* @return 结果
*/
private boolean isDifferOne(String s, String t) {
int differCount = 0;
for(int i = 0; i < s.length(); i++) {
char sc = s.charAt(i);
char tc = t.charAt(i);
if(sc != tc) {
differCount++;
}
}
return differCount == 1;
}
V2 如何优化性能?
这个实现本身应该是没问题的,不过会超时。
beginWord ="qa"
endWord = "sq"
wordList =
["si","go","se","cm","so","ph","mt","db","mb","sb","kr","ln","tm","le","av","sm","ar","ci","ca","br","ti","ba","to","ra","fa","yo","ow","sn","ya","cr","po","fe","ho","ma","re","or","rn","au","ur","rh","sr","tc","lt","lo","as","fr","nb","yb","if","pb","ge","th","pm","rb","sh","co","ga","li","ha","hz","no","bi","di","hi","qa","pi","os","uh","wm","an","me","mo","na","la","st","er","sc","ne","mn","mi","am","ex","pt","io","be","fm","ta","tb","ni","mr","pa","he","lr","sq","ye"]
这个 CASE,直接 GG。
那么问题到底出在哪里呢?
其实,如果如果可以首先获取到最短的路径,然后剪枝,应该会快很多。
也可以节省最后的处理。
不过通过 debug 发现,最耗时的还是中间回溯这部分。
我们结合 T127 的最短路径,然后测试进行长度的剪枝。
import java.util.*;
public class T126_WordLadderIIV3 {
/**
* 最小路径大小
*/
private int minPathSize = 0;
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
// dfs 首先获取最小路径
minPathSize = ladderLength(beginWord, endWord, wordList);
List<List<String>> resultList = new ArrayList<>();
// 快速失败
if(minPathSize <= 0) {
return resultList;
}
List<String> tempList = new ArrayList<>();
tempList.add(beginWord);
// 对数据提前处理?
//map 构建几毫秒,耗时不多。不过应该可以优化。
Map<String, List<String>> changeWordMap = buildWordChangeMap(beginWord, wordList);
this.backtrack(resultList, beginWord, endWord, changeWordMap, tempList, 0);
// 最短路径,而不是所有路径?
return resultList;
}
/**
* 127 中的,获取最小路径
* @param beginWord 开始
* @param endWord 结束
* @param wordList 单词字典
* @return 结果
*/
private int ladderLength(String beginWord, String endWord, List<String> wordList) {
Set<String> beginSet = new HashSet<>();
Set<String> endSet = new HashSet<>();
beginSet.add(beginWord);
endSet.add(endWord);
Set<String> wordSet = new HashSet<>(wordList);
if(!wordSet.contains(endWord)) {
return 0;
}
return bfs(beginSet, endSet, wordSet, 1);
}
private int bfs(Set<String> beginSet, Set<String> endSet, Set<String> wordSet, int result){
if(beginSet.isEmpty() || endSet.isEmpty()) {
return 0;
}
result++;
// 从字典中,移除了开始的集合?
wordSet.removeAll(beginSet);
Set<String> nextSet = new HashSet<>();
// 遍历开始的 set
for(String str : beginSet){
// 这里核心算法应该是类似的。
char[] chs = str.toCharArray();
for(int i = 0; i < chs.length; i++){
char c = chs[i];
for(char j = 'a'; j <= 'z'; j++){
chs[i] = j;
// a-z 的变化开始词的每一个字符,如果字典中不存在,则跳过。
// 如果和终止词相同,则结束。
String tmp = new String(chs);
if(!wordSet.contains(tmp)) {
continue;
}
if(endSet.contains(tmp)) {
return result;
}
nextSet.add(tmp);
}
chs[i] = c;
}
}
// 这里是优化的原因吗?
// 其实最初的 endSet 中只有一个元素,那就是 endword 终止词
// 这里会进行对比,入参时交换了 endSet 和 nextSet 的顺序??
// serch 中,最大的计算量在于对 benginSet 的 a-z 穷举变化,所以数量越小越好。
return nextSet.size() > endSet.size() ? bfs(endSet, nextSet, wordSet, result) : bfs(nextSet, endSet, wordSet, result);
}
/**
* 终止条件
*
* @param resultList 结果
* @param beginWord 开始词
* @param endWord 终止词
* @param changeWordMap 变更为1的字典映射
* @param tempList 存放临时的路径
*/
private void backtrack(List<List<String>> resultList,
String beginWord,
String endWord,
Map<String, List<String>> changeWordMap,
List<String> tempList,
int index) {
List<String> beginWordChangeOneList = changeWordMap.get(beginWord);
if(beginWordChangeOneList == null
|| tempList.size() > minPathSize) {
// 什么时候中断呢?
return;
} else if(beginWord.equals(endWord)) {
// 过滤掉不是最小的
// 什么时候符合结果?
resultList.add(new ArrayList<>(tempList));
// 但是这样,还是可能会导致添加的元素长度过长
// 比如第一次长度为10, 后续越来越少,只有最小的其实才符合。
} else {
// 更新开始信息
// 在所有的剩余集合中,选择信息
for(int i = 0; i < beginWordChangeOneList.size(); i++) {
String newBeginWord = beginWordChangeOneList.get(i);
// 这里有一个问题,其实单词不应该被重复使用,否则会死循环。
if(tempList.contains(newBeginWord)) {
continue;
}
tempList.add(newBeginWord);
// 什么时候回溯?
backtrack(resultList, newBeginWord, endWord, changeWordMap, tempList, index+1);
// backtrack
tempList.remove(tempList.size()-1);
}
}
}
/**
* 构建1个变换量的词库映射
*
* wordlist 不超过 500 个。
* 如何找到变化为1的单词呢?
*
* 其实也就是2个单词不同的字母只有1个。
*
*
*
* 【发现测试用例7,并不需要保证次序】
* PS: 这里这种处理存在一个问题,那就是必须在后边的才行。
* 从而保证一个顺序:beginWord -> s1 -> s2 -> ... -> sk
*
* @param beginWord 开始词
* @param wordList 单词列表
* @return 结果
*/
private Map<String, List<String>> buildWordChangeMap(String beginWord, List<String> wordList) {
Map<String, List<String>> resultMap = new HashMap<>();
// 开始词
resultMap.put(beginWord, getMappingList(beginWord, wordList));
// 2 次迭代
for(int i = 0; i < wordList.size(); i++) {
String s = wordList.get(i);
List<String> tempList = getMappingList(s, wordList);
resultMap.put(s, tempList);
}
return resultMap;
}
private List<String> getMappingList(String word, List<String> wordList) {
List<String> tempList = new ArrayList<>();
for(int i = 0; i < wordList.size(); i++) {
String t = wordList.get(i);
// 差距为1的单词
if(isDifferOne(word, t)) {
tempList.add(t);
}
}
return tempList;
}
/**
* 两个字符的差距是否为 1
* @param s 原始
* @param t 目标
* @return 结果
*/
private boolean isDifferOne(String s, String t) {
int differCount = 0;
for(int i = 0; i < s.length(); i++) {
char sc = s.charAt(i);
char tc = t.charAt(i);
if(sc != tc) {
differCount++;
}
}
return differCount == 1;
}
}
结果又超时在了下面的 CASE:
beginWord =
"cet"
endWord =
"ism"
wordList =
["kid","tag","pup","ail","tun","woo","erg","luz","brr","gay","sip","kay","per","val","mes","ohs","now","boa","cet","pal","bar","die","war","hay","eco","pub","lob","rue","fry","lit","rex","jan","cot","bid","ali","pay","col","gum","ger","row","won","dan","rum","fad","tut","sag","yip","sui","ark","has","zip","fez","own","ump","dis","ads","max","jaw","out","btu","ana","gap","cry","led","abe","box","ore","pig","fie","toy","fat","cal","lie","noh","sew","ono","tam","flu","mgm","ply","awe","pry","tit","tie","yet","too","tax","jim","san","pan","map","ski","ova","wed","non","wac","nut","why","bye","lye","oct","old","fin","feb","chi","sap","owl","log","tod","dot","bow","fob","for","joe","ivy","fan","age","fax","hip","jib","mel","hus","sob","ifs","tab","ara","dab","jag","jar","arm","lot","tom","sax","tex","yum","pei","wen","wry","ire","irk","far","mew","wit","doe","gas","rte","ian","pot","ask","wag","hag","amy","nag","ron","soy","gin","don","tug","fay","vic","boo","nam","ave","buy","sop","but","orb","fen","paw","his","sub","bob","yea","oft","inn","rod","yam","pew","web","hod","hun","gyp","wei","wis","rob","gad","pie","mon","dog","bib","rub","ere","dig","era","cat","fox","bee","mod","day","apr","vie","nev","jam","pam","new","aye","ani","and","ibm","yap","can","pyx","tar","kin","fog","hum","pip","cup","dye","lyx","jog","nun","par","wan","fey","bus","oak","bad","ats","set","qom","vat","eat","pus","rev","axe","ion","six","ila","lao","mom","mas","pro","few","opt","poe","art","ash","oar","cap","lop","may","shy","rid","bat","sum","rim","fee","bmw","sky","maj","hue","thy","ava","rap","den","fla","auk","cox","ibo","hey","saw","vim","sec","ltd","you","its","tat","dew","eva","tog","ram","let","see","zit","maw","nix","ate","gig","rep","owe","ind","hog","eve","sam","zoo","any","dow","cod","bed","vet","ham","sis","hex","via","fir","nod","mao","aug","mum","hoe","bah","hal","keg","hew","zed","tow","gog","ass","dem","who","bet","gos","son","ear","spy","kit","boy","due","sen","oaf","mix","hep","fur","ada","bin","nil","mia","ewe","hit","fix","sad","rib","eye","hop","haw","wax","mid","tad","ken","wad","rye","pap","bog","gut","ito","woe","our","ado","sin","mad","ray","hon","roy","dip","hen","iva","lug","asp","hui","yak","bay","poi","yep","bun","try","lad","elm","nat","wyo","gym","dug","toe","dee","wig","sly","rip","geo","cog","pas","zen","odd","nan","lay","pod","fit","hem","joy","bum","rio","yon","dec","leg","put","sue","dim","pet","yaw","nub","bit","bur","sid","sun","oil","red","doc","moe","caw","eel","dix","cub","end","gem","off","yew","hug","pop","tub","sgt","lid","pun","ton","sol","din","yup","jab","pea","bug","gag","mil","jig","hub","low","did","tin","get","gte","sox","lei","mig","fig","lon","use","ban","flo","nov","jut","bag","mir","sty","lap","two","ins","con","ant","net","tux","ode","stu","mug","cad","nap","gun","fop","tot","sow","sal","sic","ted","wot","del","imp","cob","way","ann","tan","mci","job","wet","ism","err","him","all","pad","hah","hie","aim"]
性能优化 V3
我们的 BFS 中,只用到了最小的长度。
但是没有构建对应的可到达边,这是比较浪费的。
整体感觉比较自然的算法如下:
he basic idea is:
1). Use BFS to find the shortest distance between start and end, tracing the distance of crossing nodes from start node to end node, and store node's next level neighbors to HashMap;
2). Use DFS to output paths with the same distance as the shortest distance from distance HashMap: compare if the distance of the next level node equals the distance of the current node + 1.
java 代码:
public class T126_WordLadderIIV_OTHER2 {
public List<List<String>> findLadders(String start, String end, List<String> wordList) {
HashSet<String> dict = new HashSet<>(wordList);
List<List<String>> res = new ArrayList<>();
// Neighbors for every node
HashMap<String, List<String>> nodeNeighbors = new HashMap<>();
// Distance of every node from the start node
HashMap<String, Integer> distance = new HashMap<>();
ArrayList<String> solution = new ArrayList<>();
dict.add(start);
bfs(start, end, dict, nodeNeighbors, distance);
dfs(start, end, nodeNeighbors, distance, solution, res);
return res;
}
/**
* BFS: Trace every node's distance from the start node (level by level).
* 1. 计算出最小路径长度
* 2. 记录临边和对应的长度
* @param start 开始词
* @param end 结束词
* @param dict 字典
* @param nodeNeighbors 临边
* @param distance 距离
*/
private void bfs(String start, String end, Set<String> dict,
HashMap<String, List<String>> nodeNeighbors,
HashMap<String, Integer> distance) {
for (String str : dict) {
nodeNeighbors.put(str, new ArrayList<>());
}
Queue<String> queue = new LinkedList<>();
queue.offer(start);
distance.put(start, 0);
while (!queue.isEmpty()) {
int count = queue.size();
boolean foundEnd = false;
for (int i = 0; i < count; i++) {
String cur = queue.poll();
int curDistance = distance.get(cur);
// 这里构建的可达边,比直接初始化构建要少很多。
ArrayList<String> neighbors = getNeighbors(cur, dict);
for (String neighbor : neighbors) {
nodeNeighbors.get(cur).add(neighbor);
// Check if visited
if (!distance.containsKey(neighbor)) {
distance.put(neighbor, curDistance + 1);
// Found the shortest path
if (end.equals(neighbor))
{
foundEnd = true;
} else {
queue.offer(neighbor);
}
}
}
}
if (foundEnd) {
break;
}
}
}
// Find all next level nodes.
private ArrayList<String> getNeighbors(String node, Set<String> dict) {
ArrayList<String> res = new ArrayList<>();
char[] chs = node.toCharArray();
for (char ch = 'a'; ch <= 'z'; ch++) {
for (int i = 0; i < chs.length; i++) {
if (chs[i] == ch) {
continue;
}
char oldCh = chs[i];
chs[i] = ch;
if (dict.contains(String.valueOf(chs))) {
res.add(String.valueOf(chs));
}
chs[i] = oldCh;
}
}
return res;
}
// DFS: output all paths with the shortest distance.
private void dfs(String cur, String end, HashMap<String, List<String>> nodeNeighbors,
HashMap<String, Integer> distance,
List<String> solution,
List<List<String>> res) {
solution.add(cur);
if (end.equals(cur)) {
res.add(new ArrayList<>(solution));
} else {
for (String next : nodeNeighbors.get(cur)) {
if (distance.get(next) == distance.get(cur) + 1) {
dfs(next, end, nodeNeighbors, distance, solution, res);
}
}
}
solution.remove(solution.size() - 1);
}
}
悲哀的是,这个算法在下面的 CASE 依然会超时:
beginWord =
"aaaaa"
endWord =
"ggggg"
wordList =
["aaaaa","caaaa","cbaaa","daaaa","dbaaa","eaaaa","ebaaa","faaaa","fbaaa","gaaaa","gbaaa","haaaa","hbaaa","iaaaa","ibaaa","jaaaa","jbaaa","kaaaa","kbaaa","laaaa","lbaaa","maaaa","mbaaa","naaaa","nbaaa","oaaaa","obaaa","paaaa","pbaaa","bbaaa","bbcaa","bbcba","bbdaa","bbdba","bbeaa","bbeba","bbfaa","bbfba","bbgaa","bbgba","bbhaa","bbhba","bbiaa","bbiba","bbjaa","bbjba","bbkaa","bbkba","bblaa","bblba","bbmaa","bbmba","bbnaa","bbnba","bboaa","bboba","bbpaa","bbpba","bbbba","abbba","acbba","dbbba","dcbba","ebbba","ecbba","fbbba","fcbba","gbbba","gcbba","hbbba","hcbba","ibbba","icbba","jbbba","jcbba","kbbba","kcbba","lbbba","lcbba","mbbba","mcbba","nbbba","ncbba","obbba","ocbba","pbbba","pcbba","ccbba","ccaba","ccaca","ccdba","ccdca","cceba","cceca","ccfba","ccfca","ccgba","ccgca","cchba","cchca","cciba","ccica","ccjba","ccjca","cckba","cckca","cclba","cclca","ccmba","ccmca","ccnba","ccnca","ccoba","ccoca","ccpba","ccpca","cccca","accca","adcca","bccca","bdcca","eccca","edcca","fccca","fdcca","gccca","gdcca","hccca","hdcca","iccca","idcca","jccca","jdcca","kccca","kdcca","lccca","ldcca","mccca","mdcca","nccca","ndcca","occca","odcca","pccca","pdcca","ddcca","ddaca","ddada","ddbca","ddbda","ddeca","ddeda","ddfca","ddfda","ddgca","ddgda","ddhca","ddhda","ddica","ddida","ddjca","ddjda","ddkca","ddkda","ddlca","ddlda","ddmca","ddmda","ddnca","ddnda","ddoca","ddoda","ddpca","ddpda","dddda","addda","aedda","bddda","bedda","cddda","cedda","fddda","fedda","gddda","gedda","hddda","hedda","iddda","iedda","jddda","jedda","kddda","kedda","lddda","ledda","mddda","medda","nddda","nedda","oddda","oedda","pddda","pedda","eedda","eeada","eeaea","eebda","eebea","eecda","eecea","eefda","eefea","eegda","eegea","eehda","eehea","eeida","eeiea","eejda","eejea","eekda","eekea","eelda","eelea","eemda","eemea","eenda","eenea","eeoda","eeoea","eepda","eepea","eeeea","ggggg","agggg","ahggg","bgggg","bhggg","cgggg","chggg","dgggg","dhggg","egggg","ehggg","fgggg","fhggg","igggg","ihggg","jgggg","jhggg","kgggg","khggg","lgggg","lhggg","mgggg","mhggg","ngggg","nhggg","ogggg","ohggg","pgggg","phggg","hhggg","hhagg","hhahg","hhbgg","hhbhg","hhcgg","hhchg","hhdgg","hhdhg","hhegg","hhehg","hhfgg","hhfhg","hhigg","hhihg","hhjgg","hhjhg","hhkgg","hhkhg","hhlgg","hhlhg","hhmgg","hhmhg","hhngg","hhnhg","hhogg","hhohg","hhpgg","hhphg","hhhhg","ahhhg","aihhg","bhhhg","bihhg","chhhg","cihhg","dhhhg","dihhg","ehhhg","eihhg","fhhhg","fihhg","ghhhg","gihhg","jhhhg","jihhg","khhhg","kihhg","lhhhg","lihhg","mhhhg","mihhg","nhhhg","nihhg","ohhhg","oihhg","phhhg","pihhg","iihhg","iiahg","iiaig","iibhg","iibig","iichg","iicig","iidhg","iidig","iiehg","iieig","iifhg","iifig","iighg","iigig","iijhg","iijig","iikhg","iikig","iilhg","iilig","iimhg","iimig","iinhg","iinig","iiohg","iioig","iiphg","iipig","iiiig","aiiig","ajiig","biiig","bjiig","ciiig","cjiig","diiig","djiig","eiiig","ejiig","fiiig","fjiig","giiig","gjiig","hiiig","hjiig","kiiig","kjiig","liiig","ljiig","miiig","mjiig","niiig","njiig","oiiig","ojiig","piiig","pjiig","jjiig","jjaig","jjajg","jjbig","jjbjg","jjcig","jjcjg","jjdig","jjdjg","jjeig","jjejg","jjfig","jjfjg","jjgig","jjgjg","jjhig","jjhjg","jjkig","jjkjg","jjlig","jjljg","jjmig","jjmjg","jjnig","jjnjg","jjoig","jjojg","jjpig","jjpjg","jjjjg","ajjjg","akjjg","bjjjg","bkjjg","cjjjg","ckjjg","djjjg","dkjjg","ejjjg","ekjjg","fjjjg","fkjjg","gjjjg","gkjjg","hjjjg","hkjjg","ijjjg","ikjjg","ljjjg","lkjjg","mjjjg","mkjjg","njjjg","nkjjg","ojjjg","okjjg","pjjjg","pkjjg","kkjjg","kkajg","kkakg","kkbjg","kkbkg","kkcjg","kkckg","kkdjg","kkdkg","kkejg","kkekg","kkfjg","kkfkg","kkgjg","kkgkg","kkhjg","kkhkg","kkijg","kkikg","kkljg","kklkg","kkmjg","kkmkg","kknjg","kknkg","kkojg","kkokg","kkpjg","kkpkg","kkkkg","ggggx","gggxx","ggxxx","gxxxx","xxxxx","xxxxy","xxxyy","xxyyy","xyyyy","yyyyy","yyyyw","yyyww","yywww","ywwww","wwwww","wwvww","wvvww","vvvww","vvvwz","avvwz","aavwz","aaawz","aaaaz"]
最快的算法
class Solution {
List<List<String>> ans = new ArrayList<>();
Map<String, Integer> wordToId = new HashMap<>();
Map<Integer, String> idToWord = new HashMap<>();
Map<Integer, List<Integer>> path = new HashMap<Integer, List<Integer>>();
Deque<String> list = new LinkedList<>();
int[] ne, e, h;
boolean[] vis;
int len, idx, start, end;
void add(int u, int v) {
e[++len] = v;
ne[len] = h[u];
h[u] = len;
}
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
int n = wordList.size();
ne = new int[20 * n];
e = new int[20 * n];
h = new int[20 * n];
vis = new boolean[10 * n];
if (!wordList.contains(beginWord)) wordList.add(beginWord);
if (!wordList.contains(endWord)) return ans;
for (int i = 0; i < wordList.size(); i++) addEdge(wordList.get(i));
Queue<Integer> q = new LinkedList<>();
start = wordToId.get(beginWord);
end = wordToId.get(endWord);
q.add(start);
while (!q.isEmpty()) {
int u = q.poll();
if (u == end) break;
if (vis[u]) continue;
vis[u] = true;
for (int j = h[u]; j != 0; j = ne[j]) {
int v = e[j];
if (vis[v]) continue;
if (!path.containsKey(v)) path.put(v, new ArrayList<>());
path.get(v).add(u);
q.add(v);
}
}
//从终点dfs搜索出路径
list.add(endWord);
dfs(end, 0);
return ans;
}
void dfs(int u, int level) {
if (u == start) {
//到达起点
ans.add(new ArrayList<>(list));
return;
}
List<Integer> p = path.get(u);
if (p == null) return;
for (int i = 0; i < p.size(); i++) {
int v = p.get(i);
if (level % 2 == 1) list.addFirst(idToWord.get(v));
dfs(v, level + 1);
if (level % 2 == 1) list.pollFirst();
}
}
void addEdge(String word) {
int u = idx;
char[] arr = word.toCharArray();
wordToId.put(word, idx);
idToWord.put(idx++, word);
for (int i = 0; i < arr.length; i++) {
char t = arr[i];
arr[i] = '*';
String vstr = new String(arr);
if (!wordToId.containsKey(vstr)) {
wordToId.put(vstr, idx);
idToWord.put(idx++, vstr);
}
int v = wordToId.get(vstr);
add(u, v);
add(v, u);
arr[i] = t;
}
}
}
他山之石1
于是,就去膜拜其他大佬的解法。
直观图
We just need to record all possible words that can connect from the beginning, level by level, until we hit the end at a level.
Then we will traverse backward from end via the words in the record and construct our final ways.
Remember: **we will not record paths, we record only nodes.**
我们只需要记录所有可能的单词,从头开始逐级连接,直到我们在一个级别结束。
然后我们将通过记录中的单词从末尾反向遍历并构建我们的最终方式。
请记住:我们不会记录路径,我们只记录节点。
解释
First, because we traverse level by level, so as soon as we see the end, that is the shortest distance (shortest path) we have from beginning.
This is the basic theorem of BFS in an unweighted graph: https://sneeit.com/graph/?tab=documentation#breath-first-search-in-graph
When we see the end, we know some of the nodes from previous level (which connect to the beginning because we traversed from there) are pointing to the end.
We just need to move backward, level by level then we could collect all paths to end from begin
首先,因为我们是逐层遍历,所以一看到终点,就是我们从起点到终点的最短距离(最短路径)。
这是未加权图中 BFS 的基本定理:https://sneeit.com/graph/?tab=documentation#breath-first-search-in-graph
当我们看到终点时,我们知道上一层的一些节点(连接到起点,因为我们从那里遍历)指向终点。
我们只需要逐级向后移动,然后我们就可以收集从开始到结束的所有路径
PS:第一次听说这个定理。
Why Other’s Solutions Get TLE 为何其他算法超时
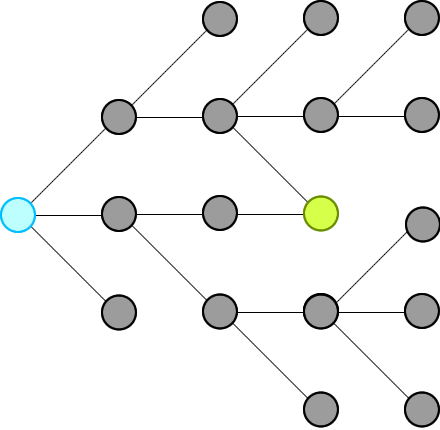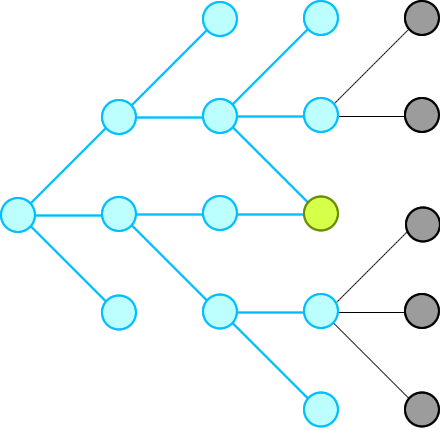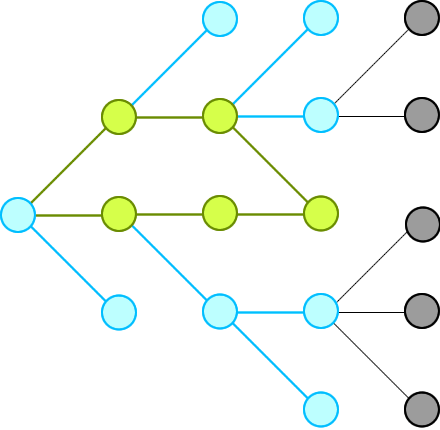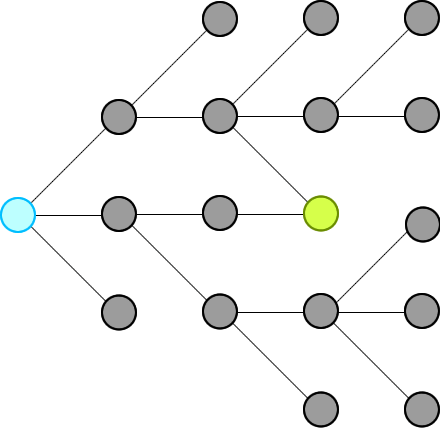
Because if there are some nodes point to a same node, their solutions keep computing the same path again and again due to they see those paths are different (from the beginning node). This is the weakness of recording paths, instead of nodes.
Check the red node in the following figure for more information:
因为如果有一些节点指向同一个节点,他们的解决方案会一次又一次地计算相同的路径,因为他们看到这些路径是不同的(从开始节点开始)。
这是记录路径而不是节点的弱点。
检查下图中的红色节点以获取更多信息:
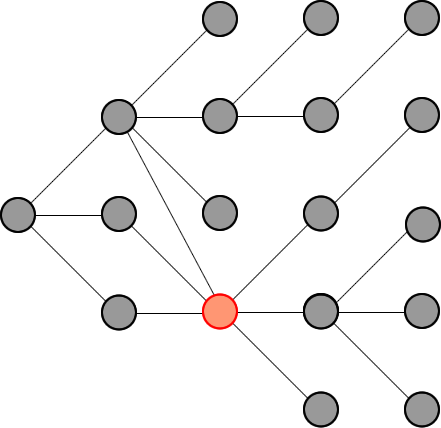
In summary:
Other solutions:
Store paths, so every node could be stored multiple times.
Compute the intersections in paths again and again
Paths that does not lead to end also be computed
My solution:
Store only nodes so every node is store exactly one time
Move backward to compute only the paths that can connect from begin to end
总之:
其他解决方案:
存储路径,因此每个节点都可以存储多次。
一次又一次地计算路径中的交叉点
不通向终点的路径也被计算
我的解决方案:
仅存储节点,因此每个节点都只存储一次
向后移动以仅计算可以从头到尾连接的路径
PS: 其实这里就是所谓的剪枝。剩下的就是要如何解决这 2 个问题了。
算法
Algorithm
Moving Forward: start from begin
Each level, find all connected nodes to the nodes of the current level in the record and add those to the record for the next level.
Delete node from wordList to prevent revisiting and forming cycles
Repeat the above steps until we reach end or we add no new nodes to the record for next level
Moving Backward: start from end
Do the same steps as moving forward but this time we will not record nodes but contruct our paths
Construct paths in reversing order to have paths from begin to end
前进:从头开始
每一层,在记录中找到所有连接到当前层节点的节点,并将它们添加到下一层的记录中。
从 wordList 中删除节点以防止重新访问和形成循环
重复上述步骤直到我们到达终点或者我们没有向下一级的记录添加新节点
向后移动:从结束开始
执行与前进相同的步骤,但这次我们不会记录节点,而是构建我们的路径
以相反的顺序构建路径,使路径从头到尾
实现
伪代码
// Pseudocode
function findLadders(beginWord, endWord, wordList) {
if (wordList.hasNo(endWord)) return []
wordList.delete(beginWord)
// move forward
queue = [beginWord]
paths = [] // 2D array
reached = false;
while (queue.length && !reached) {
paths.append(queue) // deep copy
// need static here to access only the nodes of this level
qlen = queue.length;
for (let i = 0; i < qlen && !reached; i++) {
from = queue.takeFirst()
forEach (to of wordList) {
if (isConnected(from, to)) {
if (to == endWord) {
reached = true
break // exit from the forEach
}
queue.push(to)
wordList.delete(to) // delete to preven a cycle
}
}
}
}
// can not reach the end eventually
if (!reached) return []
// move backward
answer = [[endWord]] // 2D array
for (level = paths.length - 1; level >= 0; level--) {
path = paths[level]
alen = answer.length
for (a = 0; a < alen; a++) {
p = answer.takeFirst()
last = p[0]
forEach (word of path) {
if (!isConnected(last, word)) {
answer.append([word, ...p])
}
}
}
}
return answer
}
// to check if two words can connect
function isConnected(a,b) {
c = 0
for (i = 0; i < a.length && c < 2; i++) {
if (a[i] !== b[i]) c++
}
return c == 1
}
java 实现
class Solution {
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
// boolean value indicate visited
Map<String, Boolean> wordDict = new HashMap<>();
for (String word : wordList) {
wordDict.put(word, false);
}
if (!wordDict.containsKey(endWord)) {
return new ArrayList<>();
}
Queue<String> q = new LinkedList<>();
// level of bfs
List<List<String>> levels = new ArrayList<>();
boolean reached = false;
wordDict.remove(beginWord);
q.offer(beginWord);
qLoop:
while (!q.isEmpty()) {
int qSize = q.size();
List<String> currentLevel = new ArrayList<>();
for (int i = 0; i < qSize; i++) {
String curr = q.poll();
currentLevel.add(curr);
if (curr.equals(endWord)) {
reached = true;
break qLoop;
}
for (String word : wordDict.keySet()) {
boolean visited = wordDict.get(word);
if (visited || !isConnected(word, curr)) continue;
wordDict.put(word, true);
q.offer(word);
}
}
levels.add(currentLevel);
}
if (!reached) {
return new ArrayList<>();
}
LinkedList<String> endPath = new LinkedList<>();
endPath.add(endWord);
List<List<String>> paths = new ArrayList<>();
paths.add(endPath);
for (int i = levels.size() - 1; i >= 0; i--) {
List<List<String>> tmpPaths = new ArrayList<>();
List<String> currentLevel = levels.get(i);
for (List<String> path : paths) {
String curr = path.get(0);
for (String word : currentLevel) {
if (!isConnected(word, curr)) continue;
LinkedList<String> newPath = new LinkedList<>(path);
newPath.addFirst(word);
tmpPaths.add(newPath);
}
}
paths = tmpPaths;
}
return paths;
}
private boolean isConnected(String a, String b) {
if (a.length() != b.length()) return false;
int diffCount = 0;
for (int i = 0; i < a.length() && diffCount < 2; i++) {
if (a.charAt(i) != b.charAt(i)) {
diffCount++;
}
}
return diffCount == 1;
}
}
他山之石2
该解决方案包含两个步骤 1 使用 BFS 构造图形。
2.使用DFS构建从头到尾的路径。
两种解决方案都在1s内获得AC。
第一步BFS相当重要。 我总结了三个技巧
-
用一个MAP来存储每个单词的min ladder,或者用一个SET来存储当前梯子中访问过的单词,当当前梯子完成后,将访问过的单词从未访问过的单词中删除。 这就是为什么我有两个类似的解决方案。
-
使用字符迭代来查找所有可能的路径。 不要将一个词与所有其他词进行比较,并检查它们是否仅相差一个字符。
-
一个词只允许插入队列一次。
java 实现
实现 1
public class Solution {
Map<String,List> map;
List<List> results;
public List<List> findLadders(String start, String end, Set dict) {
results= new ArrayList<List>();
if (dict.size() == 0)
return results;
int min=Integer.MAX_VALUE;
Queue<String> queue= new ArrayDeque<String>();
queue.add(start);
map = new HashMap<String,List<String>>();
Map<String,Integer> ladder = new HashMap<String,Integer>();
for (String string:dict)
ladder.put(string, Integer.MAX_VALUE);
ladder.put(start, 0);
dict.add(end);
//BFS: Dijisktra search
while (!queue.isEmpty()) {
String word = queue.poll();
int step = ladder.get(word)+1;//'step' indicates how many steps are needed to travel to one word.
if (step>min) break;
for (int i = 0; i < word.length(); i++){
StringBuilder builder = new StringBuilder(word);
for (char ch='a'; ch <= 'z'; ch++){
builder.setCharAt(i,ch);
String new_word=builder.toString();
if (ladder.containsKey(new_word)) {
if (step>ladder.get(new_word))//Check if it is the shortest path to one word.
continue;
else if (step<ladder.get(new_word)){
queue.add(new_word);
ladder.put(new_word, step);
}else;// It is a KEY line. If one word already appeared in one ladder,
// Do not insert the same word inside the queue twice. Otherwise it gets TLE.
if (map.containsKey(new_word)) //Build adjacent Graph
map.get(new_word).add(word);
else{
List<String> list= new LinkedList<String>();
list.add(word);
map.put(new_word,list);
//It is possible to write three lines in one:
//map.put(new_word,new LinkedList<String>(Arrays.asList(new String[]{word})));
//Which one is better?
}
if (new_word.equals(end))
min=step;
}//End if dict contains new_word
}//End:Iteration from 'a' to 'z'
}//End:Iteration from the first to the last
}//End While
//BackTracking
LinkedList<String> result = new LinkedList<String>();
backTrace(end,start,result);
return results;
}
private void backTrace(String word,String start,List<String> list){
if (word.equals(start)){
list.add(0,start);
results.add(new ArrayList<String>(list));
list.remove(0);
return;
}
list.add(0,word);
if (map.get(word)!=null)
for (String s:map.get(word))
backTrace(s,start,list);
list.remove(0);
}
}
实现方式 2
Another solution using two sets.
This is similar to the answer in the most viewed thread.
While I found my solution more readable and efficient.
public class Solution {
List<List<String>> results;
List<String> list;
Map<String,List<String>> map;
public List<List<String>> findLadders(String start, String end, Set<String> dict) {
results= new ArrayList<List<String>>();
if (dict.size() == 0)
return results;
int curr=1,next=0;
boolean found=false;
list = new LinkedList<String>();
map = new HashMap<String,List<String>>();
Queue<String> queue= new ArrayDeque<String>();
Set<String> unvisited = new HashSet<String>(dict);
Set<String> visited = new HashSet<String>();
queue.add(start);
unvisited.add(end);
unvisited.remove(start);
//BFS
while (!queue.isEmpty()) {
String word = queue.poll();
curr--;
for (int i = 0; i < word.length(); i++){
StringBuilder builder = new StringBuilder(word);
for (char ch='a'; ch <= 'z'; ch++){
builder.setCharAt(i,ch);
String new_word=builder.toString();
if (unvisited.contains(new_word)){
//Handle queue
if (visited.add(new_word)){//Key statement,Avoid Duplicate queue insertion
next++;
queue.add(new_word);
}
if (map.containsKey(new_word))//Build Adjacent Graph
map.get(new_word).add(word);
else{
List<String> l= new LinkedList<String>();
l.add(word);
map.put(new_word, l);
}
if (new_word.equals(end)&&!found) found=true;
}
}//End:Iteration from 'a' to 'z'
}//End:Iteration from the first to the last
if (curr==0){
if (found) break;
curr=next;
next=0;
unvisited.removeAll(visited);
visited.clear();
}
}//End While
backTrace(end,start);
return results;
}
private void backTrace(String word,String start){
if (word.equals(start)){
list.add(0,start);
results.add(new ArrayList<String>(list));
list.remove(0);
return;
}
list.add(0,word);
if (map.get(word)!=null)
for (String s:map.get(word))
backTrace(s,start);
list.remove(0);
}
}
TBC
感觉图这一块,自己还是不会。
BFS
DFS
还是需要多熟悉。
参考资料
https://leetcode.com/problems/word-ladder/solutions/1764371/a-very-highly-detailed-explanation/?orderBy=most_votes
https://leetcode.com/problems/word-ladder-ii/solutions/40475/my-concise-java-solution-based-on-bfs-and-dfs/?orderBy=most_votes
https://leetcode.com/problems/word-ladder-ii/solutions/40477/super-fast-java-solution-two-end-bfs/
https://leetcode.com/problems/word-ladder-ii/
https://leetcode.com/problems/word-ladder-ii/solutions/2424910/explanation-with-animation-accepted-without-tle/
https://leetcode.com/problems/word-ladder-ii/solutions/40447/share-two-similar-java-solution-that-accpted-by-oj/
https://leetcode.com/problems/word-ladder-ii/solutions/1211402/java-clean-bfs-dfs-solution-98-two-way-bfs-with-comments/?orderBy=most_votes&languageTags=java
https://leetcode.com/problems/word-ladder-ii/submissions/871819309/
