题目
给定一个整数 n,求以 1 … n 为节点组成的二叉搜索树有多少种?
示例:
输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
约定:1 <= n <= 19
第一感觉
第一眼看到这个题目,整个人都是懵的。
我是谁?我在哪里?我为什么而来?
无奈之下,只能去看下解析,这里整理下来,便于后续学习。
BST 的概念
很多解法都是直接上 DP 解法,不过我们还是从基础学起。
到底什么是 BST(二叉搜索树)?
其实这个概念非常简单,二叉树里每个节点都是一个爸爸,每个爸爸有两个儿子。
而二叉“搜索”树就是要满足一个额外的条件:所有左儿子的数字都比爸爸数字小,所有右儿子的数字都比爸爸数字大。
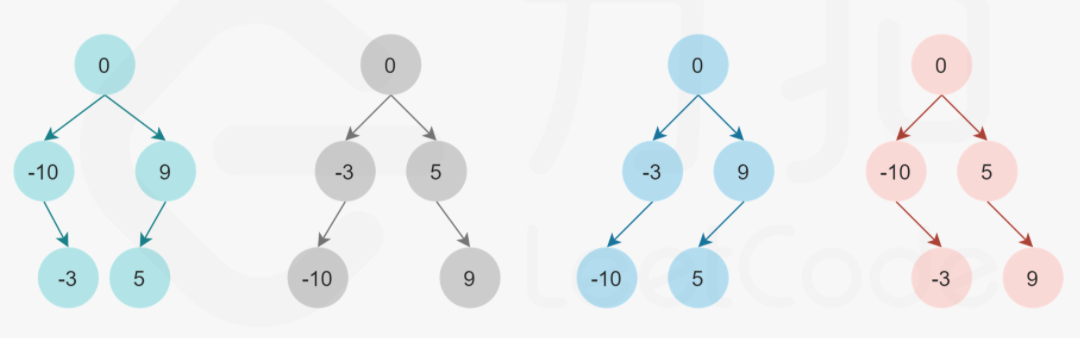
至于为什么叫二叉搜索树,实际上和二分查找法是一一对应的。
这种数据结构就是为了提升查询速度而生的,可以保证每次缩短一半的查询范围。
解题思路
由于 1,2…n 这个数列是递增的,所以我们从任意一个位置“提起”这课树,都满足二叉搜索树的这个条件:左边儿子数小于爸爸数,右边儿子数大于爸爸数 从 1,2,…n 数列构建搜索树,实际上只是一个不断细分的过程。
例子
例如,我要用 [1,2,3,4,5,6] 构建
首先,提起 “2” 作为树根,[1]为左子树,[3,4,5,6] 为右子树 现在就变成了一个更小的问题:如何用 [3,4,5,6] 构建搜索树?
比如,我们可以提起 “5” 作为树根,[3,4] 是左子树,[6] 是右子树 现在就变成了一个更更小的问题:如何用 [3,4] 构建搜索树?
那么这里就可以提起 “3” 作为树根,[4] 是右子树;或 “4” 作为树根,[3] 是左子树 可见 n=6 时的问题是可以不断拆分成更小的问题的
推广
假设 f(n)= 我们有 n 个数字时可以构建几种搜索树
我们可以很容易得知几个简单情况 f(0) = 1, f(1) = 1, f(2) = 2
(注:这里的 f(0) 可以理解为 =1 也可以理解为 =0,这个不重要,我们这里理解为 =1,即没有数字时只有一种情况,就是空的情况) 那 n=3 时呢?
我们来看 [1,2,3]
如果提起 1 作为树根,左边有f(0)种情况,右边 f(2) 种情况,左右搭配一共有 f(0)*f(2) 种情况
如果提起 2 作为树根,左边有f(1)种情况,右边 f(1) 种情况,左右搭配一共有 f(1)*f(1) 种情况
如果提起 3 作为树根,左边有f(2)种情况,右边 f(0) 种情况,左右搭配一共有 f(2)*f(0) 种情况
容易得知 f(3) = f(0)*f(2) + f(1)*f(1) + f(2)*f(0)
ps: 因为左右两边是独立的,所有的情况就是左子树的所有可能*右子树的所有可能。
同理,
f(4) = f(0)*f(3) + f(1)*f(2) + f(2)*f(1) + f(3)*f(0)
f(5) = f(0)*f(4) + f(1)*f(3) + f(2)*f(2) + f(3)*f(1) + f(4)*f(0)
找规律
其实分析到这里,这一题就变成了一道初中数学——找规律。
对于每一个 n,其式子都是有规律的:每一项两个 f() 的数字加起来都等于 n-1。 既然我们已知 f(0)=1, f(1)=1
那么就可以先算出 f(2),再算出 f(3),然后 f(4) 也可以算了…
计算过程中可以把这些存起来,方便随时使用
最后得到的 f(n) 就是我们需要的解了。
代码实现
java
实际上这题本质上还是一道 DP 问题。
public int numTrees(int n) {
int[] dp = new int[n+1];
// 初始化
dp[0] = 1;
dp[1] = 1;
// 遍历
for(int i = 2; i <= n; i++) {
int sum = 0;
for(int j = 0; j < i; j++) {
// 左边 * 右边
sum += dp[j] * dp[i-1-j];
}
dp[i] =sum ;
}
return dp[n];
}
效果:
Runtime: 0 ms, faster than 100.00% of Java online submissions for Unique Binary Search Trees.
Memory Usage: 35.8 MB, less than 39.07% of Java online submissions for Unique Binary Search Trees.
复杂度分析
时间复杂度:O(N^2) N 个数据,每一个节点有需要继续遍历 N 次。
空间复杂度: O(N)
数学的解法
还能更优吗?
一般而言,我们超越了 100% 的答案,也算是通过了。
不过如果要求是最优解的话,上面的答案,显然是远远不够的。
卡塔兰数 C_n
事实上我们在方法一中推导出的 G(n)函数的值在数学上被称为卡塔兰数 C_n。
卡塔兰数更便于计算的定义如下:
C_0 = 1;
C_n+1 = (2(2n+1) / n+2 ) * C_n
java 实现
那么上面的代码就可以如下实现:
public int numTrees(int n) {
// 提示:我们在这里需要用 long 类型防止计算过程中的溢出
long c = 1;
// 当然,针对 2 的乘法,还可以使用位运算进行优化。
for (int i = 0; i < n; ++i) {
c = c * 2 * (2 * i + 1) / (i + 2);
}
return (int) c;
}
效果:
Runtime: 0 ms, faster than 100.00% of Java online submissions for Unique Binary Search Trees.
Memory Usage: 35.7 MB, less than 52.56% of Java online submissions for Unique Binary Search Trees.
复杂度分析
时间复杂度 : O(n),其中 nn 表示二叉搜索树的节点个数。我们只需要循环遍历一次即可。
空间复杂度 : O(1)。我们只需要常数空间存放若干变量。
所以说,学好数学是多么的重要!
优化的尽头
问
那么问你,这就是最优解了吗?
只针对这一题,你还有更快的解法吗?
面向测试案例编程
这里要介绍一种非常赖皮,但是很有用的解法,那就是面向测试案例编程。
题目中 n 的数量实际上是固定的,所以答案是可以枚举的。
本质上就是我们先给出上面的算法,然后提前结算出所有的答案,然后利用查表法,节省计算的时间。
java 实现
int numTrees(int n) {
switch(n){
case 1: return 1;
case 2: return 2;
case 3: return 5;
case 4: return 14;
case 5: return 42;
case 6: return 132;
case 7: return 429;
case 8: return 1430;
case 9: return 4862;
case 10: return 16796;
case 11: return 58786;
case 12: return 208012;
case 13: return 742900;
case 14: return 2674440;
case 15: return 9694845;
case 16: return 35357670;
case 17: return 129644790;
case 18: return 477638700;
case 19: return 1767263190;
default: return 0;
}
}
效果:
Runtime: 0 ms, faster than 100.00% of Java online submissions for Unique Binary Search Trees.
Memory Usage: 35.4 MB, less than 90.45% of Java online submissions for Unique Binary Search Trees.
当然,严格而言,这已经不是算法了,所以实际面试过程中,一定要先给出前面的解法,最后给出这个解法。
也算是多出一种解题思路。
小结
希望本文对你有帮助,如果有其他想法的话,也可以评论区和大家分享哦。
各位极客的点赞收藏转发,是老马持续写作的最大动力!
参考资料
- 顺序查找
https://www.cnblogs.com/yw09041432/p/5908444.html
https://www.jb51.net/article/53863.htm
https://blog.csdn.net/jiandanokok/article/details/50517837
- 二分查找
https://www.cnblogs.com/ider/archive/2012/04/01/binary_search.html
