# 一、实验概览
lab3实现的是基于代价的查询优化器,以下是讲义给出的实验的大纲:
Recall that the main idea of a cost-based optimizer is to:
- Use statistics about tables to estimate “costs” of different
> query plans. Typically, the cost of a plan is related to the cardinalities(基数) of
> (number of tuples produced by) intermediate joins and selections, as well as the
> selectivity of filter and join predicates.
- Use these statistics to order joins and selections in an
> optimal way, and to select the best implementation for join
> algorithms from amongst several alternatives.
In this lab, you will implement code to perform both of these
functions.
我们可以使用表的统计数据去估计不同查询计划的代价。
通过这些统计信息,我们可以选择最佳的连接和选择顺序,从多个查询方案中选择一个最佳的计划去执行。
优化器结构概览:
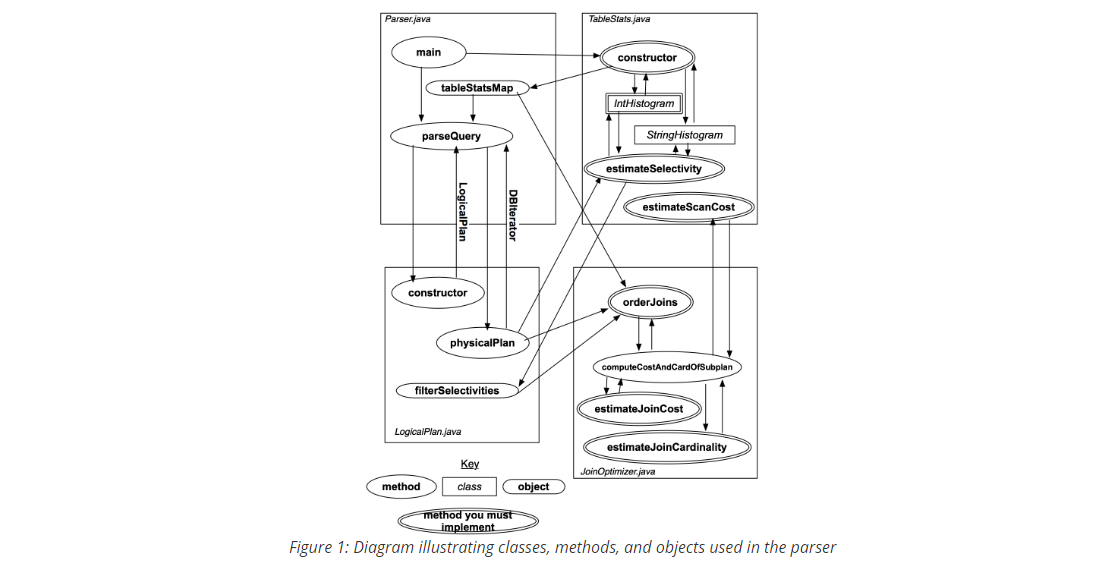
简单总结一下查询优化器的构成:
-
Parser.Java 在初始化时会收集并构造所有表格的统计信息(包括极值, 分桶直方图等等),并存到statsMap中。当有查询请求发送到Parser中时,会调用parseQuery方法去处理
-
parseQuery方法会把解析器解析后的结果去构造出一个LogicalPlan实例,然后调用LogicalPlan实例的physicalPlan方法, 构建一个物理执行计划(也即包含了各种执行算子),然后返回的是结果记录的迭代器,也就是我们在lab2中做的东西都会在physicalPlan中会被调用。
可以看到,lab2我们保证的是一般的SQL语句能够执行;
而在lab3,我们要考虑的事情是怎么让SQL执行得更快,最佳的连接的顺序是什么等待。
个人理解,总体的,lab3的查询优化应该分为两个阶段:
-
第一阶段:收集表的统计信息,有了统计信息我们才可以进行估计;
-
第二阶段:针对 logicalPlan, 生成各种 physicalPlan, 并根据统计信息进行估计每一种 Plan 的代价,找出最优的执行方案。
lab3共有4个exercise,前面两个exercise做的是第一阶段事情,后面两个exercise做的是第二阶段是事情。
除了上面信息,实验的文档outline部分还给出了很多十分有用的信息,告诉我们如何去统计数据,如何去计算代价等等,可以说是指导方针了。
二、Guideline
Exercise 1: IntHistogram.java
想要估计查询计划的代价,首先是得有统计数据。
那么数据是怎么从table中获取,以怎样的形式收集并统计呢?
这里用到了直方图。
简单来讲,一个直方图用于表示一个字段的统计信息,直方图将字段的值分为多个相同的区间,并统计每个区间的记录数,每个区间可以看做是一个桶,单个区间的范围大小看成桶的宽,记录数看成桶的宽,可以说是非常的形象:
这里采用了等宽直方图, 还由等深直方图
如果看不懂,可以看一下《数据库系统概念》里的图,帆船书里面的图会更容易懂一些。
一张人员信息表格,年龄字段的直方图如下:
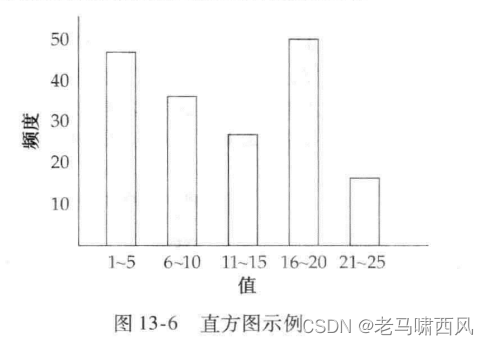
exercise1 要做的就是根据给定的数据字段去构造出这样的直方图,然后是根据直方图的统计信息去估算某个值的选择性(selectivity)。
下面是文档描述信息:
我们在这个实验只需要实现IntHistogram,而StringHistogram会将字符串转换为int类型然后调用IntHistogram。
首先,是构造器与属性部分。
构造器给出直方图的数据范围(最大值最小值),桶的数量。
有了这些信息,就可以构造出一个空的直方图。
具体实现也是一些很简单的数学计算:
private int maxVal;
private int minVal;
private int[] heights;
private int buckets;
private int totalTuples;
private int width;
private int lastBucketWidth;
public IntHistogram(int buckets, int min, int max) {
// some code goes here
this.minVal = min;
this.maxVal = max;
this.buckets = buckets;
this.heights = new int[buckets];
int total = max - min + 1;
this.width = Math.max(total / buckets, 1);
this.lastBucketWidth = total - (this.width * (buckets - 1));
this.totalTuples = 0;
}
然后就是构造直方图统计数据的过程,也很简单,以下是实现代码:
public void addValue(Integer v) {
// some code goes here
if (v < this.minVal || v > this.maxVal) {
return;
}
int bucketIndex = (v - this.minVal) / this.width;
if (bucketIndex >= this.buckets) {
return;
}
this.totalTuples++;
this.heights[bucketIndex]++;
}
接下来是这个 exercise 的大块头,根据直方图已有的统计信息,去计算进行某种运算时某个值表格记录的选择性。
这部分的资料在 outline 很详细的给出如何估计:
简单总结一下:
- 对于等值运算 f = const,我们要利用直方图估计一个等值表达式f = const的选择性,首先需要计算出包含该const值的桶,然后进行计算:
result = (height / width) / totalTuples
可以这样考虑, 我们假设一个桶内的数据是均匀分布的, 比如一个桶由20个记录, 宽为1-5, 那么 const = 3 的记录数就是 20 / 5 = 4,也即利用平均值来进行估算 而 (height / width) / totalTuples 就代表了 const = 3 的数据的在所有记录中的占比
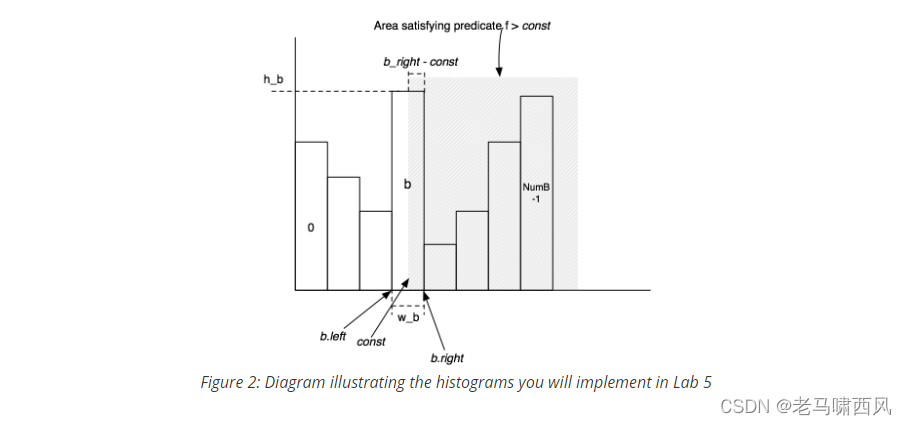
- 对于非等值运算,我们采用的也是同样的思想:
result = ((right - val) / bucketWidth) * (bucketTuples / totalTuples)
可以这样理解: (right - val) / bucketWidth) 代表了 f > const 在这个桶内的占比
(bucketTuples / totalTuples) 代表了这个桶在所有 tuples 的占比
二者相乘就是这个桶内 f > const 的占比
此外, 还要加上后续每一个桶的占比, 才是最终的 f > const 的结果
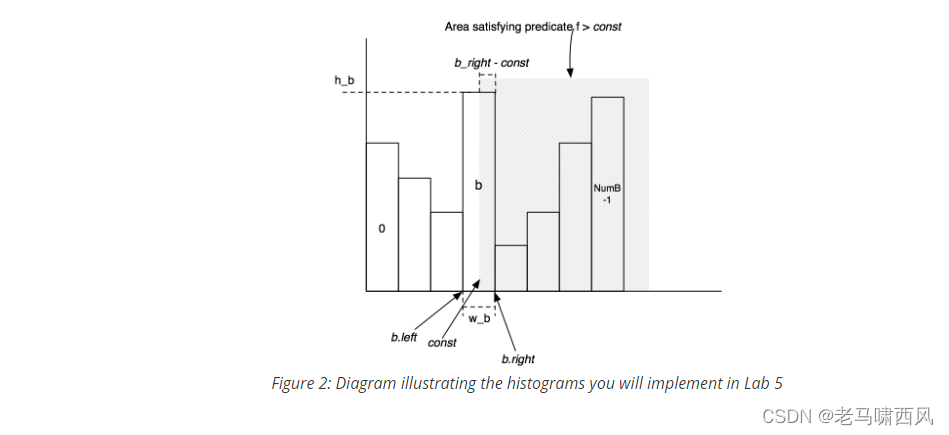
private double estimateGreater(int bucketIndex, int predicateValue, int bucketWidth) {
if (predicateValue < this.minVal) {
return 1.0;
}
if (predicateValue >= this.maxVal) {
return 0;
}
// As the lab3 doc, result = ((right - val) / bucketWidth) * (bucketTuples / totalTuples)
int bucketRight = bucketIndex * this.width + this.minVal;
double bucketRatio = (bucketRight - predicateValue) * 1.0 / bucketWidth;
double result = bucketRatio * (this.heights[bucketIndex] * 1.0 / this.totalTuples);
int sum = 0;
for (int i = bucketIndex + 1; i < this.buckets; i++) {
sum += this.heights[i];
}
return (sum * 1.0) / this.totalTuples + result;
}
private double estimateEqual(int bucketIndex, int predicateValue, int bucketWidth) {
if (predicateValue < this.minVal || predicateValue > this.maxVal) {
return 0;
}
// As the lab3 doc, result = (bucketHeight / bucketWidth) / totalTuples
double result = this.heights[bucketIndex];
result = result / bucketWidth;
result = result / this.totalTuples;
return result;
}
public double estimateSelectivity(Predicate.Op op, Integer v) {
final int bucketIndex = Math.min((v - this.minVal) / this.width, this.buckets - 1);
final int bucketWidth = bucketIndex < this.buckets - 1 ? this.width : this.lastBucketWidth;
double ans;
switch (op) {
case GREATER_THAN:
ans = estimateGreater(bucketIndex, v, bucketWidth);
break;
case EQUALS:
ans = estimateEqual(bucketIndex, v, bucketWidth);
break;
case LESS_THAN:
ans = 1.0 - estimateGreater(bucketIndex, v, bucketWidth) - estimateEqual(bucketIndex, v, bucketWidth);
break;
case LESS_THAN_OR_EQ:
ans = 1.0 - estimateGreater(bucketIndex, v, bucketWidth);
break;
case GREATER_THAN_OR_EQ:
ans = estimateEqual(bucketIndex, v, bucketWidth) + estimateGreater(bucketIndex, v, bucketWidth);
break;
case NOT_EQUALS:
ans = 1.0 - estimateEqual(bucketIndex, v, bucketWidth);
break;
default:
return -1;
}
return ans;
}
Exercise 2: TableStats.java
代码实现
exercise2要做的是根据给定的tableid,扫描出所有记录,并对每一个字段建立一个直方图。
下面是outline给出的指导方案:
简单总结一下:
-
扫描全表,把这个表每个字段的值给取出来, 对应函数 fetchFieldValues()
-
对于每个字段, 构建 histogram
要做的就是上面这两件事,然后就是写代码过测试了:
// FieldId -> histogram (String or Integer)
private final Map<Integer, Histogram> histogramMap;
private int totalTuples;
private int totalPages;
private int tableId;
private int ioCostPerPage;
private TupleDesc td;
构造器:
public TableStats(int tableid, int ioCostPerPage) {
this.ioCostPerPage = ioCostPerPage;
this.tableId = tableid;
this.histogramMap = new HashMap<>();
this.totalTuples = 0;
final HeapFile table = (HeapFile) Database.getCatalog().getDatabaseFile(tableid);
this.totalPages = table.numPages();
this.td = table.getTupleDesc();
// Build histogram for every field
final Map<Integer, ArrayList> fieldValues = fetchFieldValues(tableId);
for (final int fieldId : fieldValues.keySet()) {
if (td.getFieldType(fieldId) == Type.INT_TYPE) {
final List<Integer> values = (ArrayList<Integer>) fieldValues.get(fieldId);
final int minVal = Collections.min(values);
final int maxVal = Collections.max(values);
final IntHistogram histogram = new IntHistogram(NUM_HIST_BINS, minVal, maxVal);
for (final Integer v : values) {
histogram.addValue(v);
}
this.histogramMap.put(fieldId, histogram);
} else {
final List<String> values = (ArrayList<String>) fieldValues.get(fieldId);
final StringHistogram histogram = new StringHistogram(NUM_HIST_BINS);
for (final String v : values) {
histogram.addValue(v);
}
this.histogramMap.put(fieldId, histogram);
}
}
}
其中 fetchFieldValues 如下:
实现也比较简单,就是遍历所有的行。然后把所有的数据,按照列统计起来。
这里其实可以发现一个有趣的地方,那就是列式数据库,恰好可以省去这一步。
key: 列的下标 value: 列表内容
// Fetch table field's values by seqScan
private Map<Integer, ArrayList> fetchFieldValues(final int tableId) {
final Map<Integer, ArrayList> fieldValueMap = new HashMap<>();
for (int i = 0; i < td.numFields(); i++) {
if (td.getFieldType(i) == Type.INT_TYPE) {
fieldValueMap.put(i, new ArrayList<Integer>());
} else {
fieldValueMap.put(i, new ArrayList<String>());
}
}
final SeqScan seqScan = new SeqScan(new TransactionId(), tableId);
try {
seqScan.open();
while (seqScan.hasNext()) {
this.totalTuples++;
final Tuple next = seqScan.next();
for (int i = 0; i < td.numFields(); i++) {
final Field field = next.getField(i);
switch (field.getType()) {
case INT_TYPE: {
final int value = ((IntField) field).getValue();
fieldValueMap.get(i).add(value);
break;
}
case STRING_TYPE: {
final String value = ((StringField) field).getValue();
if (!Objects.equals(value, "")) {
fieldValueMap.get(i).add(value);
}
break;
}
}
}
}
} catch (Exception e) {
e.printStackTrace();
}
return fieldValueMap;
}
计算IO成本:
public double estimateScanCost() {
return numPages * ioCostPerPage;
}
根据选择性因子估计结果的记录数:
public int estimateTableCardinality(double selectivityFactor) {
return (int) (numTuples * selectivityFactor);
}
最后是估计某个字段的选择性,也是调用exercise1写的估计某个值的选择性那些东西:
public double estimateSelectivity(int field, Predicate.Op op, Field constant) {
if (this.histogramMap.containsKey(field)) {
switch (this.td.getFieldType(field)) {
case INT_TYPE: {
final IntHistogram histogram = (IntHistogram) this.histogramMap.get(field);
return histogram.estimateSelectivity(op, ((IntField) constant).getValue());
}
case STRING_TYPE: {
final StringHistogram histogram = (StringHistogram) this.histogramMap.get(field);
return histogram.estimateSelectivity(op, ((StringField) constant).getValue());
}
}
}
return 0.0;
}
Exercise 3: Join Cost Estimation
exercise3要做的是估计连接查询的代价,以下是讲义:
其实这应该是四个exercise最容易的一个,就是看懂了连接查询的公式,然后写一下就好了,以下是公式:
scancost(t1) + scancost(t2) + joincost(t1 join t2) + scancost(t3) + joincost((t1 join t2) join t3) +
这里提一下基于成本的估计。
一般查询的成本分为I/O成本和CPU成本,I/O成本就是我们扫描表获取记录时,需要发生磁盘I/O,产生的时间成本为I/O成本;而有了记录,我们需要判断这些记录符不符合查询的条件,这需要CPU去做,其中产生的时间就是CPU成本。
对于连接查询来说,以两表连接为例,首先需要扫描一张表然后过滤出一些记录,然后把过滤完的记录,每一条都去与第二张表进行匹配,这里第一张表称为驱动表t1,第二张表称为被驱动表t2。
在两表连接中,驱动表只需要扫描一次,然后产生card1条记录,而被驱动表则需要扫描card1次,这是总的IO成本;然后假设t2表有card2条记录,则产生的CPU成本应该为 card1 * card2。
所有总成本应该为:
t1的IO成本 + t1的记录数*t2的IO成本 (I/O成本) +t1的记录数*t2的记录数(CPU成本)
当然,实际的数据库去计算这些成本,都会有一些参数去调节,但总体的公式就是这样。
根据公式写出来的代码:
public double estimateJoinCost(LogicalJoinNode j, int card1, int card2, double cost1, double cost2) {
if (j instanceof LogicalSubplanJoinNode) {
// A LogicalSubplanJoinNode represents a subquery.
// You do not need to implement proper support for these for Lab 3.
return card1 + cost1 + cost2;
} else {
// Insert your code here.
// HINT: You may need to use the variable "j" if you implemented
// a join algorithm that's more complicated than a basic
// nested-loops join.
final double IoCost = cost1 + card1 * cost2;
final double CpuCost = card1 * card2;
return IoCost + CpuCost;
}
}
做完这个之后,该exercise的另一个任务就是估计连接产生的基数(cardinality),也就是产生结果的记录数。
简单总结一下:
-
如果其中一个是非主键, 我们选择非主键的 card 作为 joinCard
-
如果两个都是非主键, 我们选择 最大的 card 作为 joinCard
-
如果两个都是主键, 我们选择最小的 card 作为 joinCard
为什么呢????????
有了上面的理论基础,就可以写出代码了:
public static int estimateTableJoinCardinality(Predicate.Op joinOp, String table1Alias, String table2Alias,
String field1PureName, String field2PureName, int card1, int card2,
boolean t1pkey, boolean t2pkey, Map<String, TableStats> stats,
Map<String, Integer> tableAliasToId) {
/**
* * For equality joins, when one of the attributes is a primary key, the number of tuples produced by the join cannot
* be larger than the cardinality of the non-primary key attribute.
*
* * For equality joins when there is no primary key, it's hard to say much about what the size of the output
* is -- it could be the size of the product of the cardinalities of the tables (if both tables have the
* same value for all tuples) -- or it could be 0. It's fine to make up a simple heuristic (say,
* the size of the larger of the two tables).
*
* * For range scans, it is similarly hard to say anything accurate about sizes.
* The size of the output should be proportional to
* the sizes of the inputs. It is fine to assume that a fixed fraction
* of the cross-product is emitted by range scans (say, 30%). In general, the cost of a range
* join should be larger than the cost of a non-primary key equality join of two tables
* of the same size.
*/
int card = 1;
if (t1pkey && t2pkey) {
card = Math.min(card1, card2);
} else if (!t1pkey && !t2pkey) {
card = Math.max(card1, card2);
} else {
card = t1pkey ? card2 : card1;
}
switch (joinOp) {
case EQUALS: {
break;
}
case NOT_EQUALS: {
card = card1 * card2 - card;
break;
}
default: {
card = card1 * card2 / 3;
}
}
return card <= 0 ? 1 : card;
}
Exercise 4: Join Ordering
exercise3我们完成了连接查询的成本估计与基数估计,而exercise4我们要做的是根据在多表连接的情况下,去选择一个最优的连接顺序,来实现对连接查询的优化。
有了这个连接顺序就可以生成执行计划了。
总体的思想是列举出所有的连接顺序,计算出每种连接顺序的代价,然后选择代价最小的连接顺序去执行。
但是,如何列举是个问题。
举个例子,对于两表连接,连接顺序有2 * 1种可能;对于三表连接,有3 * 2 * 1 = 6种可能。
可以发现,按照枚举的方式去弄,有n!种方案。当n = 7时,方案数有655280种;
当n = 10时,方案数可以达到176亿。
可以看到,这个缺点特别明显,就是当连接的表数一多,我们的方案数回很多,时间复杂度很高。
所以本实验采用的是一种基于动态规划的查询计划生成。
动态规划的思想, 相信大家都有所了解, 也即先将低纬度的给计算好, 然后让高纬度基于低纬度进行计算, 在本次实验中,
我们只关心 left-deep-tree
举个例子, 假设我们有四个表, 分别是: emp, dept, hobby, hobbies
我们想执行这个 sql 语句:
select xx from emp, dept, hobby, hobbies
where
hobbies.c1 = hobby.c0 and
emp.c1 = dept.c0 and
emp.c2 = hobbies.c0
如何计算这三个连接的顺序呢?
假设利用 node1 代表 hobbies.c1 = hobby.c0
node2 代表 emp.c1 = dept.c0
node3 代表 emp.c2 = hobbies.c0
-
第一步: 先计算 1 个 joinNode 的执行代价, 也即 sql 中的 hobbies join hobby, emp join dept …., 并将这三个代价保存到一个 costmap 中 -»> node1->cost , node2 -> cost, node3->cost
-
第二步, 计算 2 个 joinNode 的最优执行代价:
- 生成2个 joinNode 的不同顺序: (node1, node2), (node1, node3), (node2, node3) 共三种顺序
- 其中, 去除 (node1, node2), 因为这两个 node 没有交集, 也即不存在一个表, 同时出现在两个 node 中
- 分别计算 (node1, node3), (node2, node3) 的最优执行计划
- 以 (node1, node3) 为例, 我们可以选择让 (hobbies join hobby) join emp, 也可以选择让 (emp join hobbies) join hobby, 选择的依据就是哪个 cost 比较小 (这里可能不好理解, 因为多表join, 我们考虑的是 left-deep-tree, 也即是前面的 join 执行完后, 再和第三个表 join)
- 这一步之后, costmap就有了 (node1, node3) -> cost, (node2, node3) -> cost
- 同时, 还可以他们的最优执行顺序 planMap, 比如 (node1, node3) 的顺序可能是 (node3, node1)
-
第三步, 计算 3 个 joinNode 的最优执行计划
- 步骤和 第二步类似, 也是让两个 node 先 join, 再join 第三个 node
下面是实验讲义给出的动态规划法伪代码:
j = set of join nodes
for (i in 1...|j|):
for s in {all length i subsets of j}
bestPlan = {}
for s' in {all length d-1 subsets of s}
subplan = optjoin(s')
plan = best way to join (s-s') to subplan
if (cost(plan) < cost(bestPlan))
bestPlan = plan
optjoin(s) = bestPlan
return optjoin(j)
java 实现:
public List<LogicalJoinNode> orderJoins(Map<String, TableStats> stats, Map<String, Double> filterSelectivities,
boolean explain) throws ParsingException {
final PlanCache pc = new PlanCache();
CostCard costCard = null;
for (int i = 1; i <= this.joins.size(); i++) {
// 生成 size = i 的子集, 可以利用回溯算法来做
final Set<Set<LogicalJoinNode>> subsets = enumerateSubsets(this.joins, i);
for (final Set<LogicalJoinNode> subPlan : subsets) {
double bestCost = Double.MAX_VALUE;
for (final LogicalJoinNode removeNode : subPlan) {
// 尝试将这个子集中的一个 node 从该子集中去除, 然后子集中剩下的 joinNode 进行 join, 估算代价
// 比如, node1 join node2 join node3
// 我们去除了 node1 ,
// 然后估算 (node2 join node3) join node1 和 node1 join (node2 join node3), 这两种哪个代价比较小, 而 (node2 join node3) 我们已经在之前的遍历中计算好了
final CostCard cc = computeCostAndCardOfSubplan(stats, filterSelectivities, removeNode, subPlan,
bestCost, pc);
if (cc != null) {
bestCost = cc.cost;
costCard = cc;
}
}
// 保存该子集的最优执行计划
if (bestCost != Double.MAX_VALUE) {
pc.addPlan(subPlan, bestCost, costCard.card, costCard.plan);
}
}
}
if (costCard != null) {
return costCard.plan;
} else {
return joins;
}
}
computeCostAndCardOfSubplan 的逻辑如下:
这个函数的目的是为了计算处 card1, card2, cost1, cost2, 并通过这四个参数计算 join cost
举个例子, 如果 joinSet = (node1, node2, node3), removeNode = node3
-
首先构建一个 news, 去除了 removeNode, news = (node1, node2)
-
根据 News, 获取之前已经计算好的 bestPlan -> 也即顺序可能是 (node2 join node1)
-
如果 removeNode 的 table1 包含在 news 中, 那么计算的流程就是 (node2 join node1) join node3
-
card1 = news.card, cost1 = news.bestCost
-
card2 = table2.card, cost2 = table2.cost
-
-
同理, 如果 table2 包含在 news 中, 计算流程就是 node3 join (node2 join node1)
private CostCard computeCostAndCardOfSubplan(Map<String, TableStats> stats,
Map<String, Double> filterSelectivities, LogicalJoinNode joinToRemove,
Set<LogicalJoinNode> joinSet, double bestCostSoFar, PlanCache pc) throws ParsingException {
LogicalJoinNode j = joinToRemove;
List<LogicalJoinNode> prevBest;
if (this.p.getTableId(j.t1Alias) == null)
throw new ParsingException("Unknown table " + j.t1Alias);
if (this.p.getTableId(j.t2Alias) == null)
throw new ParsingException("Unknown table " + j.t2Alias);
String table1Name = Database.getCatalog().getTableName(this.p.getTableId(j.t1Alias));
String table2Name = Database.getCatalog().getTableName(this.p.getTableId(j.t2Alias));
String table1Alias = j.t1Alias;
String table2Alias = j.t2Alias;
// 构建子集, 去除 removeNode
Set<LogicalJoinNode> news = new HashSet<>(joinSet);
news.remove(j);
double t1cost, t2cost;
int t1card, t2card;
boolean leftPkey, rightPkey;
if (news.isEmpty()) { // base case -- both are base relations
// 如果news 为空 , 说明是 base case, 我们只需要计算 removeNode 的代价就可以了
prevBest = new ArrayList<>();
t1cost = stats.get(table1Name).estimateScanCost();
t1card = stats.get(table1Name).estimateTableCardinality(filterSelectivities.get(j.t1Alias));
leftPkey = isPkey(j.t1Alias, j.f1PureName);
t2cost = table2Alias == null ? 0 : stats.get(table2Name).estimateScanCost();
t2card = table2Alias == null ? 0 : stats.get(table2Name).estimateTableCardinality(
filterSelectivities.get(j.t2Alias));
rightPkey = table2Alias != null && isPkey(table2Alias, j.f2PureName);
} else {
// 如果不为空, 先取出 news 的最优执行计划, 包括执行顺序和代价
prevBest = pc.getOrder(news);
// possible that we have not cached an answer, if subset
// includes a cross product
if (prevBest == null) {
return null;
}
double prevBestCost = pc.getCost(news);
int bestCard = pc.getCard(news);
// 如果 removeNode 的 left 包含在 prevBest 中
// 那么 card1 = news 的 bestCard
if (doesJoin(prevBest, table1Alias)) { // j.t1 is in prevBest
t1cost = prevBestCost; // left side just has cost of whatever
// left
// subtree is
t1card = bestCard;
leftPkey = hasPkey(prevBest);
t2cost = j.t2Alias == null ? 0 : stats.get(table2Name).estimateScanCost();
t2card = j.t2Alias == null ? 0 : stats.get(table2Name).estimateTableCardinality(
filterSelectivities.get(j.t2Alias));
rightPkey = j.t2Alias != null && isPkey(j.t2Alias, j.f2PureName);
} else if (doesJoin(prevBest, j.t2Alias)) { // j.t2 is in prevbest
// (both
// shouldn't be)
t2cost = prevBestCost; // left side just has cost of whatever
// left
// subtree is
t2card = bestCard;
rightPkey = hasPkey(prevBest);
t1cost = stats.get(table1Name).estimateScanCost();
t1card = stats.get(table1Name).estimateTableCardinality(filterSelectivities.get(j.t1Alias));
leftPkey = isPkey(j.t1Alias, j.f1PureName);
} else {
// don't consider this plan if one of j.t1 or j.t2
// isn't a table joined in prevBest (cross product)
return null;
}
}
// 计算 join 代价
double cost1 = estimateJoinCost(j, t1card, t2card, t1cost, t2cost);
LogicalJoinNode j2 = j.swapInnerOuter();
double cost2 = estimateJoinCost(j2, t2card, t1card, t2cost, t1cost);
if (cost2 < cost1) {
boolean tmp;
j = j2;
cost1 = cost2;
tmp = rightPkey;
rightPkey = leftPkey;
leftPkey = tmp;
}
if (cost1 >= bestCostSoFar)
return null;
CostCard cc = new CostCard();
cc.card = estimateJoinCardinality(j, t1card, t2card, leftPkey, rightPkey, stats);
cc.cost = cost1;
cc.plan = new ArrayList<>(prevBest);
cc.plan.add(j); // prevbest is left -- add new join to end
return cc;
}
我们可以对比一下优化前后提高的速度。优化前默认的连接顺序:耗时5s645ms
优化后选择了最佳的连接顺序:耗时1s673ms
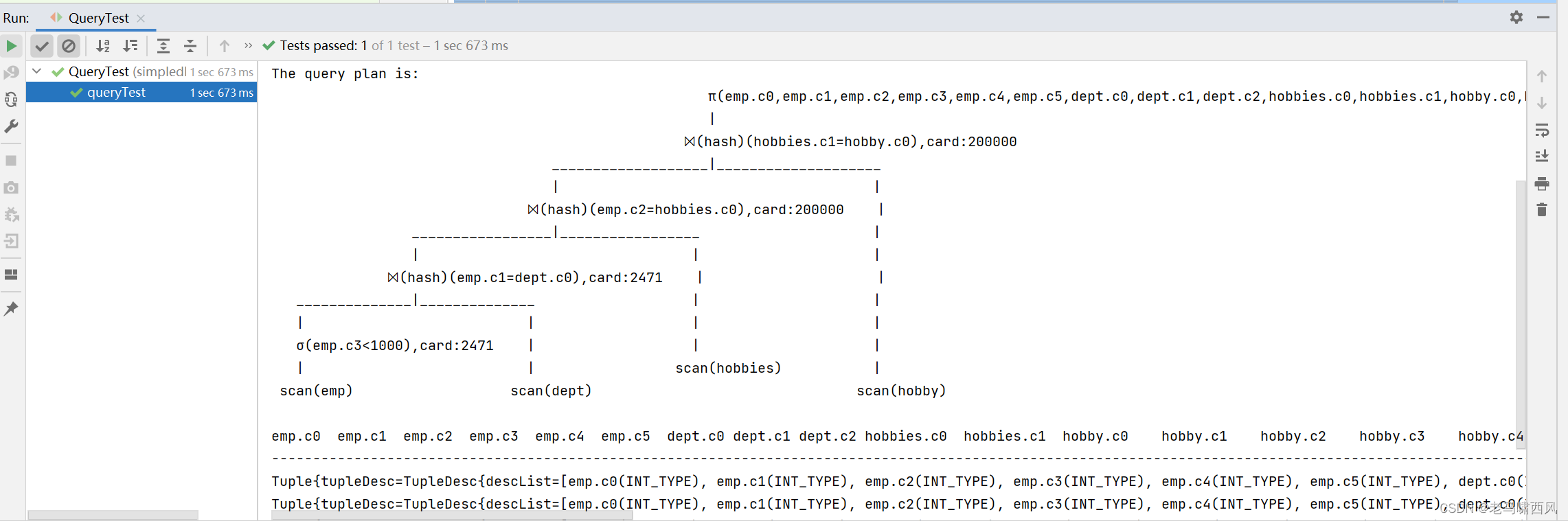
可以看到,速度快了三倍。
可见查询优化是多么重要。
参考资料
https://github.com/CreatorsStack/CreatorDB/blob/master/document/lab2-resolve.md
