DFS 什么是深度优先搜索?
深度优先搜索是用来遍历或搜索树和图数据结构的算法,它是可以从任意跟节点开始,选择一条路径走到底,并通过回溯来访问所有节点的算法。
简单来说就是通过选择一条道路走到无路可走的时候回退到上一个岔路口,并标记这条路已走过,选择另外一条道路继续走,直到走遍每一条路。
DFS 深度优先搜索的思想
DFS 思修基于递归思想,通过递归的形式来缩小问题规模,把一件事分割成若干个相同的小事,逐步完成。
深度优先搜索的步骤分为 1.递归下去 2.回溯上来。
顾名思义,深度优先,则是以深度为准则,先一条路走到底,直到达到目标。这里称之为递归下去。
否则既没有达到目标又无路可走了,那么则退回到上一步的状态,走其他路。这便是回溯上来。
DFS 有两个重要标志,也就是两个重要数组,一个是标记数组,标记该点是否被访问过,一个用来把该点放入数组,两个点是相辅相承的,通过放入一个起点,并标记起始点,然后依次搜索附近所有能访问的结点,用递归走到下一个点,重复这个步骤,直到走到目标点或是走完全图。
时间复杂度:
在深度优先搜索算法中,每条边最多会被访问两次,一次是遍历,一次是回退。
所以,深度优先搜索的时间复杂度为 O(E)
模板
void dfs()//参数用来表示状态
{
if(到达终点状态)
{
...//根据题意来添加
return;
}
if(越界或者是不符合法状态)//剪枝
return;
for(扩展方式)
{
if(扩展方式所达到状态合法)
{
....//根据题意来添加
标记;
dfs();
修改(剪枝);
(还原标记);
//是否还原标记根据题意
//如果加上(还原标记)就是 回溯法
}
}
}
剪枝
深度优先搜索会遍历万每一种可能的情况,因此往往解决问题时会耗费大量时间,但是可以通过省去一些越界和不合法的状态节省时间,这个省略的步骤被称为剪枝。
核心流程
深度优先搜索的过程类似于树的先序遍历,首先从例子中体会深度优先搜索。
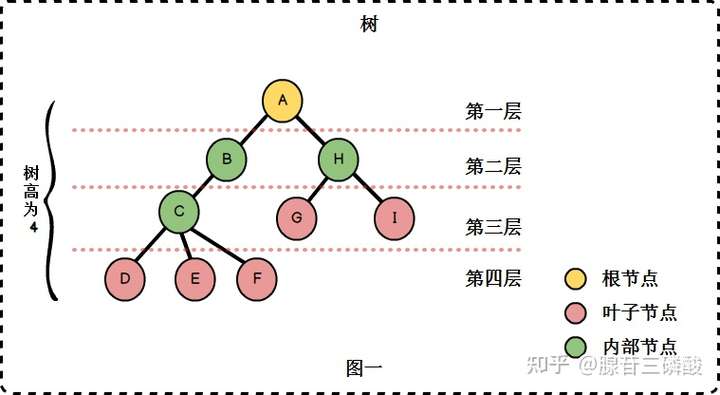
例如图 1 是一个无向图,采用深度优先算法遍历这个图的过程为:

-
首先任意找一个未被遍历过的顶点,例如从 V1 开始,由于 V1 率先访问过了,所以,需要标记 V1 的状态为访问过;
-
然后遍历 V1 的邻接点,例如访问 V2 ,并做标记,然后访问 V2 的邻接点,例如 V4 (做标记),然后 V8 ,然后 V5 ;
-
当继续遍历 V5 的邻接点时,根据之前做的标记显示,所有邻接点都被访问过了。此时,从 V5 回退到 V8 ,看 V8 是否有未被访问过的邻接点,如果没有,继续回退到 V4 , V2 , V1 ;
-
通过查看 V1 ,找到一个未被访问过的顶点 V3 ,继续遍历,然后访问 V3 邻接点 V6 ,然后 V7 ;
-
由于 V7 没有未被访问的邻接点,所有回退到 V6 ,继续回退至 V3 ,最后到达 V1 ,发现没有未被访问的;
-
最后一步需要判断是否所有顶点都被访问,如果还有没被访问的,以未被访问的顶点为第一个顶点,继续依照上边的方式进行遍历。
根据上边的过程,可以得到图 1 通过深度优先搜索获得的顶点的遍历次序为:
V1 -> V2 -> V4 -> V8 -> V5 -> V3 -> V6 -> V7
所谓深度优先搜索,是从图中的一个顶点出发,每次遍历当前访问顶点的临界点,一直到访问的顶点没有未被访问过的临界点为止。
然后采用依次回退的方式,查看来的路上每一个顶点是否有其它未被访问的临界点。
访问完成后,判断图中的顶点是否已经全部遍历完成,如果没有,以未访问的顶点为起始点,重复上述过程。
深度优先搜索是一个不断回溯的过程。
主要解决问题
深度优先遍历(Depth First Search, 简称 DFS) 与广度优先遍历(Breath First Search)是图论中两种非常重要的算法,生产上广泛用于拓扑排序,寻路(走迷宫),搜索引擎,爬虫等,也频繁出现在 leetcode,高频面试题中。
数字型
比如数字的全排列问题
地图型
广度优先搜索
广度优先搜索类似于树的层次遍历。
从图中的某一顶点出发,遍历每一个顶点时,依次遍历其所有的邻接点,然后再从这些邻接点出发,同样依次访问它们的邻接点。按照此过程,直到图中所有被访问过的顶点的邻接点都被访问到。
最后还需要做的操作就是查看图中是否存在尚未被访问的顶点,若有,则以该顶点为起始点,重复上述遍历的过程。
还拿图 1 中的无向图为例,假设 V1 作为起始点,遍历其所有的邻接点 V2 和 V3 ,以 V2 为起始点,访问邻接点 V4 和 V5 ,以 V3 为起始点,访问邻接点 V6 、 V7 ,以 V4 为起始点访问 V8 ,以 V5 为起始点,由于 V5 所有的起始点已经全部被访问,所有直接略过, V6 和 V7 也是如此。
以 V1 为起始点的遍历过程结束后,判断图中是否还有未被访问的点,由于图 1 中没有了,所以整个图遍历结束。
遍历顶点的顺序为:
V1 -> V2 -> v3 -> V4 -> V5 -> V6 -> V7 -> V8
133-克隆图
看了上面的解释,你可能感觉很简单,也可能感觉很疑惑。
我们还是直接解决一个问题,体验一下 DFS 和 BFS。
题目
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
class Node {
public int val;
public List<Node> neighbors;
}
测试用例格式:
简单起见,每个节点的值都和它的索引相同。
例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。
你必须将 给定节点的拷贝 作为对克隆图的引用返回。
- 示例 1:
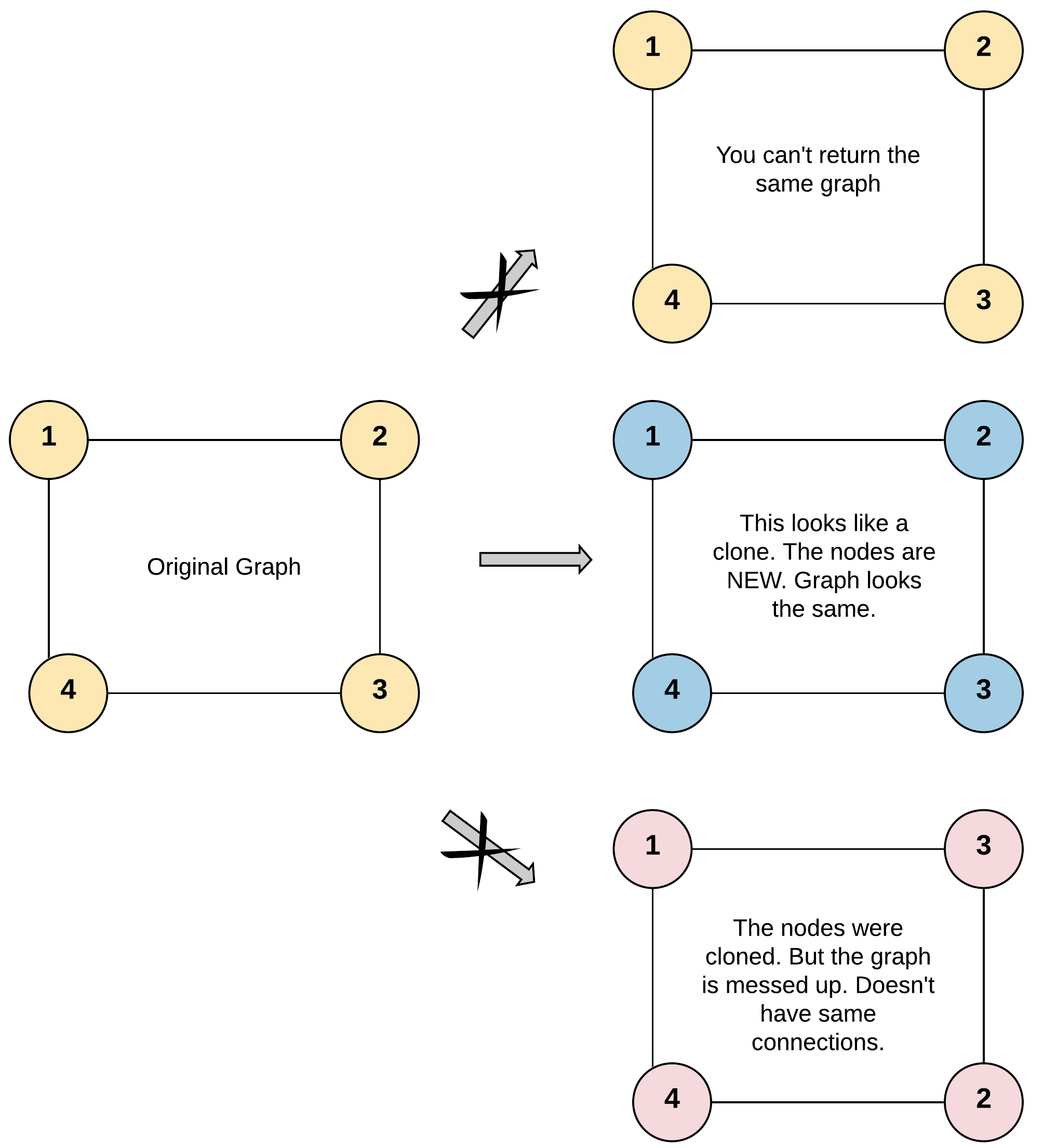
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。
提示:
-
节点数不超过 100 。
-
每个节点值 Node.val 都是唯一的,1 <= Node.val <= 100。
-
无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
-
由于图是无向的,如果节点 p 是节点 q 的邻居,那么节点 q 也必须是节点 p 的邻居。
-
图是连通图,你可以从给定节点访问到所有节点。
其中 Node 定义如下:
class Node {
public int val;
public List<Node> neighbors;
public Node() {
val = 0;
neighbors = new ArrayList<Node>();
}
public Node(int _val) {
val = _val;
neighbors = new ArrayList<Node>();
}
public Node(int _val, ArrayList<Node> _neighbors) {
val = _val;
neighbors = _neighbors;
}
}
思路1-DFS 深度优先遍历
这一题的本质上还是在考量大家对于图遍历的掌握情况。
主要有几个问题需要考虑:
(1)DFS 深度优先遍历,如何记录被访问过的节点?
(2)如何存放拷贝后的节点
(3)如何深度拷贝
针对问题1,我们可以使用一个 boolean 数组,每一个下标初始化为 false,访问完之后,设置为 true。
针对问题2,我们可以使用 HashMap,key 是 val 值,value 存放对应的拷贝节点。
因为题目中的条件:每个节点的值都和它的索引相同,且最多为 100 个元素。
所以我们整合(1)(2),使用一个大小为 100 的数组存放拷贝后的元素,同时也可以用来标识是否已经访问过。
深度拷贝
深度拷贝有 2 点:
-
针对节点的拷贝,我们直接创建一个新的 Node(val) 即可。
-
针对邻居节点的拷贝,我们需要 DFS 创建所有邻居节点的拷贝。
java 实现
这里为了让 val 直接访问下标,我们把数组的大小初始化为 101.
// 定义为 101,直接把 val 当做下标,减少一次减法运算。
Node[] copyArray = new Node[101];
public Node cloneGraph(Node node) {
//fast-return
if(node == null) {
return null;
}
// 当前节点
// 节点的位置,就是对应的索引的位置。
int val = node.val;
// 如果已经访问,则直接返回已经复制好的节点
if(copyArray[val] != null) {
return copyArray[val];
}
// 拷贝(不拷贝对应的邻居节点)
Node copy = new Node(val, new ArrayList<>(node.neighbors.size()));
copyArray[val] = copy;
// 复制处理邻居节点
for(Node node1 : node.neighbors) {
copy.neighbors.add(cloneGraph(node1));
}
return copy;
}
效果:
Runtime: 24 ms, faster than 98.98% of Java online submissions for Clone Graph.
Memory Usage: 38.9 MB, less than 87.79% of Java online submissions for Clone Graph.
其他
官方解答中,使用的 HashMap 存放,key 是原始 Node,value 是拷贝的 Node。
这样也可以做到存储,访问标识的作用,而且访问也是 O(1)。
不过我这里没有使用,因为 Node 本身是没有实现 equals() 和 hashcode() 方法的。
不过也有下面的解释:
key是结点类型的指针,那么只有当结点相同时key才会相同,而题目中已经指明了每个结点的val是唯一的,所以val相同一定可以推出结点相同,进而推出Key相同
思路2-BFS 广度优先遍历
既然可以用递归,那么我们接下来看下使用 BFS 怎么实现。
BFS 流程
广度优先搜索类似于树的层次遍历。
从图中的某一顶点出发,遍历每一个顶点时,依次遍历其所有的邻接点,然后再从这些邻接点出发,同样依次访问它们的邻接点。按照此过程,直到图中所有被访问过的顶点的邻接点都被访问到。
最后还需要做的操作就是查看图中是否存在尚未被访问的顶点,若有,则以该顶点为起始点,重复上述遍历的过程。
实现流程
(1)存放当前 node 到 stack 中,拷贝对象放到 copyArray 中。
(2)遍历 stack
弹出元素,遍历对应的邻居节点
如果邻居没有访问过,添加到 stack,拷贝对象设置到 copyArray 中。
将拷贝后的邻居节点,设置到弹出元素对应的 copy 对象的邻居节点
(3)返回 copyArray[node.val]
因为 node.val 放置的就是 node 对应的拷贝信息。
java 实现
Node[] copyArray = new Node[101];
public Node cloneGraph(Node node) {
//fast-return
if(node == null) {
return null;
}
// 当前节点
// 节点的位置,就是对应的索引的位置。
Stack<Node> stack = new Stack<>();
stack.push(node);
// 克隆第一个节点并存储到哈希表中
int val = node.val;
copyArray[val] = new Node(val, new ArrayList<>());
while (!stack.isEmpty()) {
Node pop = stack.pop();
// 处理邻居节点
for(Node neighbor : pop.neighbors) {
// 复制邻居节点
int nVal = neighbor.val;
Node copy = copyArray[nVal];
// 没有访问过
if(copy == null) {
copy = new Node(nVal, new ArrayList<>());
copyArray[nVal] = copy;
stack.push(neighbor);
}
// 更新拷贝的邻居节点
copyArray[pop.val].neighbors.add(copy);
}
}
// 直接获取拷贝后的 node
return copyArray[val];
}
效果:
Runtime: 25 ms, faster than 90.62% of Java online submissions for Clone Graph.
Memory Usage: 39.1 MB, less than 66.44% of Java online submissions for Clone Graph.
回顾,这一题 BFS 其实和 DFS 的整体思路类似,不过 DFS 确实要简洁一点。
借助 stack 实现 BFS 也是必须要熟练掌握的!
应用实战篇
题目
给你一个 m x n 的矩阵 board ,由若干字符 ‘X’ 和 ‘O’ ,找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ’O’ 用 ‘X’ 填充。 示例 1:

输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
示例 2:
输入:board = [["X"]]
输出:[["X"]]
提示:
m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 ‘X’ 或 ‘O’
思路1:DFS
题目最核心的问题就在于判断一个元素 O 是否需要被反转。
(1)任何边界上的 ’O’ 都不会被填充为 ’X’
(2)任何不在边界上,或不与边界上的 ’O’ 相连的 ’O’ 最终都会被填充为 ’X’。
我们可以首先把边界的 O 确认出来,然后以边界的 O 作为起点,进行 DFS,将直接或者间接连接的 O 找到并且进行标记。
最后,我们遍历 board,将标记的 O 进行还原,将没有标记的后,反转为 X。
java 实现
private int m;
private int n;
public void solve(char[][] board) {
m = board.length;
n = board[0].length;
if(m <= 2 || n <= 2) {
return;
}
// 第一行和最后一行
for(int i = 0; i < n; i++) {
dfs(board, 0, i);
dfs(board, m-1, i);
}
// 第一列和最后一列
for(int i = 1; i < m-1; i++) {
dfs(board, i, 0);
dfs(board, i, n-1);
}
// 统一处理
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
if(board[i][j] == '#') {
board[i][j] = 'O';
} else if(board[i][j] == 'O') {
board[i][j] = 'X';
}
}
}
}
private void dfs(char[][] board, int i, int j) {
if(i < 0 || i >= m || j < 0 || j >= n || board[i][j] != 'O') {
return;
}
// 标记
board[i][j] = '#';
dfs(board, i+1, j);
dfs(board, i-1, j);
dfs(board, i, j+1);
dfs(board, i, j-1);
}
效果
Runtime: 1 ms, faster than 99.63% of Java online submissions for Surrounded Regions.
Memory Usage: 41 MB, less than 66.64% of Java online submissions for Surrounded Regions.
复杂度分析
时间复杂度:O(n×m),其中 n 和 m 分别为矩阵的行数和列数。深度优先搜索过程中,每一个点至多只会被标记一次。
空间复杂度:O(n×m),其中 n 和 m 分别为矩阵的行数和列数。主要为深度优先搜索的栈的开销。
dsf 非递归:
非递归的方式,我们需要记录每一次遍历过的位置,我们用 stack 来记录,因为它先进后出的特点。
而位置我们定义一个内部类 Pos 来标记横坐标和纵坐标。
注意的是,在写非递归的时候,我们每次查看 stack 顶,但是并不出 stack,直到这个位置上下左右都搜索不到的时候出 Stack。
class Solution {
public class Pos{
int i;
int j;
Pos(int i, int j) {
this.i = i;
this.j = j;
}
}
public void solve(char[][] board) {
if (board == null || board.length == 0) return;
int m = board.length;
int n = board[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 从边缘第一个是o的开始搜索
boolean isEdge = i == 0 || j == 0 || i == m - 1 || j == n - 1;
if (isEdge && board[i][j] == 'O') {
dfs(board, i, j);
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 'O') {
board[i][j] = 'X';
}
if (board[i][j] == '#') {
board[i][j] = 'O';
}
}
}
}
public void dfs(char[][] board, int i, int j) {
Stack<Pos> stack = new Stack<>();
stack.push(new Pos(i, j));
board[i][j] = '#';
while (!stack.isEmpty()) {
// 取出当前stack 顶, 不弹出.
Pos current = stack.peek();
// 上
if (current.i - 1 >= 0
&& board[current.i - 1][current.j] == 'O') {
stack.push(new Pos(current.i - 1, current.j));
board[current.i - 1][current.j] = '#';
continue;
}
// 下
if (current.i + 1 <= board.length - 1
&& board[current.i + 1][current.j] == 'O') {
stack.push(new Pos(current.i + 1, current.j));
board[current.i + 1][current.j] = '#';
continue;
}
// 左
if (current.j - 1 >= 0
&& board[current.i][current.j - 1] == 'O') {
stack.push(new Pos(current.i, current.j - 1));
board[current.i][current.j - 1] = '#';
continue;
}
// 右
if (current.j + 1 <= board[0].length - 1
&& board[current.i][current.j + 1] == 'O') {
stack.push(new Pos(current.i, current.j + 1));
board[current.i][current.j + 1] = '#';
continue;
}
// 如果上下左右都搜索不到,本次搜索结束,弹出stack
stack.pop();
}
}
}
bfs 非递归:
dfs 非递归的时候我们用 stack 来记录状态,而 bfs 非递归,我们则用队列来记录状态。
和 dfs 不同的是,dfs 中搜索上下左右,只要搜索到一个满足条件,我们就顺着该方向继续搜索,所以你可以看到 dfs 代码中,只要满足条件,就入 Stack,然后 continue 本次搜索,进行下一次搜索,直到搜索到没有满足条件的时候出 stack。
而 dfs 中,我们要把上下左右满足条件的都入队,所以搜索的时候就不能 continue。
大家可以对比下两者的代码,体会 bfs 和 dfs 的差异。
class Solution {
public class Pos{
int i;
int j;
Pos(int i, int j) {
this.i = i;
this.j = j;
}
}
public void solve(char[][] board) {
if (board == null || board.length == 0) return;
int m = board.length;
int n = board[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 从边缘第一个是o的开始搜索
boolean isEdge = i == 0 || j == 0 || i == m - 1 || j == n - 1;
if (isEdge && board[i][j] == 'O') {
bfs(board, i, j);
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 'O') {
board[i][j] = 'X';
}
if (board[i][j] == '#') {
board[i][j] = 'O';
}
}
}
}
public void bfs(char[][] board, int i, int j) {
Queue<Pos> queue = new LinkedList<>();
queue.add(new Pos(i, j));
board[i][j] = '#';
while (!queue.isEmpty()) {
Pos current = queue.poll();
// 上
if (current.i - 1 >= 0
&& board[current.i - 1][current.j] == 'O') {
queue.add(new Pos(current.i - 1, current.j));
board[current.i - 1][current.j] = '#';
// 没有continue.
}
// 下
if (current.i + 1 <= board.length - 1
&& board[current.i + 1][current.j] == 'O') {
queue.add(new Pos(current.i + 1, current.j));
board[current.i + 1][current.j] = '#';
}
// 左
if (current.j - 1 >= 0
&& board[current.i][current.j - 1] == 'O') {
queue.add(new Pos(current.i, current.j - 1));
board[current.i][current.j - 1] = '#';
}
// 右
if (current.j + 1 <= board[0].length - 1
&& board[current.i][current.j + 1] == 'O') {
queue.add(new Pos(current.i, current.j + 1));
board[current.i][current.j + 1] = '#';
}
}
}
}
并查集:
并查集这种数据结构好像大家不太常用,实际上很有用,我在实际的 production code 中用过并查集。
并查集常用来解决连通性的问题,即将一个图中连通的部分划分出来。当我们判断图中两个点之间是否存在路径时,就可以根据判断他们是否在一个连通区域。
而这道题我们其实求解的就是和边界的 OO 在一个连通区域的的问题。
并查集的思想就是,同一个连通区域内的所有点的根节点是同一个。将每个点映射成一个数字。先假设每个点的根节点就是他们自己,然后我们以此输入连通的点对,然后将其中一个点的根节点赋成另一个节点的根节点,这样这两个点所在连通区域又相互连通了。 并查集的主要操作有:
find(int m):这是并查集的基本操作,查找 mm 的根节点。
isConnected(int m,int n):判断 m,nm,n 两个点是否在一个连通区域。
union(int m,int n):合并 m,nm,n 两个点所在的连通区域。
class UnionFind {
int[] parents;
public UnionFind(int totalNodes) {
parents = new int[totalNodes];
for (int i = 0; i < totalNodes; i++) {
parents[i] = i;
}
}
// 合并连通区域是通过find来操作的, 即看这两个节点是不是在一个连通区域内.
void union(int node1, int node2) {
int root1 = find(node1);
int root2 = find(node2);
if (root1 != root2) {
parents[root2] = root1;
}
}
int find(int node) {
while (parents[node] != node) {
// 当前节点的父节点 指向父节点的父节点.
// 保证一个连通区域最终的parents只有一个.
parents[node] = parents[parents[node]];
node = parents[node];
}
return node;
}
boolean isConnected(int node1, int node2) {
return find(node1) == find(node2);
}
}
我们的思路是把所有边界上的 OO 看做一个连通区域。遇到 OO 就执行并查集合并操作,这样所有的 OO 就会被分成两类
-
和边界上的 OO 在一个连通区域内的。这些 OO 我们保留。
-
不和边界上的 OO 在一个连通区域内的。这些 OO 就是被包围的,替换。
由于并查集我们一般用一维数组来记录,方便查找 parants,所以我们将二维坐标用 node 函数转化为一维坐标。
public void solve(char[][] board) {
if (board == null || board.length == 0)
return;
int rows = board.length;
int cols = board[0].length;
// 用一个虚拟节点, 边界上的O 的父节点都是这个虚拟节点
UnionFind uf = new UnionFind(rows * cols + 1);
int dummyNode = rows * cols;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
if (board[i][j] == 'O') {
// 遇到O进行并查集操作合并
if (i == 0 || i == rows - 1 || j == 0 || j == cols - 1) {
// 边界上的O,把它和dummyNode 合并成一个连通区域.
uf.union(node(i, j), dummyNode);
} else {
// 和上下左右合并成一个连通区域.
if (i > 0 && board[i - 1][j] == 'O')
uf.union(node(i, j), node(i - 1, j));
if (i < rows - 1 && board[i + 1][j] == 'O')
uf.union(node(i, j), node(i + 1, j));
if (j > 0 && board[i][j - 1] == 'O')
uf.union(node(i, j), node(i, j - 1));
if (j < cols - 1 && board[i][j + 1] == 'O')
uf.union(node(i, j), node(i, j + 1));
}
}
}
}
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
if (uf.isConnected(node(i, j), dummyNode)) {
// 和dummyNode 在一个连通区域的,那么就是O;
board[i][j] = 'O';
} else {
board[i][j] = 'X';
}
}
}
}
int node(int i, int j) {
return i * cols + j;
}
}
NEXT
参考资料
https://leetcode-cn.com/problems/surrounded-regions/solution/bfsdi-gui-dfsfei-di-gui-dfsbing-cha-ji-by-ac_pipe/
https://www.guyuehome.com/11046
https://lucifer.ren/leetcode/thinkings/DFS.html
https://developer.aliyun.com/article/49140
https://blog.csdn.net/weixin_42638946/article/details/114993465
https://blog.csdn.net/qq_40310148/article/details/106786652
