上一讲主要内容回顾(Last time):
-
基于转换的标注器(Transformation-based tagger)
-
基于隐马尔科夫模型的标注器(HMM-based tagger)
遗留的内容(Leftovers):
a) 词性分布(POS distribution)
i. 在Brown语料库中按歧义程度排列的词型数目(The number of word types in Brown corpus by degree of ambiguity):
无歧义(Unambiguous)只有1个标记: 35,340
歧义(Ambiguous)
有2-7个标记: 4,100 2个标记:3,764 3个标记:264 4个标记:61 5个标记:12 6个标记:2 7个标记:1
b) 无监督的TBL(Unsupervised TBL)
i. 初始化(Initialization):允许的词性列表(a list of allowable part of speech tags)
ii. 转换(Transformations): 在上下文C中将一个单词的标记从χ变为Y (Change the tag of a word from χ to Y in context C, where γ ∈ χ).
例子(Example): “From NN VBP to VBP if previous tag is NNS”
iii. 评分标准(Scoring criterion):
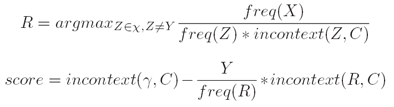
这一讲主要内容(Today):
-
最大熵模型(Maximum entropy models)
-
与对数线性模型的联系(Connection to log-linear models)
-
优化方法(Optimization methods)
一般问题描述(The General Problem):
a) 给定输入域χ(We have some input domain χ);
b) 给定标记集γ(We have some label set γ);
c) 目标(Goal):对于任何x ∈ χ 及 y ∈γ学习一个条件概率 P(y|x) (learn a conditional probability P(y |
x)for any x ∈ χ and y ∈ γ )。 |
一、 词性标注(POS tagging):
a) 例子:
Our/PRP$ enemies/NNS are/VBP innovative/JJ and/CC resourceful/JJ ,/, and/CC so/RB are/VB we/PRP ?/?.
i. 输入域(Input domain):χ是可能的“历史”(χ is the set of possible histories);
ii. 标记集(Label set):γ是所有可能的标注标记(γ is the set of all possible tags);
| iii. 目标(Goal):学习一个条件概率P(tag | history)(learn a conditional probability P(tag | history))。 |
b) 表现形式(Representation):
i. “历史”是一个4元组(t1,t2,w[1:n],i) (History is a 4-tuples (t1,t2,w[1:n],i);
ii. t1,t2是前两个标记(t1,t2 are the previous two tags)
iii. w[1:n]是输入句子中的n个单词(w[1:n]are the n words in the input sentence)
iv. i 是将要被标注的单词的位置索引(i is the index of the word being tagged)
χ是所有可能的“历史”集合(χis the set of all possible histories)
c) 特征向量表示(Feature Vector Representation)
i. 一个特征就是一个函数f(A feature is a function f ):
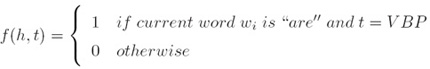
ii. 我们有m个特征fk,k = 1…m(We have m features fk for k =1…m)
d) 词性表示(POS Representation)
i. 对于所有的单纯/标记对的单词/标记特征,(Word/tag features for all word/tag pairs):
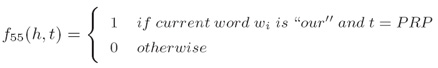
ii. 对于所有特定长度的前缀/后缀的拼写特征(Spelling features for all prefixes/suffixes of certain length)
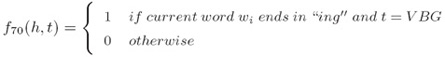
iii. 上下文特征(Contextual features):
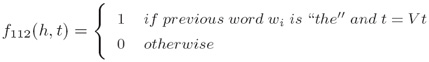
iv. 对于一个给定的“历史”x ∈ X ,每一个γ中的标记都被映射到一个不同的特征向量(For a given history x ∈ X, each label in γ is mapped to a different feature vector):
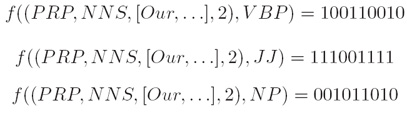
v. 目标(Goal):
学习一个条件概率 P(tag|history)(learn a conditional probability P(tag|history)
二、 最大熵(Maximum Entropy):
a) 例子(Motivating Example):
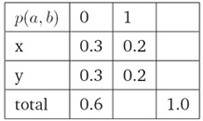
i. 给定约束条件:p(x, 0)+p(y, 0)=0.6,a ∈{x, y}且b ∈0, 1,估计概率分布p(a, b)(Estimate probability distribution p(a, b), given the constraint: p(x, 0) + p(y, 0) =0.6, where a ∈{x, y}and b ∈0, 1)):
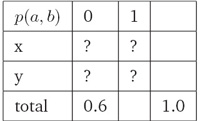
ii. 满足约束条件的一种分布(One Way To Satisfy Constraints):
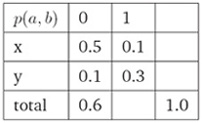
iii. 满足约束条件的另一种分布(Another Way To Satisfy Constraints):
b) 最大熵模型(Maximum Entropy Modeling)
i. 给定一个训练样本集,我们希望寻找一个分布符合如下两个条件(Given a set of training examples, we wish to find a distribution which):
-
满足已知的约束条件(satisfies the input constraints)
-
最大化其不确定性(maximizes the uncertainty)
ii. 补充:
最大熵原理是在1957 年由E.T.Jaynes 提出的,其主要思想是,
在只掌握关于未知分布的部分知识时,应该选取符合这些知识但熵值最大的概率分布。
因为在这种情况下,符合已知知识的概率分布可能不止一个。
我们知道,熵定义的实际上是一个随机变量的不确定性,熵最大的时侯,说明随机变量最不确定,换句话说,也就是随机变量最随机,对其行为做准确预测最困难。
从这个意义上讲,那么最大熵原理的实质就是,在已知部分知识的前提下,关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断,这是我们可以作出的唯一不偏不倚的选择,任何其它的选择都意味着我们增加了其它的约束和假设,这些约束和假设根据我们掌握的信息无法做出。
(这一段转自北大常宝宝老师的《自然语言处理的最大熵模型》)
b) 最大熵模型(Maximum Entropy Modeling)
iii. 约束条件(Constraint):
每个特征的观察样本期望值与特征模型期望值相一致(observed expectation of each feature has to be the same as the model’s expectation of the feature):
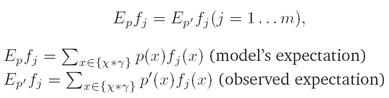
iv. 最大熵原理(Principle of Maximum Entropy):
将已知事实作为制约条件,求得可使熵最大化的概率分布作为正确的概率分布:
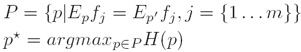
v. 补充:
自然语言处理中很多问题都可以归结为统计分类问题,很多机器学习方法在这里都能找到应用,在自然语言处理中,统计分类表现在要估计类a 和某上下文b 共现的概率P(a,b) ,不同的问题,类a 和上下文b 的内容和含义也不相同。
在词性标注中是类的含义是词性标注集中的词类标记,而上下文指的是当前被处理的词前面一个词及词类,后面一个词及词类或前后若干个词和词类。
通常上下文有时是词,有时是词类标记,有时是历史决策等等。
大规模语料库中通常包含a 和b 的共现信息,但b 在语料库中的出现常常是稀疏的,要对所有可能的(a,b)计算出可靠的P(a,b) ,语料库规模往往总是不够的。
问题是要发现一个方法,利用这个方法在数据稀疏的条件下可靠的估计P(a,b) 。不同的方法可能采用不同的估计方法。
最大熵模型的优点是:在建模时,试验者只需要集中精力选择特征,而不需要花费精力考虑如何使用这些特征。而且可以很灵活地选择特征,使用各种不同类型的特征,特征容易更换。
利用最大熵建模,一般也不需要做在其它方法建模中常常使用的独立性假设,参数平滑可以通过特征选择的方式加以考虑,无需专门使用常规平滑算法单独考虑,当然也不排除使用经典平滑算法进行平滑。
每个特征对概率分布的贡献则由参数α决定,该参数可以通过一定的算法迭代训练得到。 (注:以上两段转自北大常宝宝老师的《自然语言处理的最大熵模型》)
最大熵模型详述
a) 概要(Outline)
i. 我们将首先证明(We will first show that)满足上述条件的概率分布p*具有如下的形式:
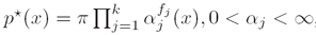
其中pi是一个归一化常数,α是模型参数(where pi is a normalization constant and the α’s are the model parameters)
ii. 然后我们将考虑搜寻α的参数估计过程(Then, we will consider an estimation procedure for finding the α’s)
b) 数学符号表示(Notations)
i. χ是可能的“历史”集(χis the set of possible histories)
ii. γ是所有可能的标记集(γ is the set of all possible tags)
iii. S是事件训练样本集(S finite training sample of events)
iv. p’(x)是S中x的观察概率(p’(x)observed probability of x in S)
v. p(x)是x的模型概率(p(x) the model’s probability of x)
vi. 其它符号公式定义如下:
c) 相对熵(Kullback-Liebler距离)(Relative Entropy (Kullback-Liebler Distance))
i. 定义(Definition):
两个概率分布p和q的相对熵D由下式给出(The relative entropy D between two probability distributions p and q is given by)
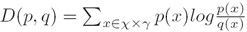
ii. 引理1(Lemma 1):
对于任意两个概率分布p和q,D(p, q)≥0 且 D(p, q)=0 当且仅当p=q(For any two probability distributions p and q, D(p, q)≥ 0, and D(p, q)=0 if and only if p =q)
iii. 引理2(毕达哥拉斯性质)(Lemma 2 (Pythagorean Property)):
若p∈P,q∈Q,p*∈P∩Q,则D(p, q) = D(p, p*) + D(p*, q) (If p ∈P and q ∈ Q, and p*∈P∩Q, then D(p, q) = D(p, p*) + D(p*, q))
注:证明请参看MIT NLP 的lec5.pdf英文讲稿;
d) 最大熵解(The Maximum Entropy Solution)
i. 定理1(Theorem 1):
若p*∈P∩Q,则p* = argmax_{p in P}H(p) ,且p*唯一(If p∗∈P ∩Q then p* = argmax_{p in P}H(p). Furthermore, p* is unique)
注:证明请参看min nlp原讲稿,主要运用引理1和引理2得出。
e) 最大似然解(The Maximum Likelihood Solution)
i. 定理2(Theorem 2):
若p*∈P∩Q,则p* = argmax_{q in Q}L(q) ,且p*唯一(If p∗∈P ∩Q then p* = argmax_{q in Q}L(q). Furthermore, p* is unique)
注:证明请参看min nlp原讲稿,主要运用引理1和引理2得出。
f) 对偶定理(Duality Theorem)
i. 存在一个唯一分布p(There is a unique distribution p)
-
p*∈ P ∩ Q
-
p* = argmax_{p in P}H(p) (最大熵解(Max-ent solution))
-
p* = argmax_{q in Q}L(q) (最大似然解(Max-likelihood solution))
ii. 结论(Implications):
-
最大熵解可以写成对数线性形式(The maximum entropy solution can be written in log-linear form)
-
求出最大似然解同样给出了最大熵解(Finding the maximum-likelihood solution also gives the maximum entropy solution)
GIS算法(Generative Iterative Scaling)
i. 背景:
最原始的最大熵模型的训练方法是一种称为通用迭代算法GIS (generalized iterative scaling) 的迭代算法。
GIS 的原理并不复杂,大致可以概括为以下几个步骤:
-
假定第零次迭代的初始模型为等概率的均匀分布。
-
用第 N 次迭代的模型来估算每种信息特征在训练数据中的分布,如果超过了实际的,就把相应的模型参数变小;否则,将它们变大。
-
重复步骤 2 直到收敛。
GIS 最早是由 Darroch 和 Ratcliff 在七十年代提出的。
但是,这两人没有能对这种算法的物理含义进行很好地解释。
后来是由数学家希萨(Csiszar) 解释清楚的,因此,人们在谈到这个算法时,总是同时引用 Darroch 和Ratcliff 以及希萨的两篇论文。
GIS 算法每次迭代的时间都很长,需要迭代很多次才能收敛,而且不太稳定,即使在 64 位计算机上都会出现溢出。
因此,在实际应用中很少有人真正使用 GIS。大家只是通过它来了解最大熵模型的算法。
IIS 优化
八十年代,很有天才的孪生兄弟的达拉皮垂(Della Pietra)在 IBM 对 GIS 算法进行了两方面的改进,提出了改进迭代算法 IIS(improved iterative scaling)。
这使得最大熵模型的训练时间缩短了一到两个数量级。
这样最大熵模型才有可能变得实用。
即使如此,在当时也只有 IBM 有条件是用最大熵模型。(以上摘自Google吴军《数学之美系列16》)
ii. 目标(Goal):
寻找遵循如下约束条件的此种形式pi prod{j=1}{k}【alpha_j}^{f_j}(x)}的分布(Find distribution of the form pi prod{j=1}{k}【alpha_j}^{f_j}(x)}that obeys the following constraints):E_p f_j = E_{p prime}{f_j}
iii. GIS 约束条件(GIS constraints):
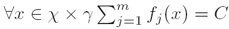
其中C是一个常数(where C is a constant (add correctional feature))
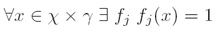
iv. 定理(Theorem):
下面的过程将收敛到p∈P∩Q(The following procedure will converge to p∈P∩Q):
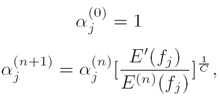
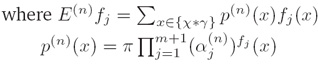
v. 计算量(Computation)
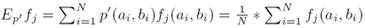
其中S={(a1,b1),…,(aN,bN)}是训练样本(where S is a training sample)
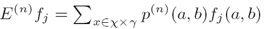
因为有太多可能的(a,b),为了减少计算量,因而采用下面的公式近似计算:
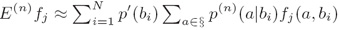
时间复杂度(Running time):O(NPA)
其中N训练集规模,P是预期数,A是对于给定事件(a,b)活跃特征的平均数(where N is the training set size, P is the number of predictions, and A is the average number of features that are active for a given event (a,b))
最大熵分类器(ME classifiers)
a) 可以处理很多特征(Can handle lots of features)
b) 存在数据稀疏问题(Sparsity is an issue)
i. 应用平滑算法和特征选择方法解决(apply smoothing and feature selection)
c) 特征交互(Feature interaction)?
i. 最大熵分类器并没有假设特征是独立的(ME classifiers do not assume feature independence)
ii. 然而,它们也没有明显的模型特征交互(However, they do not explicitly model feature interaction)
总结(Summary)
a) 条件概率建模与对数线性模型(Modeling conditional probabilities with log-linear models)
b) 对数线性模型的最大熵性质(Maximum-entropy properties of log-linear models)
c) 通过迭代缩放进行优化(Optimization via iterative scaling)
一些实现的最大熵工具(Some implementations):
http://nlp.stanford.edu/downloads/classifier.shtml
http://maxent.sourceforge.net
拓展学习
TODO
MIT 系列的深入学习+实战
http://www.52nlp.cn/mit-open-course-natural-language-processing-introduce
