数组
大家好,我是老马。
今天我们一起来学习一下数组这种数据结构。
主要知识
数组需要拆分下面几个部分:
-
理论介绍
-
源码分析
-
数据结构实现?
-
题目练习(按照算法思想分类)
-
梳理对应的 sdk 包
-
应用实战
因为这个是 leetcode 系列,所以重点是 4、5(对4再一次总结)。
为了照顾没有基础的小伙伴,会简单介绍一下1的基础理论。
简单介绍1,重点为4。其他不是本系列的重点。
LC133 克隆图 clone-graph
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
class Node {
public int val;
public List
测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
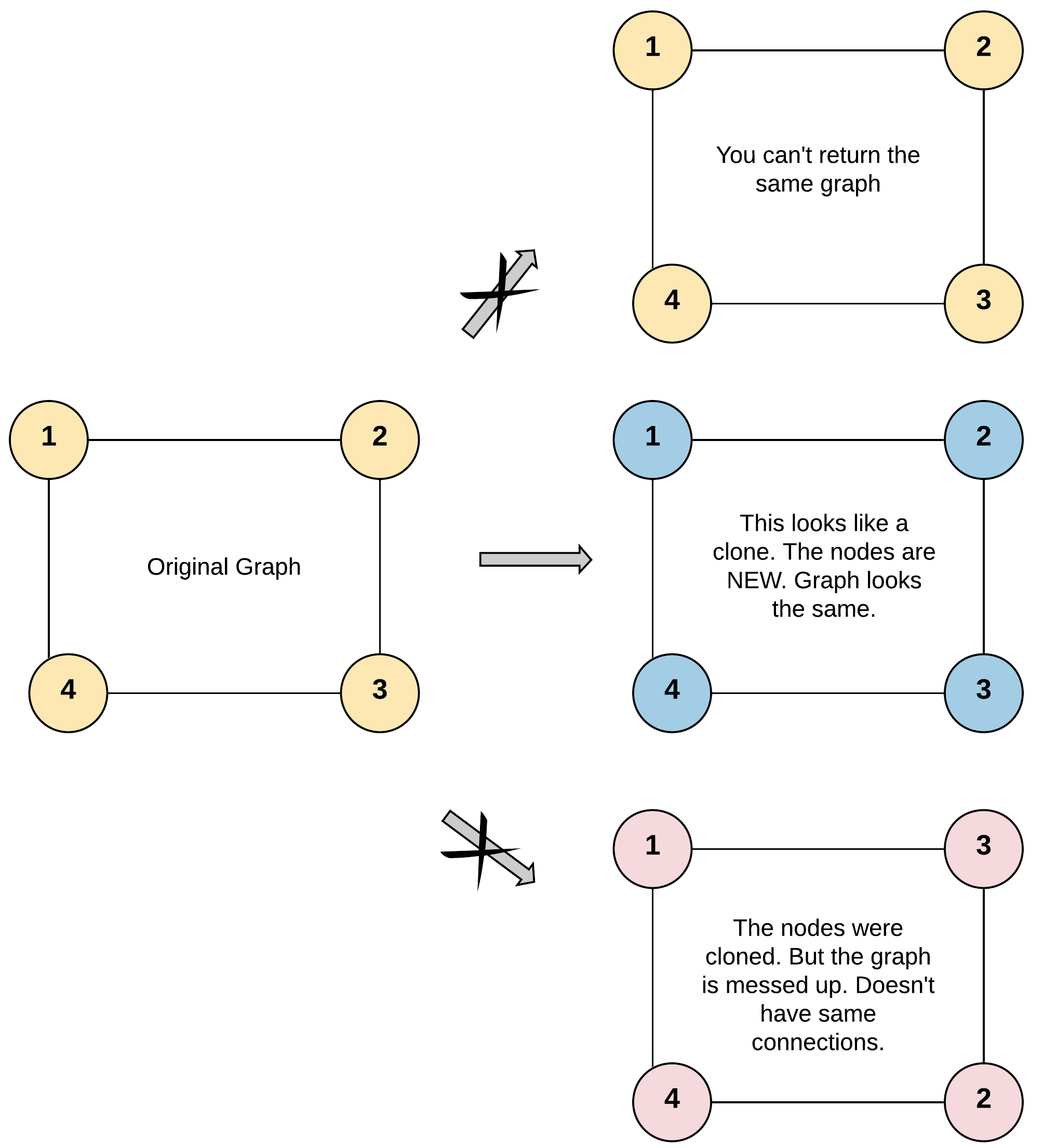
输入:adjList = [[2,4],[1,3],[2,4],[1,3]] 输出:[[2,4],[1,3],[2,4],[1,3]] 解释: 图中有 4 个节点。 节点 1 的值是 1,它有两个邻居:节点 2 和 4 。 节点 2 的值是 2,它有两个邻居:节点 1 和 3 。 节点 3 的值是 3,它有两个邻居:节点 2 和 4 。 节点 4 的值是 4,它有两个邻居:节点 1 和 3 。
示例 2:
2
输入:adjList = [[]] 输出:[[]] 解释:输入包含一个空列表。该图仅仅只有一个值为 1 的节点,它没有任何邻居。
示例 3:
输入:adjList = [] 输出:[] 解释:这个图是空的,它不含任何节点。
提示:
这张图中的节点数在 [0, 100] 之间。 1 <= Node.val <= 100 每个节点值 Node.val 都是唯一的, 图中没有重复的边,也没有自环。 图是连通图,你可以从给定节点访问到所有节点。
v1-基本思路 DFS
思路
递归
我们利用 Map 存出一个 node 是否访问过。
1) 终止条件:
if(node == null) {
return null;
}
if(map.containsKey(node)) {
return map.get(node);
}
2) 业务处理
复制当前节点信息
同时拷贝 dfs 邻居节点
实现
public Node cloneGraph(Node node) {
Map<Node, Node> visited = new HashMap<>();
return dfs(node, visited);
}
private Node dfs(Node node, Map<Node, Node> visited) {
if(node == null) {
return null;
}
if(visited.containsKey(node)) {
return visited.get(node);
}
Node root = new Node();
root.val = node.val;
visited.put(node, root); // 记得先放入 visited 防止环
// 递归处理邻居节点
List<Node> neighbors = new ArrayList<>();
for(Node nei : node.neighbors) {
neighbors.add(dfs(nei, visited));
}
root.neighbors = neighbors;
return root;
}
效果
25ms 击败 84.91%
复杂度
v2-BFS
思路
类似的,我们可以使用 queue 来实现 BFS
1)利用 map 来缓存已经创建的节点
2)首先 cache root 节点
邻居节点,不存在才创建处理。并且放入 cache 中
实现
public Node cloneGraph(Node node) {
if (node == null) return null; // 防止空指针
Map<Node, Node> visited = new HashMap<>();
Queue<Node> queue = new LinkedList<>();
queue.offer(node);
Node copy = new Node();
copy.val = node.val;
visited.put(node, copy);
while(!queue.isEmpty()) {
Node tempNode = queue.poll();
Node cloneNode = visited.get(tempNode);
// linju
List<Node> neiList = new ArrayList<>();
for(Node nei : tempNode.neighbors) {
if(!visited.containsKey(nei)) {
Node copyNei = new Node();
copyNei.val = nei.val;
visited.put(nei, copyNei);
// 重新入栈
queue.offer(nei);
}
neiList.add(visited.get(nei));
}
cloneNode.neighbors = neiList;
}
return copy;
}
效果
29 ms 击败 12.31%
v3-Stack 模拟 DFS
思路
类似的,我们也可以用 stack 来模拟实现。
实现
public Node cloneGraph(Node node) {
if (node == null) return null; // 防止空指针
Map<Node, Node> visited = new HashMap<>();
Stack<Node> stack = new Stack<>();
stack.push(node);
Node copy = new Node();
copy.val = node.val;
visited.put(node, copy);
while(!stack.isEmpty()) {
Node tempNode = stack.pop();
Node cloneNode = visited.get(tempNode);
// linju
List<Node> neiList = new ArrayList<>();
for(Node nei : tempNode.neighbors) {
if(!visited.containsKey(nei)) {
Node copyNei = new Node();
copyNei.val = nei.val;
visited.put(nei, copyNei);
// 重新入栈
stack.push(nei);
}
neiList.add(visited.get(nei));
}
cloneNode.neighbors = neiList;
}
return copy;
}
效果
34ms 击败 6.57%
