leetcode 算法篇专题之链表 Linkedlist 02-LC25. K 个一组翻转链表 reverse-nodes-in-k-group

数组

大家好，我是老马。

今天我们一起来学习一下数组这种数据结构。

主要知识

数组需要拆分下面几个部分：

1. 理论介绍

2. 源码分析

3. 数据结构实现？

4. 题目练习（按照算法思想分类）

5. 梳理对应的 sdk 包

6. 应用实战

因为这个是 leetcode 系列，所以重点是 4、5(对4再一次总结)。

为了照顾没有基础的小伙伴，会简单介绍一下1的基础理论。

简单介绍1，重点为4。其他不是本系列的重点。

数据结构篇

https://leetcode.cn/studyplan/top-100-liked/

历史回顾

【leetcode】013-25.K 个一组翻转链表 Reverse Nodes in k-Group + 24. 两两交换链表中的节点 swap nodes in pairs

leetcode 算法篇专题之链表 Linkedlist 02-LC206. 反转链表 reverse-linked-list

LC 24. 两两交换链表中的节点

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

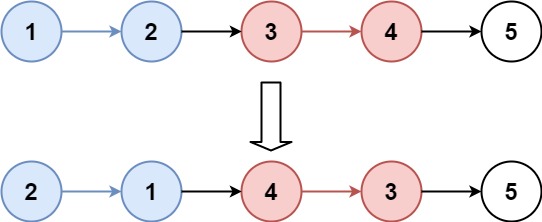
输入：head = [1,2,3,4,5], k = 2 输出：[2,1,4,3,5]

示例 2：

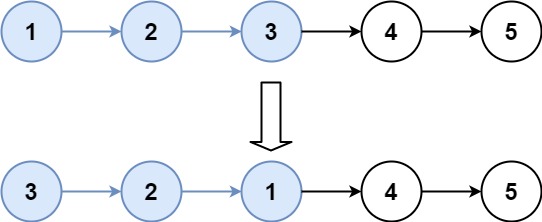
输入：head = [1,2,3,4,5], k = 3 输出：[3,2,1,4,5]

提示： 链表中的节点数目为 n 1 <= k <= n <= 5000 0 <= Node.val <= 1000

进阶：你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

v0-借助额外空间

思路

类似于 T24，我们把交换的部分拓展一下即可。

我们只是把 swap 2个一组反转，改为了从 [i,i+k-1] k 个一组反转。

反转通过双指针 swap 实现。

实现

private List<ListNode> getListNodes(ListNode head) {
        List<ListNode> list = new ArrayList<>();
        while (head != null) {
            list.add(head);
            head = head.next;
        }
        return list;
    }

    public static  void reverse(List<ListNode> list, int i, int j) {
        if (i < 0 || j >= list.size() || i >= j) {
            return; // 索引无效或不需要反转
        }
        while (i < j) {
            ListNode temp = list.get(i);
            list.set(i, list.get(j));
            list.set(j, temp);
            i++;
            j--;
        }
    }

    public ListNode reverseKGroup(ListNode head, int k) {
        if(head == null) {
            return null;
        }

        // 所有节点
        List<ListNode> listNodes = getListNodes(head);

        // 按照组交换
        for(int i = 0; i < listNodes.size(); i += k) {
            // 结束循环
            if(i+k-1 > listNodes.size()-1) {
                break;
            }

            reverse(listNodes, i, i+k-1);
        }

        // 设置->
        for(int i = 0; i < listNodes.size()-1; i++) {
            listNodes.get(i).next = listNodes.get(i+1);
        }
        // 最后一个设置为 null
        listNodes.get(listNodes.size()-1).next = null;

        // 返回
        return listNodes.get(0);
    }

效果

3ms 击败 2.88%

反思

优点：逻辑直观，几乎不用考虑指针操作。

缺点：需要 O(n) 额外空间，不是原地操作。性能不佳。

v1-快慢指针

T25 回顾

我们回顾一下 T24 的交换实现

 public static ListNode swapPairs(ListNode head) {
        ListNode dummy = new ListNode(0, head);
        ListNode prev = dummy;

        // 修改点1：这里找下一个节点，要改为找第 k 个节点
        while (prev.next != null && prev.next.next != null) {
            ListNode first = prev.next;
            ListNode second = first.next;

            // 执行交换
            // 修改点2：以前是2个一组交换，要改为 k 个一组交换
            first.next = second.next;
            second.next = first;
            prev.next = second;

            // 移动 prev 到已处理块的尾（first）
            // 修改点3：整体的链表接的逻辑要调整下
            prev = first;
        }

        return dummy.next;
}

思路

1）获取第 kth 的节点，从指定 node 开始，循环 k 次获取 k-th 的节点 kthNode

2）初始化

// 当前组的开始，是 pre.next
ListNode curGroupStart = prev.next;
ListNode nextGroupStart = kthNode.next;

3) 反转

双指针反转 [curGroupStart,...,kthNode]，类似 v1 的 reverse

4) 衔接块

因为 pre->[curGroupStart,...,kthNode]->nextGroupStart

已经反转了，形成了

pre->[kthNode,...,curGroupStart]->nextGroupStart

所以：

// 上一次的结尾->当前组本来的最后一个元素
pre.next = kthNode;
// 当前组本来的开始-》以前的下一个组的开始
curGroupStart.next = nextGroupStart;

5) 更新

最后，更新一个 pre，移动到当前交换组的结尾

pre = curGroupStart;

反转

这里我们可以参考下 LC206-链表反转

实现如下：

    // 反转从 start 到 end 的链表（包含两端）
    private void reverse(ListNode start, ListNode end) {
        ListNode pre = end.next;
        ListNode cur = start;

        // 和 LC206 的区别，不是整体反转。而是到 end.next 就结束了
        while (pre != end) {
            //1->2->3->...
            // 临时节点，避免 cur-> 指向反转时，引用丢失
            ListNode tmp = cur.next;

            // 指向反转
            cur.next = pre;

            // 更新节点
            pre = cur;
            // cur 指向本来 cur->next，方便做剩余的反转
            cur = tmp;
        }
    }

整体实现

    public ListNode reverseKGroup(ListNode head, int k) {
        if(head == null) {
            return null;
        }

        ListNode dummy = new ListNode(0, head);
        ListNode pre = dummy;

        while (true) {
            //1. 找到第 k 个元素，不够 k 个直接结束
            ListNode kthNode = findKthNode(pre, k);
            if(kthNode == null) {
                break;
            }

            //2. 当前的开始+下一组的开头
            ListNode curGroupStart = pre.next;
            ListNode nextGroupStart = kthNode.next;

            //3. 翻转
            reverse(curGroupStart, kthNode);

            //4. 衔接
            pre.next = kthNode;
            curGroupStart.next = nextGroupStart;

            //5. 更新 pre
            pre = curGroupStart;
        }

        return dummy.next;
    }

    // 反转从 start 到 end 的链表（包含两端）
    private void reverse(ListNode start, ListNode end) {
        ListNode pre = end.next;
        ListNode cur = start;

        // 和 LC206 的区别，不是整体反转。而是到 end.next 就结束了
        while (pre != end) {
            //1->2->3->...
            // 临时节点，避免 cur-> 指向反转时，引用丢失
            ListNode tmp = cur.next;

            // 指向反转
            cur.next = pre;

            // 更新节点
            pre = cur;
            // cur 指向本来 cur->next，方便做剩余的反转
            cur = tmp;
        }
    }

    private ListNode findKthNode(ListNode node, int k) {
        while (k > 0 && node != null) {
            node = node.next;

            k--;
        }
        return node;
    }

效果

0ms 击败 100.00%

反思

和 T24 类似。

只不过调整了两个部分：

1）首先找 kth 节点

2）swap 改为了范围的 reverse

v2-递归

思路

递归的本质是把大问题拆成“小的同类问题”。

思路是：

类似的，我们给一下递归的解法，整体逻辑类似。

注意：

1）getKthNode 调整了下，因为以前是从 pre 节点 开始找的，这次直接从 curNode 开始，应该少一次。

实现

(n1->n2)->(n3->n4)->(….)

交换后

(n2->n1)->(n4->n3)->(….)

public ListNode reverseKGroup(ListNode head, int k) {
        // 1. 找到第 k 个节点
        ListNode kth = getKthNode(head, k);
        if (kth == null) {
            // 不足 k 个，直接返回当前 head
            return head;
        }

        // 2. 记录下一组的头节点
        ListNode nextGroupHead = kth.next;

        // 3. 反转当前区间 [head, kth]
        reverse(head, kth);

        // 4. head 现在是反转后的尾节点，递归反转后续节点
        head.next = reverseKGroup(nextGroupHead, k);

        // 5. kth 是反转后当前段的新头，返回它
        return kth;
    }

    // 反转链表从 start 到 end，包含两端节点
    private void reverse(ListNode start, ListNode end) {
        ListNode prev = end.next;
        ListNode curr = start;
        while (prev != end) {
            ListNode nextTemp = curr.next;
            curr.next = prev;
            prev = curr;
            curr = nextTemp;
        }
    }

    // 获取从 node 开始第 k 个节点（包括 node 自身）
    private ListNode getKthNode(ListNode node, int k) {
        while (node != null && k > 1) {
            node = node.next;
            k--;
        }
        return node;
    }

效果

0ms 击败 100.00%

反思

递归看起来更加整洁，但是逻辑是一样的。

• 数组
  • 主要知识
• 数据结构篇
  • 历史回顾
• LC 24. 两两交换链表中的节点
• v0-借助额外空间
  • 思路
  • 实现
  • 效果
  • 反思
• v1-快慢指针
  • T25 回顾
  • 思路
  • 反转
  • 整体实现
  • 效果
  • 反思
• v2-递归
  • 思路
  • 实现
  • 效果
  • 反思