在力扣中，“图”通常指由 顶点（Nodes / Vertices） 和 边（Edges） 组成的数据结构。图可以是：
A -> B 表示只能从 A 到 B。A - B 表示 A 可以到 B，B 也可以到 A。完全可以先确认一点：在图中，理论上只要能用 DFS 遍历的图，也可以用 BFS 遍历，因为两者都是遍历整个连通分量的算法。
它们的根本区别不在“能否遍历”，而在遍历顺序、应用场景和性能差异。
下面详细分析：
| 特性 | DFS | BFS |
|---|---|---|
| 遍历顺序 | 深度优先，尽可能沿一条路径走到底再回溯 | 广度优先，按层（距离起点的步数）访问 |
| 数据结构 | 栈 / 递归调用栈 | 队列 |
| 访问顺序 | 先访问子节点最深的路径 | 先访问距离起点最近的节点 |
| 适用场景 | 搜索路径、连通分量、拓扑排序、回溯 | 最短路径（无权图）、层序问题、分层处理 |
| 性能 | 空间复杂度受递归深度影响（最坏 O(V)） | 空间复杂度受队列影响（最坏 O(V)） |
在图论中，**连通性（Connectivity）**描述图中节点之间可达的关系：
节点可达（Reachability）：如果存在一条从节点 A 到节点 B 的路径，则称 A 可达 B。
连通图（Connected Graph）：
无向图：如果任意两个节点之间都有路径，称图是连通的。
有向图：
有 n 个房间，房间按从 0 到 n - 1 编号。最初，除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而，你不能在没有获得钥匙的时候进入锁住的房间。
当你进入一个房间，你可能会在里面找到一套 不同的钥匙，每把钥匙上都有对应的房间号，即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。
给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true，否则返回 false。
示例 1：
输入：rooms = [[1],[2],[3],[]]
输出：true
解释：
我们从 0 号房间开始，拿到钥匙 1。
之后我们去 1 号房间，拿到钥匙 2。
然后我们去 2 号房间，拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间，我们返回 true。
有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
示例 1：
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2
示例 2：
n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。
路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。
今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。
请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。
题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。
给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。
给你一个 m x n 的迷宫矩阵 maze （下标从 0 开始），矩阵中有空格子（用 '.' 表示）和墙（用 '+' 表示）。同时给你迷宫的入口 entrance ，用 entrance = [entrancerow, entrancecol] 表示你一开始所在格子的行和列。
每一步操作，你可以往 上，下，左 或者 右 移动一个格子。你不能进入墙所在的格子，你也不能离开迷宫。你的目标是找到离 entrance 最近 的出口。出口 的含义是 maze 边界 上的 空格子。entrance 格子 不算 出口。
请你返回从 entrance 到最近出口的最短路径的 步数 ，如果不存在这样的路径，请你返回 -1 。
在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：
值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。
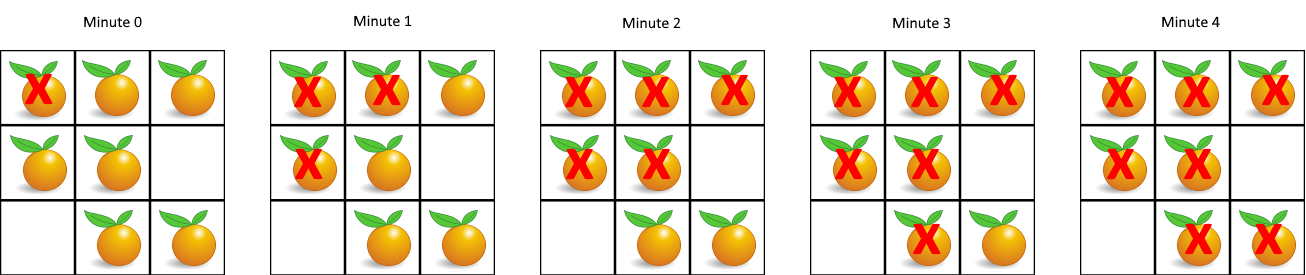
每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。
如果不可能，返回 -1 。
示例 1：
大家好，我是老马。
今天我们一起来学习一下数组这种数据结构。
数组需要拆分下面几个部分：
理论介绍
源码分析
数据结构实现？
题目练习（按照算法思想分类）
梳理对应的 sdk 包
应用实战
因为这个是 leetcode 系列，所以重点是 4、5(对4再一次总结)。
为了照顾没有基础的小伙伴，会简单介绍一下1的基础理论。