LC994. 腐烂的橘子 rotting-oranges
LC994. 腐烂的橘子 rotting-oranges
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。
如果不可能,返回 -1 。
示例 1:
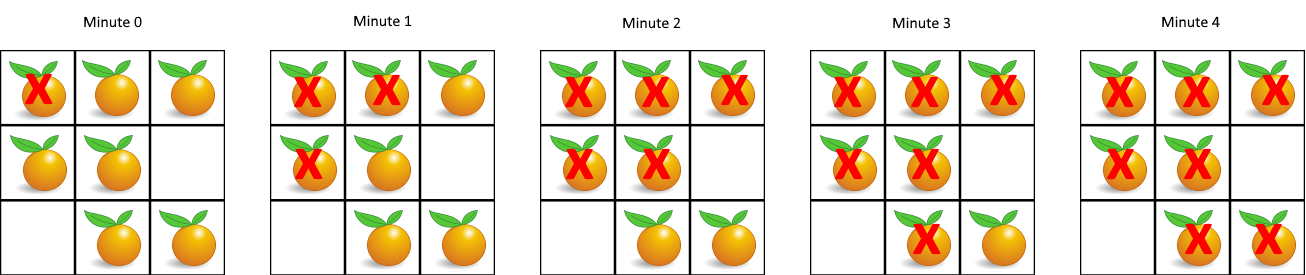
输入:grid = [[2,1,1],[1,1,0],[0,1,1]]
输出:4
示例 2:
输入:grid = [[2,1,1],[0,1,1],[1,0,1]]
输出:-1
解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个方向上。
示例 3:
输入:grid = [[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 10
grid[i][j] 仅为 0、1 或 2
v1-DFS
思路
老规矩,图问题先上一个 DFS。
注意的是,这里的开始位置有多个,每一个腐烂的橘子都要作为开始位置。
DFS 由于其是全局遍历,所以我们最好用一个额外的数组,记录一下耗时。
int[x][y] 记录每一个点的腐烂耗时,初始化为最大值,表示不可达(不会被腐烂)。
最后的结果就是遍历这个数组,看一下非0的位置,找到有效最大值即可。
实现
class Solution {
int[][] dirs = {{1,0}, {-1,0}, {0,1}, {0,-1}};
int m = 0;
int n = 0;
public int orangesRotting(int[][] grid) {
m = grid.length;
n = grid[0].length;
int[][] time = new int[m][n];
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
time[i][j] = Integer.MAX_VALUE;
}
}
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
if(grid[i][j] == 2) {
dfs(grid, time, i, j, 0);
}
}
}
int res = 0;
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
if(grid[i][j] == 0) {
continue;
}
if(time[i][j] == Integer.MAX_VALUE) {
// 存在未感染的点
return -1;
} else {
res = Math.max(res, time[i][j]);
}
}
}
return res;
}
private void dfs(int[][] grid, int[][] time, int x, int y, int t) {
// 终止
if(x < 0 || y < 0 || x >= m || y >= n || grid[x][y] == 0) {
return;
}
// 时间是否有效 已经被感染过的跳过
if(t > time[x][y]) {
return;
}
// 更新时间 为了不影响后续操作,不变更状态信息
time[x][y] = t;
// 递归
for(int[] dir : dirs) {
int nx = x + dir[0];
int ny = y + dir[1];
dfs(grid, time, nx, ny, t+1);
}
}
}效果
4ms 击败 3.18%
反思
当然,这种最合适的还是 bfs。
v2-BFS+染色
思路
这种求最短的场景,其实还是 BFS 比较自然。
因为 BFS 是逐层展开,满足条件时,就是最短。
避免了 DFS 的大量无效的路径。
这里 visited 数组不是必须,我们直接用染色替代。
实现
class Solution {
public int orangesRotting(int[][] grid) {
int[][] dirs = {{1,0}, {-1, 0}, {0,1}, {0,-1}};
int m = grid.length;
int n = grid[0].length;
Queue<int[]> queue = new LinkedList<>();
// 新鲜的数量
int freshCount = 0;
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
// 腐烂
if(grid[i][j] == 2) {
queue.offer(new int[]{i, j});
} else if(grid[i][j] == 1){
freshCount++;
}
}
}
// 没有fresh
if(freshCount <= 0) {
return 0;
}
// 没腐烂
if(queue.isEmpty()) {
return -1;
}
int t = 0;
while(!queue.isEmpty()) {
int size = queue.size();
for(int i = 0; i < size; i++) {
int[] cur = queue.poll();
int x = cur[0];
int y = cur[1];
if(grid[x][y] == 1) {
grid[x][y] = 2;
freshCount--;
if(freshCount <= 0) {
return t;
}
}
// 子节点迭代
for(int[] dir : dirs) {
int nx = x + dir[0];
int ny = y + dir[1];
// 终止
if(nx < 0 || ny < 0 || nx >= m || ny >= n || grid[nx][ny] != 1) {
continue;
}
queue.offer(new int[]{nx, ny});
}
}
// 时间增加
t++;
}
// 不可达
return -1;
}
}效果
2ms 击败 37.60%
优化1-避免重复
重复入队列
这里其实有一个问题,被 queue 的自动扩容隐藏起来了。
那就是一个橘子可能在不同的路径被重复感染入队列。
如何解决呢?
我们可以在队列的时候就设置为腐烂。
之所以在意这个,是为了我们后续数组压缩做准备。
实现
class Solution {
public int orangesRotting(int[][] grid) {
int[][] dirs = {{1,0}, {-1, 0}, {0,1}, {0,-1}};
int m = grid.length;
int n = grid[0].length;
Queue<int[]> queue = new LinkedList<>();
// 新鲜的数量
int freshCount = 0;
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
// 腐烂
if(grid[i][j] == 2) {
queue.offer(new int[]{i, j});
} else if(grid[i][j] == 1){
freshCount++;
}
}
}
// 没有fresh
if(freshCount <= 0) {
return 0;
}
int t = 0;
while(!queue.isEmpty()) {
int size = queue.size();
// 是否存在感染
boolean affectFlag = false;
for(int i = 0; i < size; i++) {
int[] cur = queue.poll();
int x = cur[0];
int y = cur[1];
// 子节点迭代
for(int[] dir : dirs) {
int nx = x + dir[0];
int ny = y + dir[1];
// 终止
if(nx < 0 || ny < 0 || nx >= m || ny >= n || grid[nx][ny] != 1) {
continue;
}
grid[nx][ny] = 2;
freshCount--;
affectFlag = true;
queue.offer(new int[]{nx, ny});
}
}
// 时间增加 可能有一轮没有新增感染
if(affectFlag) {
t++;
}
}
// 不可达
return freshCount == 0 ? t : -1;
}
}效果
耗时变化不大
2ms 击败 37.60%
v3-一维数组压缩
思路
类似 LC1926,我们可以进行一维数组压缩。
避免 int[] 对象的创建 + queue 队列的消耗。
int[] queue = new int[m*n];每一个点的位置,可以用 val = m*n + y 来表示
出队列的时候,还原
x = val / n;
y = val % n;实现
class Solution {
public int orangesRotting(int[][] grid) {
int[][] dirs = {{1,0}, {-1, 0}, {0,1}, {0,-1}};
int m = grid.length;
int n = grid[0].length;
int[] queue = new int[m*n];
int head = 0;
int tail = 0;
// 新鲜的数量
int freshCount = 0;
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
// 腐烂
if(grid[i][j] == 2) {
queue[tail++] = n*i + j;
} else if(grid[i][j] == 1){
freshCount++;
}
}
}
// 没有fresh
if(freshCount <= 0) {
return 0;
}
int t = 0;
while(tail > head) {
int size = tail-head;
// 是否存在感染
boolean affectFlag = false;
for(int i = 0; i < size; i++) {
int cur = queue[head++];
int x = cur / n;
int y = cur % n;
// 子节点迭代
for(int[] dir : dirs) {
int nx = x + dir[0];
int ny = y + dir[1];
// 终止
if(nx < 0 || ny < 0 || nx >= m || ny >= n || grid[nx][ny] != 1) {
continue;
}
grid[nx][ny] = 2;
freshCount--;
affectFlag = true;
queue[tail++] = n*nx + ny;
}
}
// 时间增加 可能有一轮没有新增感染
if(affectFlag) {
t++;
}
}
// 不可达
return freshCount == 0 ? t : -1;
}
}效果
1ms 击败 99.97%
反思
还能更快吗?
