LC701. 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。

返回插入后二叉搜索树的根节点。

输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。

你可以返回 任意有效的结果 。

示例 1：

1

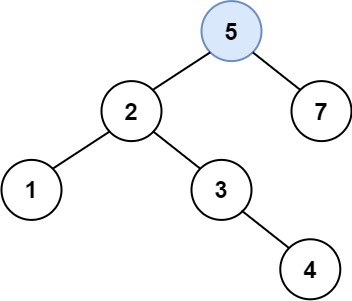
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

示例 2：

2

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

提示：

树中的节点数将在 [0, 10^4]的范围内。
-10^8 <= Node.val <= 10^8
所有值 Node.val 是 独一无二 的。
-10^8 <= val <= 10^8
保证 val 在原始BST中不存在。

v1-递归

思路

插入，和 LC700 的搜索非常类似。

依然是递归

如果 val < root.val → 插到左子树。

如果 val > root.val → 插到右子树。

如果子树是空的，就在这里建一个新节点。

实现

    public TreeNode insertIntoBST(TreeNode root, int val) {
        if(root == null) {
            return new TreeNode(val);
        }

        // left
        if(val < root.val) {
            root.left = insertIntoBST(root.left, val);
        } else {
            root.right = insertIntoBST(root.right, val);
        }

        return root;
    }

效果

0ms 100%

复杂度

时间复杂度：O(h)，平均 O(log n)，最坏 O(n)

空间复杂度：O(h)，平均 O(log n)，最坏 O(n)

v2-迭代

思路

类似的，我们可以用迭代来实现这个功能。

迭代看起来其实也不难。

实现

public TreeNode insertIntoBST(TreeNode root, int val) {
    if(root == null) {
        return new TreeNode(val);
    }

    TreeNode cur = root;
    while(true) {
        // 小于，则插入到左边    
        if(val < cur.val) {
            TreeNode left = cur.left;
            // 直接创建
            if(left == null) {
                cur.left = new TreeNode(val);        
                break;
            } else {
                // 继续往左找
                cur = left;
            }
        }

        // 节点独一无二，所以不会相等
        if(val > cur.val) {
            TreeNode right = cur.right;
            // 直接创建
            if(right == null) {
                cur.right = new TreeNode(val);        
                break;
            } else {
                // 继续往右找
                cur = right;
            }
        }
    }

    // 返回根
    return root;
}

效果

0ms 100%

复杂度

时间复杂度：O(h)（树高，平均 O(log n)，最坏 O(n)）

空间复杂度：O(1)（相比递归的 O(h) 节省了栈空间）

反思

迭代法看起来没有递归优雅，但是更加有助于我们理解。

如果题目要求空间限制，那么是不错的解法。

还是建议，以后给出递归+迭代两个版本实现。

参考资料