LC1372. 二叉树中的最长交错路径 longest-zigzag-path-in-a-binary-tree

给你一棵以 root 为根的二叉树，二叉树中的交错路径定义如下：

选择二叉树中 任意 节点和一个方向（左或者右）。
如果前进方向为右，那么移动到当前节点的的右子节点，否则移动到它的左子节点。
改变前进方向：左变右或者右变左。
重复第二步和第三步，直到你在树中无法继续移动。
交错路径的长度定义为：访问过的节点数目 - 1（单个节点的路径长度为 0 ）。

请你返回给定树中最长 交错路径 的长度。

示例 1：

1

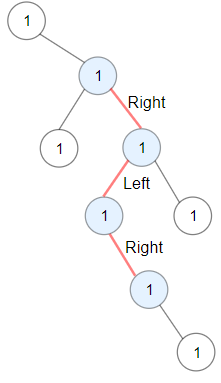
输入：root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
输出：3
解释：蓝色节点为树中最长交错路径（右 -> 左 -> 右）。

示例 2：

2

输入：root = [1,1,1,null,1,null,null,1,1,null,1]
输出：4
解释：蓝色节点为树中最长交错路径（左 -> 右 -> 左 -> 右）。

示例 3：

输入：root = [1]
输出：0

提示：

每棵树最多有 50000 个节点。
每个节点的值在 [1, 100] 之间。

v1-DFS 暴力

思路

这里的左到右，右到左。实现起来也不难，我们加一个变量控制就行。

任意节点的话，我们先用暴力的方式，整体遍历这棵树，然后从遍历的位置继续重复刚才的操作。

当然，性能很差，只是为了方便大家理解。

实现

class Solution {
    private int max = 0;
    public int longestZigZag(TreeNode root) {
        travelTree(root);
        return max;
    }

    // 任意节点
    private void travelTree(TreeNode root) {
        if(root == null) {
            return;
        }

        // 尝试左右
        dfs(root, 0, true);
        dfs(root, 0, false);

        // 递归子树
        travelTree(root.left);
        travelTree(root.right);
    }

    private void dfs(TreeNode node, int count, boolean leftDirection) {
        if(node == null) {
            return;
        }

        // 经过当前节点
        count++;
        int len = count-1;
        if(len > max) {
            max = len;
        }

        // 左->右
        if(leftDirection) {
            dfs(node.left, count, false);
        } 

        // 右->左
        if(!leftDirection) {
            dfs(node.right, count, true);
        } 
    }

}

效果

超出时间限制

56 / 58 个通过的测试用例

复杂度

时间复杂度：

平衡树 H ≈ log N → O(N log N)

最坏情况（链状树）H ≈ N → O(N²)

反思

这里会大量的重复遍历。

如何优化呢？

v2-一次 DFS

思路

我们可以在 v1 的基础之上，少走回头路。

我们直接从 root.left, root.right 开始，此时 count=1 计算。因为已经走了一步了。

// 尝试左右
dfs(root.left, 1, true);   // 从根节点左子节点开始，左方向
dfs(root.right, 1, false); // 从根节点右子节点开始，右方向

如何避免重复走呢？下面是重点

if (leftDirection) {
    // 左 -> 右
    dfs(node.right, count + 1, false); // 持续 ZigZag
    dfs(node.left, 1, true);           // 重新开始
} else {
    // 右 -> 左
    dfs(node.left, count + 1, true);   // 持续 ZigZag
    dfs(node.right, 1, false);         // 重新开始
}

这里的好处在于可以用当前节点直接出发，还不是 v1 的出头再来。

实现

class Solution {
    private int max = 0;

    public int longestZigZag(TreeNode root) {
        if (root == null) return 0;

        // 尝试左右
        dfs(root.left, 1, true);   // 从根节点左子节点开始，左方向
        dfs(root.right, 1, false); // 从根节点右子节点开始，右方向

        return max;
    }

    private void dfs(TreeNode node, int count, boolean leftDirection) {
        if (node == null) return;

        // 更新最大值
        max = Math.max(max, count);

        if (leftDirection) {
            // 左 -> 右
            dfs(node.right, count + 1, false); // 持续 ZigZag
            dfs(node.left, 1, true);           // 重新开始
        } else {
            // 右 -> 左
            dfs(node.left, count + 1, true);   // 持续 ZigZag
            dfs(node.right, 1, false);         // 重新开始
        }
    }
}

效果

6ms 击败 90.61%

反思

这个实际已经是最优秀，看了最佳解法，一样的。

参考资料