LC1161. 最大层内元素和 maximum-level-sum-of-a-binary-tree

给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层，而根节点的子节点位于第 2 层，依此类推。

请返回层内元素之和 最大 的那几层（可能只有一层）的层号，并返回其中 最小 的那个。

示例 1：

1

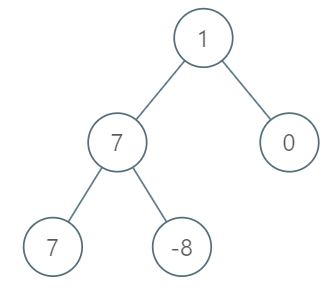
输入：root = [1,7,0,7,-8,null,null]
输出：2
解释：
第 1 层各元素之和为 1，
第 2 层各元素之和为 7 + 0 = 7，
第 3 层各元素之和为 7 + -8 = -1，
所以我们返回第 2 层的层号，它的层内元素之和最大。

示例 2：

输入：root = [989,null,10250,98693,-89388,null,null,null,-32127]

输出：2

提示：

树中的节点数在 [1, 10^4]范围内

-10^5 <= Node.val <= 10^5

v1-DFS

思路

计算每一层的最大和。

最底层的基础还是层序遍历。

我们先用最简单的思路，把每一层的结果都记录下来，然后比较大小。

当然，这个比较慢，只是方便大家理解。

实现

class Solution {

    public int maxLevelSum(TreeNode root) {
        List<List<Integer>> allList = new ArrayList<>();     
        dfs(root, allList, 0);

        int maxLevel = 0;
        long maxVal = root.val;

        for(int i = 0; i < allList.size(); i++) {
            List<Integer> levels = allList.get(i);

            // 计算和
            long sum = 0;
            for(Integer val : levels) {
                sum += val;
            }
            if(sum > maxVal) {
                maxVal = sum;
                maxLevel = i;
            }
        }

        // 结果从1开始
        return maxLevel+1;   
    }

    private void dfs(TreeNode node, List<List<Integer>> allList, int level) {
        if(node == null) {
            return;
        }

        if(level >= allList.size()) {
            allList.add(new ArrayList<>());
        }
        // 添加当前元素
        allList.get(level).add(node.val);

        dfs(node.left, allList, level+1);
        dfs(node.right, allList, level+1);
    }

}

效果

13ms 击败 7.89%

反思

之所以比较慢，是实际上我们不太需要记录全部的结果。

我们可以在遍历的时候就把结果计算出来。

优化1-只记录和

我们不需要记录每一层的具体信息，只需要每一层的累加和即可

实现

public int maxLevelSum(TreeNode root) {
        List<Long> allList = new ArrayList<>();     
        dfs(root, allList, 0);

        int maxLevel = 0;
        long maxVal = root.val;

        for(int i = 0; i < allList.size(); i++) {
            Long sum = allList.get(i);
            if(sum > maxVal) {
                maxVal = sum;
                maxLevel = i;
            }
        }

        // 结果从1开始
        return maxLevel+1;   
    }

    private void dfs(TreeNode node, List<Long> allList, int level) {
        if(node == null) {
            return;
        }

        // 新的一层
        if(level >= allList.size()) {
            allList.add(0L);
        }

        // 添加当前元素
        Long pre = allList.get(level);
        allList.set(level, pre+node.val);

        dfs(node.left, allList, level+1);
        dfs(node.right, allList, level+1);
    }

效果

7ms 击败 91.42%

这样就快了很多。

优化2-dfs 数组模拟

思路

我们用数组模拟实现 list。

避免 ArrayList 开销，和一些类型的装箱、拆箱。

实现

class Solution {

    
    private int treeLevel = 0;

    public int maxLevelSum(TreeNode root) {
        long[] allList = new long[100];     
        dfs(root, allList, 0);

        int maxLevel = 0;
        long maxVal = root.val;

        for(int i = 0; i <= treeLevel; i++) {
            long sum = allList[i];
            if(sum > maxVal) {
                maxVal = sum;
                maxLevel = i;
            }
        }

        // 结果从1开始
        return maxLevel+1;   
    }

    private void dfs(TreeNode node, long[] allList, int level) {
        if(node == null) {
            return;
        }

        // 更新一下，避免不知道有多少层
        if(level >= treeLevel) {
            treeLevel = level;
        }

        // 添加当前元素
        allList[level] += node.val;

        dfs(node.left, allList, level+1);
        dfs(node.right, allList, level+1);
    }

}

效果

3ms 100%

效果拔群！

果然，还的是数组。

v2-BFS

思路

老规矩，复习一下 BFS 的写法。

实现

    public int maxLevelSum(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>(); 
        queue.offer(root);

        long maxLevelSum = Long.MIN_VALUE;
        int maxLevel = 1;
        // 记录层级
        int level=0;

        while(!queue.isEmpty()) {
            level++;
            int size = queue.size();

            // 这一层
            long sum = 0;
            for(int i = 0; i < size; i++) {
                TreeNode node = queue.poll();
                sum += node.val;

                // 子节点入队列
                if(node.left != null) {
                    queue.offer(node.left);
                }
                if(node.right != null) {
                    queue.offer(node.right);
                }
            }

            // 更新 max
            if(sum > maxLevelSum) {
                maxLevelSum = sum;
                maxLevel = level;
            }
        }

        return maxLevel;
    }

效果

9ms 击败 43.22%

反思

整体实现没有任何问题。

只要还是在于 queue 的创建消耗。

优化1-数组模拟

思路

我们用 array 来模拟实现一个 queue。

看下题目条件，节点数是有限制的，最大 10000。

实现

class Solution {

    public int maxLevelSum(TreeNode root) {
        int queueHead = 0;
        int queueTail = 0;
        TreeNode[] queue = new TreeNode[10000]; 
        queue[queueTail++] = root;

        long maxLevelSum = Long.MIN_VALUE;
        int maxLevel = 1;
        // 记录层级
        int level=0;

        while(queueTail > queueHead) {
            level++;
            int size = queueTail - queueHead;

            // 这一层
            long sum = 0;
            for(int i = 0; i < size; i++) {
                TreeNode node = queue[queueHead++];
                sum += node.val;

                // 子节点入队列
                if(node.left != null) {
                    queue[queueTail++] = node.left;
                }
                if(node.right != null) {
                    queue[queueTail++] = node.right;
                }
            }

            // 更新 max
            if(sum > maxLevelSum) {
                maxLevelSum = sum;
                maxLevel = level;
            }
        }

        return maxLevel;
    }
    
}

效果

5ms 击败 98.63%

反思

数组还是开辟的太大了，可以小一点的。

不过这样还是要考虑下标的滚动之类的。

参考资料