LC199. 二叉树的右视图 binary-tree-right-side-view

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1：

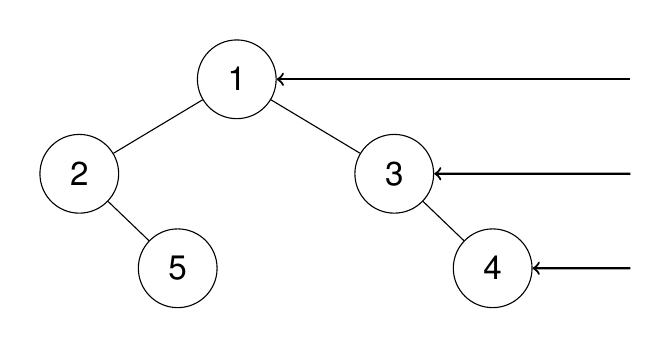
输入：root = [1,2,3,null,5,null,4]

输出：[1,3,4]

解释：

1

示例 2：

输入：root = [1,2,3,4,null,null,null,5]

输出：[1,3,4,5]

解释：

2

示例 3：

输入：root = [1,null,3]

输出：[1,3]

示例 4：

输入：root = []

输出：[]

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

v1-DFS

思路

所谓左右视图，本质上就是层序遍历。

左视图，取每一层的第一个元素；

右视图，取每一层的最后一个元素。

实现

public List<Integer> rightSideView(TreeNode root) {
        List<List<Integer>> allList = new ArrayList<>();    
        dfs(root, allList, 0);

        // 构建结果
        List<Integer> res = new ArrayList<>();    
        for(List<Integer> levels : allList) {
            res.add(levels.get(levels.size()-1));
        }
        return res;
    }

    private void dfs(TreeNode node, List<List<Integer>> list, int level) {
        if(node == null) {
            return;
        }

        // 判断是否为新的一层
        if(level >= list.size()) {
            list.add(new ArrayList<>());
        }
        list.get(level).add(node.val);

        // 递归
        dfs(node.left, list, level+1);
        dfs(node.right, list, level+1);
    }

效果

1ms 击败 74.45%

反思

上面的写法主要是为了直接复用层序遍历，我们可以适当优化一下。

我们可以不用 list 记录所有的元素，但是递归子树的时候，要先看右边节点。这样第一层的元素，第一次遇到的实际上就是右边视图的。

优化实现

    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        dfs(root, res, 0);
        return res;
    }

    private void dfs(TreeNode node, List<Integer> res, int level) {
        if (node == null) return;

        // 第一次到达这个层，直接加入节点
        if (level == res.size()) {
            res.add(node.val);
        }

        // 先右后左
        dfs(node.right, res, level + 1);
        dfs(node.left, res, level + 1);
    }

效果

1ms 击败 74.45%

反思

这个只是用例没有体现出来，本质上对象的创建已经少了很多。

v2-BFS

广度优先思路

类似的，我们可以用 queue 实现广度优先层序遍历。

我们可以直接先实现 levelOrder，然后用类似 v1 的取法即可。

每一层的最后一个元素直接入结果 list 就行。

实现

    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null) {
            return res;
        }
        
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while(!queue.isEmpty()) {
            int size = queue.size();

            for(int i = 0; i < size; i++) {
                TreeNode node = queue.poll();
                // 最右边一个元素放入结果
                if(i == size - 1) {
                    res.add(node.val);
                }

                // 子节点入队列
                if(node.left != null) {
                    queue.offer(node.left);
                }
                if(node.right != null) {
                    queue.offer(node.right);
                }
            }
        }

        return res;
    }

效果

1ms 击败 74.45%

反思

看了一下最优解法，是一样的。

参考资料