跳至主要內容

LC1466. 重新规划路线 reorder-routes-to-make-all-paths-lead-to-the-city-zero

老马啸西风2025年9月30日大约 5 分钟Leetcode-75leetcodeLeetcode-75graphdfsbfs

LC1466. 重新规划路线 reorder-routes-to-make-all-paths-lead-to-the-city-zero

n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。

路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。

今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。

请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。

题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。

示例 1：

1
1

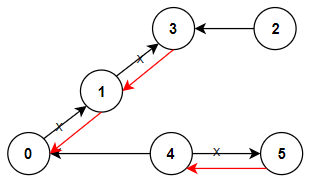
输入：n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
输出：3
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。
示例 2：

2
2

输入：n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
输出：2
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。
示例 3：

输入：n = 3, connections = [[1,0],[2,0]]
输出：0

提示：

2 <= n <= 5 * 10^4
connections.length == n-1
connections[i].length == 2
0 <= connections[i][0], connections[i][1] <= n-1
connections[i][0] != connections[i][1]

v1-DFS

思路

这一题题目指定的是有向图，a->b

但是我们想解决问题，实际上要考虑的是从 0 从发，DFS 的无向图。

然后发现如果实际反向和预期的方向相反，说明这个路需要调整。

实现

这里主要是为了方便阅读，所以用来 HashMP+对象的方式

class Solution {

    private class Node {
        public int target;
        public int dir;
        public Node(int target, int dir) {
            this.target = target;
            this.dir = dir;
        }
    }
    // 结果
    private int res = 0;
    public int minReorder(int n, int[][] connections) {
        // 构建无向图
        Map<Integer, List<Node>> graph = new HashMap<>();
        for(int i = 0; i < connections.length; i++) {
            int[] conn = connections[i];
            int from = conn[0];
            int target = conn[1];
            // 顺
            Node node1 = new Node(target, 1);
            List<Node> list1 = graph.getOrDefault(from, new ArrayList<>());
            list1.add(node1);
            graph.put(from, list1);

            // 逆
            Node node2 = new Node(from, 0);
            List<Node> list2 = graph.getOrDefault(target, new ArrayList<>());
            list2.add(node2);
            graph.put(target, list2);
        }

        // dfs
        boolean[] visited = new boolean[n];
        dfs(graph, visited, 0);
        return res;
    }

    private void dfs(Map<Integer, List<Node>> graph, boolean[] visited, int i) {
        if(visited[i]) {
            return;
        }
        // 设置
        visited[i] = true;

        // 邻居
        List<Node> ns = graph.get(i);
        if(ns != null) {
            for(Node node : ns) {
                int target = node.target;
                if(!visited[target]) {
                    // 累加
                    res += node.dir;
                    dfs(graph, visited, target);
                }
            }
        }
    }
}

顺路的时候，0->x 说明是从 0 开始顺路，此时是需要+1的。因为预期是期望从 x->0

效果

94ms 击败 12.28%

复杂度

时间复杂度：O(n)

空间复杂度（递归栈）：O(n)。

反思

复杂度本身并没有毛病。

为什么慢？

引入了对象创建+HashMap

v2-数组

思路

原生的数组性能要比 HashMap 好很多，我们来实现一下。

整体方法不变，知识把 HashMap 改为数组。

实现

class Solution {

    private class Node {
        public int target;
        public int dir;
        public Node(int target, int dir) {
            this.target = target;
            this.dir = dir;
        }
    }
    // 结果
    private int res = 0;
    public int minReorder(int n, int[][] connections) {
        // 构建无向图(j 数组为动态大小)
        Node[][] graph = new Node[n][];
        int[] degree = new int[n];
        for(int[] conn : connections) {
            degree[conn[0]]++;
            degree[conn[1]]++;
        }
        for(int i = 0; i < n; i++) {
            int size = degree[i];
            graph[i] = new Node[size];
        }

        // 无向图构建
        int[] ixArray = new int[n]; // 记录下标
        for(int[] conn : connections) {
            int from = conn[0];
            int target = conn[1];
            // 顺
            Node node1 = new Node(target, 1);
            graph[from][ixArray[from]++] = node1;

            // 逆
            Node node2 = new Node(from, 0);
            graph[target][ixArray[target]++] = node2;
        }

        // dfs
        boolean[] visited = new boolean[n];
        dfs(graph, visited, 0);
        return res;
    }

    private void dfs(Node[][] graph, boolean[] visited, int i) {
        if(visited[i]) {
            return;
        }
        // 设置
        visited[i] = true;

        // 邻居
        Node[] ns = graph[i];
        if(ns != null) {
            for(Node node : ns) {
                int target = node.target;
                if(!visited[target]) {
                    // 累加
                    res += node.dir;
                    dfs(graph, visited, target);
                }
            }
        }
    }
}

效果

19ms 击败 98.72%

反思

当然，感觉这里还是有优化空间。

比如这个数组的创建。

v1-Node 替代

思路

当然对象的创建也可以简化，这个是为了方便大家阅读。

Node 完全可以用 int[2] 数组替代

实现

class Solution {

    // 结果
    private int res = 0;

    public int minReorder(int n, int[][] connections) {
        // 构建无向图（数组形式）
        int[][][] graph = new int[n][][];
        int[] degree = new int[n];

        // 统计每个节点的度数
        for (int[] conn : connections) {
            degree[conn[0]]++;
            degree[conn[1]]++;
        }

        // 初始化每个节点的邻接表
        for (int i = 0; i < n; i++) {
            graph[i] = new int[degree[i]][2]; // 每条边存 [target, dir]
        }

        // 填充邻接表
        int[] idx = new int[n]; // 当前下标
        for (int[] conn : connections) {
            int from = conn[0], to = conn[1];

            // 正向边（from -> to），需要翻转
            graph[from][idx[from]++] = new int[]{to, 1};

            // 反向边（to -> from），不需要翻转
            graph[to][idx[to]++] = new int[]{from, 0};
        }

        // DFS 遍历
        boolean[] visited = new boolean[n];
        dfs(graph, visited, 0);

        return res;
    }

    private void dfs(int[][][] graph, boolean[] visited, int u) {
        if (visited[u]) return;
        visited[u] = true;

        for (int[] edge : graph[u]) {
            int v = edge[0], dir = edge[1];
            if (!visited[v]) {
                res += dir;
                dfs(graph, visited, v);
            }
        }
    }
}

效果

42ms 击败 48.85%

竟然下降了？

猜测原因：

版本特性常数开销
Node[][]对象字段访问，JVM 可优化内联较小
int[][][]三维数组访问 + 多次边界检查稍大
ArrayList<int[]>[]动态数组，数组引用 + 对象引用介于两者

v2-ArrayList 替代 array

思路

数组中有一个 array 的大小计算，很麻烦。

如果用 list 替代，可以不关心。

但是性能略微下降，不过书写时更不容易出错。

实现

class Solution {

    private class Node {
        public int target;
        public int dir;
        public Node(int target, int dir) {
            this.target = target;
            this.dir = dir;
        }
    }

    private int res = 0;

    public int minReorder(int n, int[][] connections) {
        // 用 ArrayList 替代二维数组
        ArrayList<Node>[] graph = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }

        // 构建图
        for (int[] conn : connections) {
            int from = conn[0], to = conn[1];

            // 正向边 (from -> to) 需要翻转
            graph[from].add(new Node(to, 1));

            // 反向边 (to -> from) 不需要翻转
            graph[to].add(new Node(from, 0));
        }

        // DFS
        boolean[] visited = new boolean[n];
        dfs(graph, visited, 0);

        return res;
    }

    private void dfs(ArrayList<Node>[] graph, boolean[] visited, int u) {
        visited[u] = true;
        for (Node node : graph[u]) {
            int v = node.target;
            if (!visited[v]) {
                res += node.dir;
                dfs(graph, visited, v);
            }
        }
    }
}

效果

31ms 击败 95.91%

实际比赛，还是推荐大家用 list 的方式，避免踩坑。

参考资料

贡献者

bbhou
我是老马，期待与你的下次重逢
Copyright © 2025 老马啸西风