LC700. 二叉搜索树中的搜索 search-in-a-binary-search-tree

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

示例 1:

1

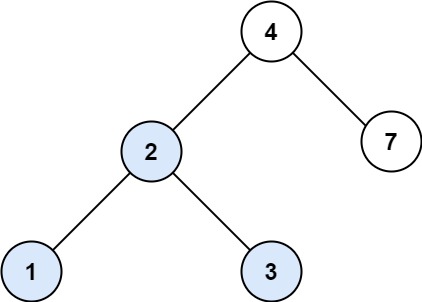
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

2

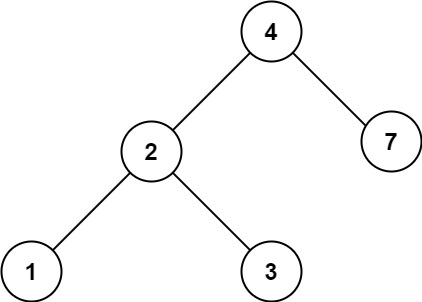
输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

树中节点数在 [1, 5000] 范围内
1 <= Node.val <= 10^7
root 是二叉搜索树
1 <= val <= 10^7

v1-递归

思路

因为 BST 的特性，和二分法差不多。

实现也很简单。

实现

public TreeNode searchBST(TreeNode root, int val) {
        // 递归即可
        if(root == null) {
            return null;
        }       
        if(root.val == val) {
            return root;
        }
        if(val > root.val) {
            // 看右边
            return searchBST(root.right, val);
        }
        return searchBST(root.left, val);
}

效果

0ms 100%

复杂度

时间复杂度：O(h)，平均 O(log n)，最坏 O(n)

空间复杂度：O(h)，平均 O(log n)，最坏 O(n)

反思

没有太大区分度。

BST 本身这个数据结构还是比较重要的。

v2-迭代

思路

同理，我们可以通过迭代来实现。

实现

public TreeNode searchBST(TreeNode root, int val) {
        // 递归即可
        if(root == null) {
            return null;
        }       
        
        // 不为空
        TreeNode cur = root;
        while(cur != null) {
            if(cur.val == val) {
                return cur;
            } else if(cur.val < val) {
                // 当前小，去右边
                cur = cur.right;
            } else {
                cur = cur.left;
            }
            
        }

        // NOT-FOUND
        return null;
}

效果

0ms 100%

复杂度

时间复杂度：O(h)，平均 O(log n)，最坏 O(n)

空间复杂度：O(1)

反思

针对空间限制，迭代的解法其实更好。

最好是同时掌握二者。

参考资料