题目
城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度,请返回 由这些建筑物形成的 天际线 。
每个建筑物的几何信息由数组 buildings 表示,其中三元组 buildings[i] = [lefti, righti, heighti] 表示:
lefti 是第 i 座建筑物左边缘的 x 坐标。
righti 是第 i 座建筑物右边缘的 x 坐标。
heighti 是第 i 座建筑物的高度。
你可以假设所有的建筑都是完美的长方形,在高度为 0 的绝对平坦的表面上。
天际线 应该表示为由 “关键点” 组成的列表,格式 [[x1,y1],[x2,y2],…] ,并按 x 坐标 进行 排序 。
关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点,y 坐标始终为 0 ,仅用于标记天际线的终点。此外,任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。
注意:输出天际线中不得有连续的相同高度的水平线。例如 […[2 3], [4 5], [7 5], [11 5], [12 7]…] 是不正确的答案;三条高度为 5 的线应该在最终输出中合并为一个:[…[2 3], [4 5], [12 7], …]
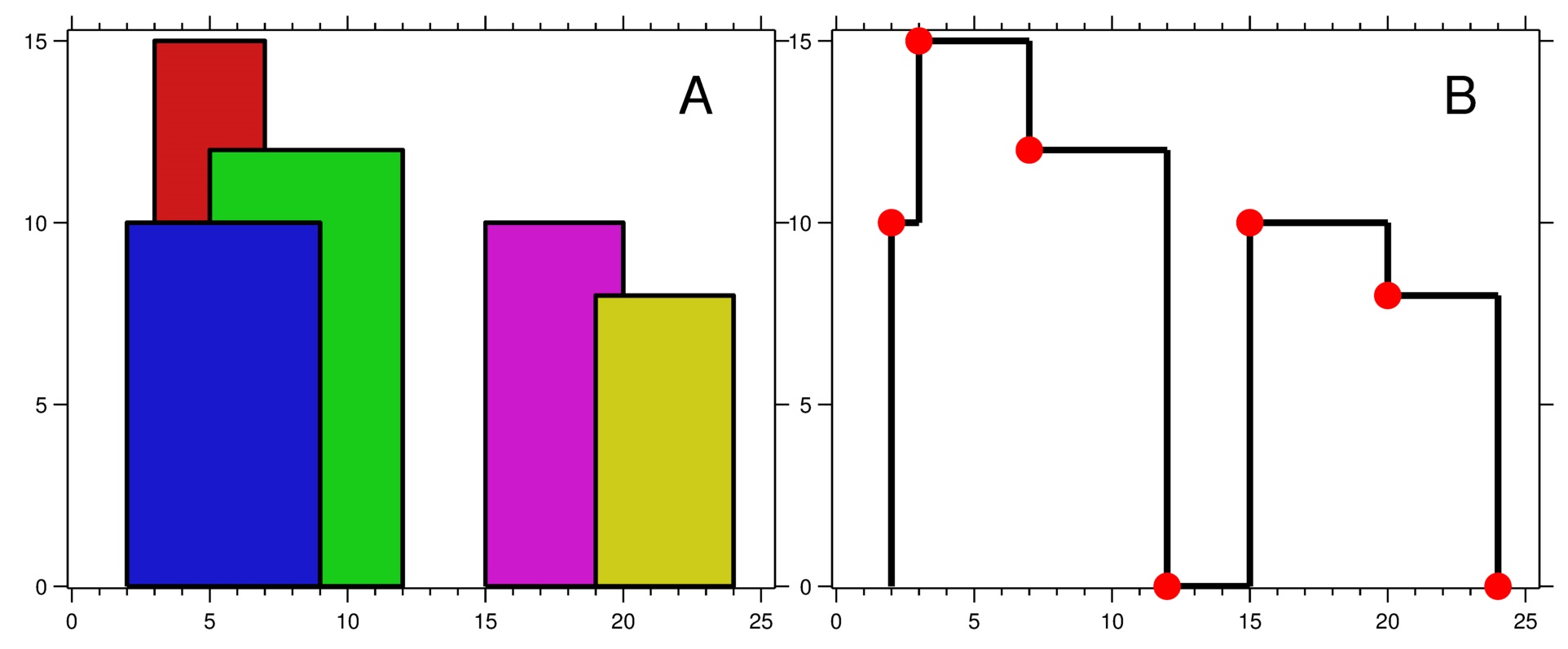
输入:buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]] 输出:[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释:
图 A 显示输入的所有建筑物的位置和高度,
图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。
示例 2:
输入:buildings = [[0,2,3],[2,5,3]] 输出:[[0,3],[5,0]]
提示:
1 <= buildings.length <= 10^4 0 <= lefti < righti <= 2^31 - 1 1 <= heighti <= 2^31 - 1 buildings 按 lefti 非递减排序
思路分析?
直接看这篇,写的很不错。
v1-简单思路
思路
虽然说思路是一样的,但是我们这里不利用复杂的数据结构,让读者理解我们为什么要一步步这么做。
1)把所有的矩形抽象为左上角(x_left, high)、右上角(x_right, high)
2) 影响天际线的是什么?
矩形的左上角进入,则产生影响开始;矩形的右上角离开,产生的影响结束。
所以我们需要区分左右,可以额外添加一个标识,也可以直接利用正负值来区分(扫描线)
3)按照 x 排序
优先 x 小的在前面,如果 x 相同:
考虑两个坐标比较的时候,x 坐标相等会有三种情况。
-
当两个坐标都是左上角坐标,我们要将高度高的排在前边
-
当两个坐标都是右上角坐标,我们要将高度低的排在前边
-
当两个坐标一个是左上角坐标,一个是右上角坐标,我们需要将左上角坐标排在前边
核心步骤拆分
左右定点初始化
// 存储所有的坐标点(建筑物的左边界和右边界)
List<List<Integer>> points = new ArrayList<>();
// 提取每个建筑物的左边界和右边界
for (int[] b : buildings) {
// 左边界,y 为负数表示开始
List<Integer> p1 = new ArrayList<>();
p1.add(b[0]);
p1.add(-b[2]);
points.add(p1);
// 右边界,y 为正数表示结束
List<Integer> p2 = new ArrayList<>();
p2.add(b[1]);
p2.add(b[2]);
points.add(p2);
}
排序
按照上面的规则
// 对所有坐标点按照 x 坐标排序,x 相同则按 y 排序
Collections.sort(points, (p1, p2) -> {
int x1 = p1.get(0);
int y1 = p1.get(1);
int x2 = p2.get(0);
int y2 = p2.get(1);
if (x1 != x2) {
return x1 - x2; // x 排序
} else {
return y1 - y2; // y 排序
}
});
更新
遍历所有的 x 节点
1) 获取对应的 y
a. y < 0,则为左顶点,开始产生影响。加入高度列表
b. y > 0,则为有顶点,结束产生影响。从高度列表移除
2)高度列表排序,方便 get(0) 获取高度最高的 height
3) 如果 height > preHeight。
则更新落入结果数据:
// 使用一个 List 来模拟最大堆,维护当前的建筑物高度
List<Integer> heights = new ArrayList<>();
heights.add(0); // 初始高度为0,表示地面
int preMax = 0; // 记录上一个时刻的最大高度
// 遍历每个坐标点
for (List<Integer> p : points) {
int x = p.get(0); // 当前的横坐标
// 高度的处理+排序 也就是 1+2
// 当前时刻的最大高度是列表中的第一个元素(因为已经按降序排序)
int curMax = heights.get(0);
// 如果当前最大高度发生变化,记录当前横坐标和新高度
// 放入结果
if (curMax != preMax) {
List<Integer> temp = new ArrayList<>();
temp.add(x);
temp.add(curMax);
results.add(temp);
preMax = curMax; // 更新最大高度
}
}
整体实现
class Solution {
public List<List<Integer>> getSkyline(int[][] buildings) {
// 存储所有的坐标点(建筑物的左边界和右边界)
List<List<Integer>> points = new ArrayList<>();
// 存储最终的天际线
List<List<Integer>> results = new ArrayList<>();
// 提取每个建筑物的左边界和右边界
for (int[] b : buildings) {
// 左边界,y 为负数表示开始
List<Integer> p1 = new ArrayList<>();
p1.add(b[0]);
p1.add(-b[2]);
points.add(p1);
// 右边界,y 为正数表示结束
List<Integer> p2 = new ArrayList<>();
p2.add(b[1]);
p2.add(b[2]);
points.add(p2);
}
// 对所有坐标点按照 x 坐标排序,x 相同则按 y 排序
Collections.sort(points, (p1, p2) -> {
int x1 = p1.get(0);
int y1 = p1.get(1);
int x2 = p2.get(0);
int y2 = p2.get(1);
if (x1 != x2) {
return x1 - x2; // x 排序
} else {
return y1 - y2; // y 排序
}
});
// 使用一个 List 来模拟最大堆,维护当前的建筑物高度
List<Integer> heights = new ArrayList<>();
heights.add(0); // 初始高度为0,表示地面
int preMax = 0; // 记录上一个时刻的最大高度
// 遍历每个坐标点
for (List<Integer> p : points) {
int x = p.get(0); // 当前的横坐标
int y = p.get(1); // 当前的纵坐标(建筑物的高度,负值表示开始,正值表示结束)
if (y < 0) {
// 左边界,表示新的建筑物开始,加入高度
heights.add(-y); // 加入负值转换后的高度
} else {
// 右边界,表示建筑物结束,从列表中移除该高度
heights.remove(Integer.valueOf(y)); // 从列表中移除该高度
}
// 每次都重新排序,确保 heights 中的最大值在最后面
Collections.sort(heights, (h1, h2) -> h2 - h1); // 按高度降序排序
// 当前时刻的最大高度是列表中的第一个元素(因为已经按降序排序)
int curMax = heights.get(0);
// 如果当前最大高度发生变化,记录当前横坐标和新高度
if (curMax != preMax) {
List<Integer> temp = new ArrayList<>();
temp.add(x);
temp.add(curMax);
results.add(temp);
preMax = curMax; // 更新最大高度
}
}
return results;
}
}
效果
1423ms
击败 5.45%
v2-排序+最大堆
思路
我们不要每一次都排序,而是使用最大堆来替代。
PriorityQueue 代替 LinkedList,避免多次排序。
实现
public List<List<Integer>> getSkyline(int[][] buildings) {
List<List<Integer>> points = new ArrayList<>();
List<List<Integer>> results = new ArrayList<>();
int n = buildings.length;
//求出左上角和右上角坐标, 左上角坐标的 y 存负数
for (int[] b : buildings) {
List<Integer> p1 = new ArrayList<>();
p1.add(b[0]);
p1.add(-b[2]);
points.add(p1);
List<Integer> p2 = new ArrayList<>();
p2.add(b[1]);
p2.add(b[2]);
points.add(p2);
}
//将所有坐标排序
Collections.sort(points, new Comparator<List<Integer>>() {
@Override
public int compare(List<Integer> p1, List<Integer> p2) {
int x1 = p1.get(0);
int y1 = p1.get(1);
int x2 = p2.get(0);
int y2 = p2.get(1);
if (x1 != x2) {
return x1 - x2;
} else {
return y1 - y2;
}
}
});
//默认的优先队列是最小堆,我们需要最大堆,每次需要得到队列中最大的元素
Queue<Integer> queue = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer i1, Integer i2) {
return i2 - i1;
}
});
queue.offer(0);
int preMax = 0;
for (List<Integer> p : points) {
int x = p.get(0);
int y = p.get(1);
//左上角坐标
if (y < 0) {
queue.offer(-y);
//右上角坐标
} else {
queue.remove(y);
}
int curMax = queue.peek();
//最大值更新了, 将当前结果加入
if (curMax != preMax) {
List<Integer> temp = new ArrayList<>();
temp.add(x);
temp.add(curMax);
results.add(temp);
preMax = curMax;
}
}
return results;
}
效果
226ms
击败 7.27%
详细注释版本
public List<List<Integer>> getSkyline(int[][] buildings) {
// 用来存储所有的坐标点 (包括建筑物的开始和结束位置)
List<List<Integer>> points = new ArrayList<>();
// 用来存储结果,最终的天际线
List<List<Integer>> results = new ArrayList<>();
// 获取建筑物的数量
int n = buildings.length;
// 遍历所有建筑物,提取每个建筑物的左右边界和高度
for (int[] b : buildings) {
List<Integer> p1 = new ArrayList<>();
p1.add(b[0]); // 添加建筑物的左边界 x 坐标
p1.add(-b[2]); // 添加建筑物的高度 y 坐标,注意此处 y 坐标取负值,表示建筑物的开始
points.add(p1); // 将左边界坐标加入到 points 列表
List<Integer> p2 = new ArrayList<>();
p2.add(b[1]); // 添加建筑物的右边界 x 坐标
p2.add(b[2]); // 添加建筑物的高度 y 坐标,表示建筑物的结束
points.add(p2); // 将右边界坐标加入到 points 列表
}
// 按照 x 坐标进行排序:
// 1. 首先按 x 坐标排序(横坐标),左边界优先
// 2. 如果 x 坐标相同,则高度较大的建筑物在前(高度的负数先排),即保证在有重叠位置时,开始的建筑物先排
Collections.sort(points, new Comparator<List<Integer>>() {
@Override
public int compare(List<Integer> p1, List<Integer> p2) {
int x1 = p1.get(0); // 获取第一个坐标点的 x 坐标
int y1 = p1.get(1); // 获取第一个坐标点的 y 坐标
int x2 = p2.get(0); // 获取第二个坐标点的 x 坐标
int y2 = p2.get(1); // 获取第二个坐标点的 y 坐标
// 如果横坐标不同,按横坐标排序
if (x1 != x2) {
return x1 - x2;
} else {
// 如果横坐标相同,按高度排序(负数表示建筑物开始,正数表示结束)
return y1 - y2;
}
}
});
// 创建一个优先队列(最大堆),用于存储建筑物的高度
// 默认的 PriorityQueue 是最小堆,这里我们需要最大堆来确保每次能够得到当前最大高度
Queue<Integer> queue = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer i1, Integer i2) {
// 为了实现最大堆,反转比较顺序
return i2 - i1;
}
});
// 初始时,将高度 0 加入队列(表示地面)
queue.offer(0);
int preMax = 0; // 记录上一个时刻的最大高度
// 遍历所有排序后的坐标点
for (List<Integer> p : points) {
int x = p.get(0); // 当前的横坐标
int y = p.get(1); // 当前的纵坐标(建筑物的高度,负值表示开始,正值表示结束)
// 如果 y 是负值,表示建筑物的左边界(开始),加入高度到队列
if (y < 0) {
queue.offer(-y); // 注意此处把负值转换回正值(即建筑物的高度)
// 如果 y 是正值,表示建筑物的右边界(结束),从队列中移除该高度
} else {
queue.remove(y); // 从队列中移除该建筑物的高度
}
// 获取当前队列中最大值(当前时刻的最大高度)
int curMax = queue.peek();
// 如果当前的最大高度发生变化,记录新的关键点
if (curMax != preMax) {
List<Integer> temp = new ArrayList<>();
temp.add(x); // 当前横坐标
temp.add(curMax); // 当前最大高度
results.add(temp); // 将关键点加入结果列表
preMax = curMax; // 更新最大高度
}
}
// 返回最终的天际线结果
return results;
}
详细解释:
-
建筑物转化为坐标点:
-
每个建筑物的左边界和右边界会分别变成一个坐标点。为了方便处理,建筑物的左边界使用负数来表示高度(
-height),右边界使用正数来表示高度。 -
例如,建筑物
[2, 9, 10]会被转化为两个坐标点:-
左边界:
[2, -10](横坐标为2,表示开始,负值表示高度) -
右边界:
[9, 10](横坐标为9,表示结束,正值表示高度)
-
-
-
排序:
- 我们需要将所有的事件(左边界和右边界)按横坐标进行排序。如果横坐标相同,优先处理高度大的建筑物,这样可以保证在同一个横坐标处,如果有多个建筑物重叠,先考虑开始的建筑物。
-
使用最大堆管理当前的建筑物高度:
-
我们使用优先队列(
PriorityQueue)来维护当前活跃的建筑物的高度。队列中的元素始终是建筑物的高度,而队列的顶部(peek())始终是当前最大高度。 -
由于 Java 默认使用最小堆,我们通过自定义比较器,使其变成最大堆,这样每次
peek()就能得到最大高度。
-
-
遍历坐标点并更新天际线:
-
每当遇到左边界时,我们将该建筑物的高度加入堆。
-
每当遇到右边界时,我们将该建筑物的高度从堆中移除。
-
每次堆中的最大高度发生变化时,记录下当前横坐标和新的最大高度作为关键点。通过记录关键点,我们就可以拼接出天际线。
-
-
返回最终结果:
- 最终的天际线由一系列的关键点组成,
results列表保存这些关键点。
- 最终的天际线由一系列的关键点组成,
为什么???
在这道天际线问题中,我们通过堆来动态地维护当前所有活跃建筑物的高度。
在建筑物的左边界和右边界处,天际线的形状可能发生变化。下面详细解释为什么要在左边界和右边界处做这些操作:
1. 遇到左边界时,将该建筑物的高度加入堆:
- 左边界表示建筑物的开始。
- 当一个建筑物的左边界被处理时,我们知道这座建筑物正在进入天际线的视野,开始对天际线的形状产生影响。
- 由于当前的建筑物可能会有比其他活跃建筑物更高的高度,因此我们需要将它的高度加入堆中。堆能够在 O(log N) 时间内保持最大值在顶部,因此我们可以快速得到当前所有建筑物的最大高度。
- 为什么要加入堆?
- 建筑物的高度决定了天际线的高度。天际线的高度会随着建筑物的开始(左边界)或结束(右边界)发生变化。如果当前建筑物比堆中的其他建筑物高,它将会影响天际线的形状,因此需要将它的高度添加到堆中。
2. 遇到右边界时,将该建筑物的高度从堆中移除:
- 右边界表示建筑物的结束。
- 当处理一个建筑物的右边界时,意味着该建筑物已经结束,它的高度对天际线的影响也结束了。因此,需要将该建筑物的高度从堆中移除。
- 由于堆是动态变化的,移除高度后,堆会重新排列,保证堆的顶部总是当前活跃建筑物中的最大高度。
- 为什么要移除堆中的高度?
- 移除该建筑物的高度是为了保证堆中的建筑物只包含当前在视野内的建筑物。对于那些已经结束的建筑物,它们不再对天际线的高度产生影响。因此,必须从堆中移除它们的高度,这样堆中的最大值(即当前天际线的高度)才是准确的。
3. 堆中的最大高度发生变化时,记录关键点:
- 关键点是天际线的转折点。
- 当堆中的最大高度发生变化时(即新的建筑物的高度比原来的最大高度更高,或者一个建筑物结束,导致当前的最大高度降低),我们就记录下一个关键点。
- 为什么要记录关键点? 关键点是天际线变化的地方,是我们要输出的天际线的点。这些点是天际线的“拐点”,在这些点之间天际线的高度会保持不变。所以,我们需要在每个关键点记录当前的横坐标(x)和天际线的高度(y)。
为什么要通过这些操作来拼接天际线?
- 天际线的形状由建筑物的开始和结束决定:
- 每当一个建筑物开始时(遇到左边界),可能会增加天际线的高度。
- 每当一个建筑物结束时(遇到右边界),可能会降低天际线的高度。
- 通过动态地维护堆中的最大高度,我们可以实时知道当前天际线的高度,并在发生变化时记录下来。
- 天际线的变化只有在高度发生变化时才有意义:
- 例如,如果多个建筑物的顶部在同一个 x 坐标上重叠(高度相同),那么在这些位置天际线的高度并没有发生变化,我们不需要记录这些点。
- 只有当天际线的高度变化时,才会有新的关键点,这些关键点标记了天际线的转折。
v3-TreeMap 实现优化
优化思路
代码的话还能优化一下,上边代码中最常出现的三种操作。
添加高度,时间复杂度 O(log(n))。
删除高度,时间复杂度 O(n)。
查看最大高度,时间复杂度 O(1)。
有一个操作是 O(n),加上外层的遍历,所以会使得最终的时间复杂度成为 O(n²) 。
之所以是上边的时间复杂度,因为我们使用的是优先队列。
我们还可以使用 TreeMap,这样上边的三种操作时间复杂度就都是 O(log(n)) 了,最终的时间复杂度就变为 O(nlog(n))
TreeMap 的话 key 当然就是存高度了,因为可能添加重复的高度,所有value 的话存高度出现的次数即可。
实现
代码的话,整体思想不需要改变,只需要改变添加高度、删除高度、查看最大高度的部分。
public List<List<Integer>> getSkyline(int[][] buildings) {
List<List<Integer>> points = new ArrayList<>();
List<List<Integer>> results = new ArrayList<>();
int n = buildings.length;
//求出将左上角和右上角坐标, 左上角坐标的 y 存负数
for (int[] b : buildings) {
List<Integer> p1 = new ArrayList<>();
p1.add(b[0]);
p1.add(-b[2]);
points.add(p1);
List<Integer> p2 = new ArrayList<>();
p2.add(b[1]);
p2.add(b[2]);
points.add(p2);
}
//将所有坐标排序
Collections.sort(points, new Comparator<List<Integer>>() {
@Override
public int compare(List<Integer> p1, List<Integer> p2) {
int x1 = p1.get(0);
int y1 = p1.get(1);
int x2 = p2.get(0);
int y2 = p2.get(1);
if (x1 != x2) {
return x1 - x2;
} else {
return y1 - y2;
}
}
});
TreeMap<Integer, Integer> treeMap = new TreeMap<>(new Comparator<Integer>() {
@Override
public int compare(Integer i1, Integer i2) {
return i2 - i1;
}
});
treeMap.put(0, 1);
int preMax = 0;
for (List<Integer> p : points) {
int x = p.get(0);
int y = p.get(1);
if (y < 0) {
Integer v = treeMap.get(-y);
if (v == null) {
treeMap.put(-y, 1);
} else {
treeMap.put(-y, v + 1);
}
} else {
Integer v = treeMap.get(y);
if (v == 1) {
treeMap.remove(y);
} else {
treeMap.put(y, v - 1);
}
}
int curMax = treeMap.firstKey();
if (curMax != preMax) {
List<Integer> temp = new ArrayList<>();
temp.add(x);
temp.add(curMax);
results.add(temp);
preMax = curMax;
}
}
return results;
}
效果
38ms
击败 43.64%
分治算法
思路
有些类似归并排序的思想,divide and conquer 。
首先考虑,如果只给一个建筑 [x, y, h],那么答案是多少?
很明显输出的解将会是 [[x, h], [y, 0]],也就是左上角和右下角坐标。
接下来考虑,如果有建筑 A B C D E,我们知道了建筑 A B C 输出的解和 D E 输出的解,那么怎么把这两组解合并,得到 A B C D E 输出的解。
合并方法采用归并排序中双指针的方法,将两个指针分别指向两组解的开头,然后进行比对。
具体的,看下边的例子。
每次选取 x 坐标较小的点,然后再根据一定规则算出高度,具体的看下边的过程。
Skyline1 = {(1, 11), (3, 13), (9, 0), (12, 7), (16, 0)}
Skyline2 = {(14, 3), (19, 18), (22, 3), (23, 13), (29, 0)}
Skyline1 存储第一组的解。
Skyline2 存储第二组的解。
Result 存储合并后的解, Result = {}
h1 表示将 Skyline1 中的某个关键点加入 Result 中时, 当前关键点的高度
h2 表示将 Skyline2 中的某个关键点加入 Result 中时, 当前关键点的高度
h1 = 0, h2 = 0
i = 0, j = 0
(1, 11), (3, 13), (9, 0), (12, 7), (16, 0)
^
i
(14, 3), (19, 18), (22, 3), (23, 13), (29, 0)
^
j
比较 (1, 11) 和 (14, 3)
比较 x 坐标, 1 < 14, 所以考虑 (1, 11)
x 取 1, 接下来更新 height
h1 = 11, height = max(h1, h2) = max(11, 0) = 11
将 (1, 11) 加入到 Result 中
Result = {(1, 11)}
i 后移, i = i + 1 = 2
(1, 11), (3, 13), (9, 0), (12, 7), (16, 0)
^
i
(14, 3), (19, 18), (22, 3), (23, 13), (29, 0)
^
j
比较 (3, 13) 和 (14, 3)
比较 x 坐标, 3 < 14, 所以考虑 (3, 13)
x 取 3, 接下来更新 height
h1 = 13, height = max(h1, h2) = max(13, 0) = 13
将 (3, 13) 加入到 Result 中
Result = {(1, 11), (3, 13)}
i 后移, i = i + 1 = 3
(9, 0) 和 (12, 7) 同理
此时 h1 = 7
Result 为 {(1, 11), (3, 13), (9, 0), (12, 7)}
i = 4
(1, 11), (3, 13), (9, 0), (12, 7), (16, 0)
^
i
(14, 3), (19, 18), (22, 3), (23, 13), (29, 0)
^
j
比较 (16, 0) 和 (14, 3)
比较 x 坐标, 14 < 16, 所以考虑 (14, 3)
x 取 14, 接下来更新 height
h2 = 3, height = max(h1, h2) = max(7, 3) = 7
将 (14, 7) 加入到 Result 中
Result = {(1, 11), (3, 13), (9, 0), (12, 7), (14, 7)}
j 后移, j = j + 1 = 2
(1, 11), (3, 13), (9, 0), (12, 7), (16, 0)
^
i
(14, 3), (19, 18), (22, 3), (23, 13), (29, 0)
^
j
比较 (16, 0) 和 (19, 18)
比较 x 坐标, 16 < 19, 所以考虑 (16, 0)
x 取 16, 接下来更新 height
h1 = 0, height = max(h1, h2) = max(0, 3) = 3
将 (16, 3) 加入到 Result 中
Result = {(1, 11), (3, 13), (9, 0), (12, 7), (14, 7), (16, 3)}
i 后移, i = i + 1 = 5
因为 Skyline1 没有更多的解了,所以只需要将 Skyline2 剩下的解按照上边 height 的更新方式继续加入到 Result 中即可
Result = {(1, 11), (3, 13), (9, 0), (12, 7), (14, 7), (16, 3),
(19, 18), (22, 3), (23, 13), (29, 0)}
我们会发现上边多了一些解, (14, 7) 并不是我们需要的, 因为之前已经有了 (12, 7), 所以我们需要将其去掉。
Result = {(1, 11), (3, 13), (9, 0), (12, 7), (16, 3), (19, 18),
(22, 3), (23, 13), (29, 0)}
实现
代码的话,模仿归并排序,我们每次将 buildings 对半分,然后进入递归,将得到的两组解按照上边的方式合并即可。
public List<List<Integer>> getSkyline(int[][] buildings) {
if(buildings.length == 0){
return new ArrayList<>();
}
return merge(buildings, 0, buildings.length - 1);
}
private List<List<Integer>> merge(int[][] buildings, int start, int end) {
List<List<Integer>> res = new ArrayList<>();
//只有一个建筑, 将 [x, h], [y, 0] 加入结果
if (start == end) {
List<Integer> temp = new ArrayList<>();
temp.add(buildings[start][0]);
temp.add(buildings[start][2]);
res.add(temp);
temp = new ArrayList<>();
temp.add(buildings[start][1]);
temp.add(00);
res.add(temp);
return res;
}
int mid = (start + end) >>> 1;
//第一组解
List<List<Integer>> Skyline1 = merge(buildings, start, mid);
//第二组解
List<List<Integer>> Skyline2 = merge(buildings, mid + 1, end);
//下边将两组解合并
int h1 = 0;
int h2 = 0;
int i = 0;
int j = 0;
while (i < Skyline1 .size() || j < Skyline2 .size()) {
long x1 = i < Skyline1 .size() ? Skyline1 .get(i).get(0) : Long.MAX_VALUE;
long x2 = j < Skyline2 .size() ? Skyline2 .get(j).get(0) : Long.MAX_VALUE;
long x = 0;
//比较两个坐标
if (x1 < x2) {
h1 = Skyline1 .get(i).get(1);
x = x1;
i++;
} else if (x1 > x2) {
h2 = Skyline2 .get(j).get(1);
x = x2;
j++;
} else {
h1 = Skyline1 .get(i).get(1);
h2 = Skyline2 .get(j).get(1);
x = x1;
i++;
j++;
}
//更新 height
int height = Math.max(h1, h2);
//重复的解不要加入
if (res.isEmpty() || height != res.get(res.size() - 1).get(1)) {
List<Integer> temp = new ArrayList<>();
temp.add((int) x);
temp.add(height);
res.add(temp);
}
}
return res;
}
上边有两个技巧需要注意,技巧只是为了让算法更简洁一些,不用也是可以的,但可能会麻烦些。
一个就是下边的部分
long x1 = i < Skyline1 .size() ? Skyline1 .get(i).get(0) : Long.MAX_VALUE;
long x2 = j < Skyline2 .size() ? Skyline2 .get(j).get(0) : Long.MAX_VALUE;
当 Skyline1 或者 Skyline2 遍历完的时候,我们给他赋值为一个很大的数,这样的话我们可以在一个 while 循环中完成我们的算法,不用再单独考虑当一个遍历完的处理。
这里需要注意的是,我们将 x1 和 x2 定义为 long,算是一个 trick,可以保证我们给 x1 或者 x2 赋的 Long.MAX_VALUE 这个值,后续不会出现 x1 == x2。因为原始数据都是 int 范围的。
当然也可以有其他的处理方式,比如当遍历完的时候,给 x1 或者 x2 赋值成负数,不过这样的话就需要更改后续的 if 判断条件,不细说了。
另外一个技巧就是下边的部分。
if (res.isEmpty() || height != res.get(res.size() - 1).get(1)) {
我们在将当前结果加入的 res 中时,判断一下当前的高度是不是 res 中最后一个的高度,可以提前防止加入重复的点。
这道题和扫描线算法的关系?
这道天际线问题(Skyline Problem)与扫描线算法有很大的关系,它是扫描线技术的一个经典应用。
我们可以将这道题理解为一个动态处理横坐标的过程,通过“扫描”所有建筑物的左右边界来获得天际线的形状。
下面详细解释这两者的关系:
扫描线算法(Sweep Line Algorithm)
扫描线算法是一种常见的解决几何问题的技术,特别是在处理二维空间中的一些问题时。
它的基本思路是:
- 我们在空间中的某一维度(通常是横坐标)上进行扫描,逐步处理每一个可能的事件。
- 每处理一个事件,我们就更新当前的状态,并记录可能的结果。
在天际线问题中,扫描线沿着 x 轴(横坐标)从最左侧到最右侧“扫过”,遇到建筑物的左边界时开始,遇到建筑物的右边界时结束,记录这些“事件”发生时的天际线变化。
天际线问题中的扫描线实现
1. 将问题分解为事件:
- 每一个建筑物都会产生两个“事件”:
- 左边界事件:建筑物的左边缘,建筑物开始影响天际线。
- 右边界事件:建筑物的右边缘,建筑物结束影响天际线。
2. 按 x 坐标排序事件:
- 我们把所有的建筑物的左边界和右边界按 x 坐标排序,处理时从左到右扫描。
- 如果有多个事件的 x 坐标相同:
- 对于左边界事件,先处理高度较高的建筑物。
- 对于右边界事件,先处理较低的建筑物。这样可以确保在同一个位置处理多个事件时,顺序不会影响结果。
3. 维护当前活跃建筑物的高度:
- 在扫描过程中,维护一个数据结构来记录当前所有“活跃”建筑物的高度。这里使用的是一个优先队列(最大堆)或者手动排序的列表,保持当前所有活跃建筑物的最大高度。
- 左边界事件:建筑物开始时,将它的高度加入当前高度集合。
- 右边界事件:建筑物结束时,将它的高度从当前高度集合中移除。
4. 记录天际线变化的关键点:
- 每次扫描到一个新的位置,如果当前的最大高度(即堆顶的高度)发生变化,就记录下当前的横坐标和新的最大高度作为天际线的关键点。
为什么叫扫描线?
- 扫描线算法模拟了一个沿着 x 轴水平“扫过”所有建筑物的过程。
- 在每一个扫描到的 x 坐标位置,天际线的高度可能会发生变化,因此我们就记录下这些变化的“关键点”。
- 通过连接这些关键点,就得到了最终的天际线。
扫描线算法的步骤(简要总结):
- 生成事件:每个建筑物的左边界和右边界都是一个事件,分别记录建筑物的 x 坐标和高度。
- 排序事件:按 x 坐标排序,如果 x 坐标相同,左边界优先,高度高的左边界优先,右边界高的优先。
- 处理事件:扫描线沿 x 轴从左到右扫描:
- 遇到左边界,添加该建筑物的高度。
- 遇到右边界,移除该建筑物的高度。
- 如果当前的最大高度发生变化,记录关键点。
- 输出结果:最终根据记录的关键点拼接出天际线。
扫描线在天际线问题中的具体应用:
在天际线问题中,扫描线帮助我们一步步处理建筑物的左边界和右边界,动态地更新当前的天际线高度。
关键是如何高效地记录和更新建筑物的高度,以及如何在每个事件发生时判断天际线的变化。
扫描线算法的优势:
-
高效性:使用堆或类似的数据结构,可以在每个事件时以对数时间复杂度更新当前天际线的最大高度,使得整体时间复杂度相对较低。
-
可扩展性:扫描线算法可以处理很多类似的几何问题,如最短路径、图的重叠区域等。
总结:
天际线问题本质上是一个典型的扫描线问题,通过对建筑物的左右边界进行扫描,并在每个扫描位置上更新当前的最大高度来获得天际线。
通过记录关键点,我们可以得到最终的天际线轮廓。
扫描线的核心思想就是“按顺序处理每个事件,动态维护当前的状态”。
开源地址
为了便于大家学习,所有实现均已开源。欢迎 fork + star~
扫描线专题
leetcode 扫描线专题 06-扫描线算法(Sweep Line Algorithm)
leetcode 扫描线专题 06-leetcode.218 the-skyline-problem 力扣.218 天际线问题
leetcode 扫描线专题 06-leetcode.252 meeting room 力扣.252 会议室
leetcode 扫描线专题 06-leetcode.253 meeting room ii 力扣.253 会议室 II
leetcode 扫描线专题 06-leetcode.1851 minimum-interval-to-include-each-query 力扣.1851 包含每个查询的最小区间
leetcode 扫描线专题 06-leetcode.223 rectangle-area 力扣.223 矩形面积
leetcode 扫描线专题 06-leetcode.391 perfect-rectangle 力扣.391 完美矩形
leetcode 扫描线专题 06-leetcode.836 rectangle-overlap 力扣.836 矩形重叠
leetcode 扫描线专题 06-leetcode.850 rectangle-area 力扣.850 矩形面积 II
参考资料
https://leetcode.cn/problems/the-skyline-problem/
