题目

给你一个数组 rectangles ，其中 rectangles[i] = [xi, yi, ai, bi] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (xi, yi) ，右上顶点是 (ai, bi) 。

如果所有矩形一起精确覆盖了某个矩形区域，则返回 true ；否则，返回 false 。

示例 1：

输入：rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
输出：true
解释：5 个矩形一起可以精确地覆盖一个矩形区域。

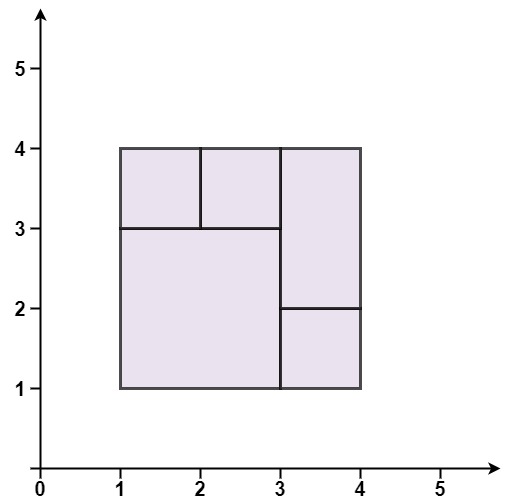
示例 2：

输入：rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
输出：false
解释：两个矩形之间有间隔，无法覆盖成一个矩形。

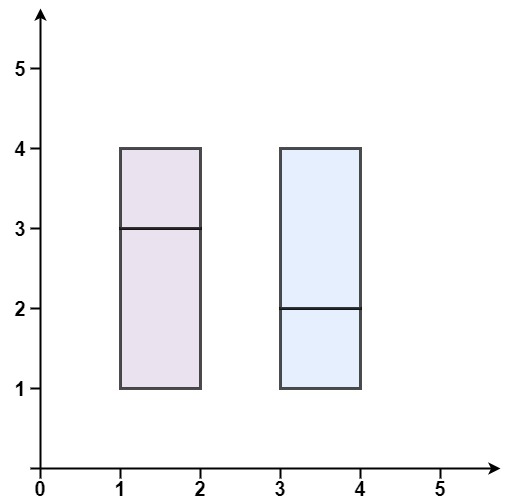
示例 3：

输入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
输出：false
解释：因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。

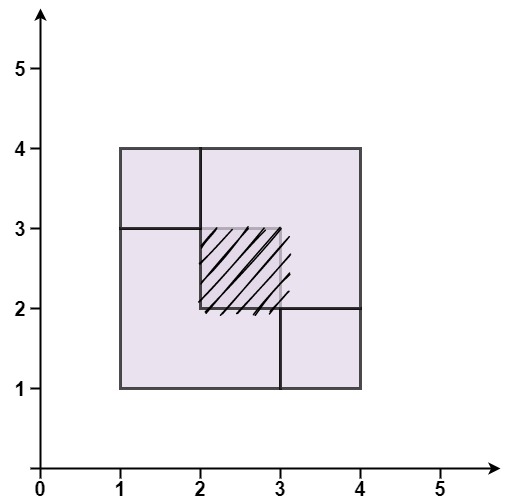
提示：

1 <= rectangles.length <= 2 * 10^4

rectangles[i].length == 4

-10^5 <= xi < ai <= 10^5

-10^5 <= yi < bi <= 10^5

v1-基本思路 HashMap

思路

完美矩形其实需要符合 2 个条件：

所有的不重合的点应该只有最后完美大矩形的 4 个顶点
小矩形的面积之和等于最后的完美大矩形的面积

我们可以用 HashMap 记录点，出现偶数次的移除。同时累加每一个小矩形的面积。

最后的 4 个点，排序一下，计算出完美矩形的面积。

代码

class Solution {
    public boolean isRectangleCover(int[][] rectangles) {
        Map<String, Integer> pointMap = new HashMap<>();

        int area = 0;
        for(int[] ints : rectangles) {
            String one = ints[0]+","+ints[1];
            String two = ints[2]+","+ints[3];
            String three = ints[0]+","+ints[3];
            String four = ints[2]+","+ints[1];

            pointMap.put(one, (pointMap.getOrDefault(one, 0) + 1) % 2);
            pointMap.put(two, (pointMap.getOrDefault(two, 0) + 1) % 2);
            pointMap.put(three, (pointMap.getOrDefault(three, 0) + 1) % 2);
            pointMap.put(four, (pointMap.getOrDefault(four, 0) + 1) % 2);

            int currentArea = (ints[2]-ints[0]) * (ints[3] - ints[1]);
            area += currentArea;
        }

        List<Integer> xList = new ArrayList<>();
        List<Integer> yList = new ArrayList<>();

        for(Map.Entry<String,Integer> entry : pointMap.entrySet()) {
            String key = entry.getKey();
            Integer count = entry.getValue();
            if(count == 1) {
                String[] splits = key.split(",");
                int x = Integer.parseInt(splits[0]);
                int y = Integer.parseInt(splits[1]);

                xList.add(x);
                yList.add(y);
            }
        }

        // 应该有4个点
        if(xList.size() != 4 || yList.size() != 4) {
            return false;
        }

        // 面积计算
        Collections.sort(xList);
        Collections.sort(yList);
        int fourPointArea = (xList.get(3) - xList.get(0)) * (yList.get(3) - yList.get(0));

        if(fourPointArea == area) {
            return true;
        }
        return false;
    }
}

效果

57ms 击败36.84%

小结

这种解法其实要求对题目的理解比较深入，属于【特定解法】。

v2-Set 优化

思路

这种通过 Map 计算次数的，其实也可以通过 Set 优化一下。

1）如果点不存在，则加入

2）如果存在，则移除

整体思想类似。

还有一个改良点，使我们可以在遍历所有的点的时候，直接把 4 个顶点确认出来。

也就是 (min_x,min_y) 和 (max_x, max_y) 对应最后的完美节点的左下/右上，从而直接确定面积。

实现

    public boolean isRectangleCover(int[][] rectangles) {
        // 定义事件列表
        int totalArea = 0;
        int minX = Integer.MAX_VALUE, minY = Integer.MAX_VALUE, maxX = Integer.MIN_VALUE, maxY = Integer.MIN_VALUE;

        // 顶点集合
        Set<String> points = new HashSet<>();

        for (int[] rect : rectangles) {
            int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];

            // 更新边界
            minX = Math.min(minX, x1);
            minY = Math.min(minY, y1);
            maxX = Math.max(maxX, x2);
            maxY = Math.max(maxY, y2);

            // 累加面积
            totalArea += (x2 - x1) * (y2 - y1);

            // 更新顶点集合
            String[] corners = {
                    x1 + "," + y1, x1 + "," + y2, x2 + "," + y1, x2 + "," + y2
            };
            for (String corner : corners) {
                if (!points.add(corner)) {
                    points.remove(corner);
                }
            }
        }

        // 顶点检查：精确覆盖的矩形应该只有 4 个顶点
        if (points.size() != 4 ||
                !points.contains(minX + "," + minY) ||
                !points.contains(minX + "," + maxY) ||
                !points.contains(maxX + "," + minY) ||
                !points.contains(maxX + "," + maxY)) {
            return false;
        }

        // 检查总面积是否一致
        int expectedArea = (maxX - minX) * (maxY - minY);
        return expectedArea == totalArea;
    }

效果

39ms 击败 68.42%

效果好好一点。

v3-扫描线

思路

做算法，还是要看三叶！

【宫水三叶】常规扫描线题目

将每个矩形 rectangles[i] 看做两条竖直方向的边，使用 (x,y1,y2) 的形式进行存储（其中 y1 代表该竖边的下端点，y2 代表竖边的上端点），同时为了区分是矩形的左边还是右边，再引入一个标识位，即以四元组 (x,y1,y2,flag) 的形式进行存储。

一个完美矩形的充要条件为：对于完美矩形的每一条非边缘的竖边，都「成对」出现（存在两条完全相同的左边和右边重叠在一起）；对于完美矩形的两条边缘竖边，均独立为一条连续的（不重叠）的竖边。

如图（红色框的为「完美矩形的边缘竖边」，绿框的为「完美矩形的非边缘竖边」）：

扫描线

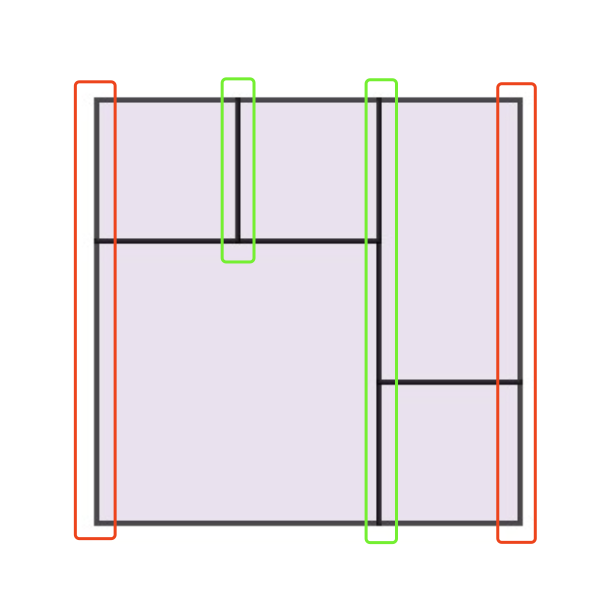
绿色：非边缘竖边必然有成对的左右两条完全相同的竖边重叠在一起；

红色：边缘竖边由于只有单边，必然不重叠，且连接成一条完成的竖边。

实现

class Solution {
    public boolean isRectangleCover(int[][] rectangles) {
        int len = rectangles.length*2, ids = 0;
        int[][] re = new int [len][4];
        //初始化re数组,组成[横坐标,纵坐标下顶点,纵坐标上顶点,矩形的左边or右边标志]
        for(int[] i:rectangles){
            re[ids++] = new int[]{i[0],i[1],i[3],1};
            re[ids++] = new int[]{i[2],i[1],i[3],-1};
        }
        //排序,按照横坐标进行排序,横坐标相等就按纵坐标排序
        Arrays.sort(re,(o1,o2)-> o1[0]!=o2[0]?o1[0]-o2[0]:o1[1]-o2[1]);

        //操作每一个顶点，判断是否符合要求
        for(int i = 0; i < len;){
            //如果该边是矩形的左边界,就加入left
            List<int[]> left = new ArrayList<>();
            //如果该边是矩形的左边界,就加入right
            List<int[]> right = new ArrayList<>();
            //标志该边是不是 矩形的左边
            boolean flag = i == 0;
            //判断横坐标相同情况下的边
            int x = i;
            while(x<len&&re[x][0]==re[i][0]) x++;
            //判断该横坐标的 边是不是符合要求
            while(i<x){
                //因为是引用数据类型,所以可以直接操作list,相当于操作left或者right
                List<int[]> list = re[i][3]==1?left:right;
                if(list.isEmpty()){
                    list.add(re[i++]);
                }else{
                    int[] pre = list.get(list.size()-1);
                    int[] cur = re[i++];
                    //有重叠 直接放回false
                    if(cur[1]<pre[2]) return false;
                    if(cur[1]==pre[2]) pre[2] = cur[2];
                    else list.add(cur);
                }
            }
            //判断边是中间边还是边界边
            if(!flag&&x<len){
                //如果是中间边 判断左右是不是相等
                if(left.size()!=right.size()) return false;
                for(int j = 0; j < left.size(); ++j){
                    if(left.get(j)[2]==right.get(j)[2]&&left.get(j)[1]==right.get(j)[1]) continue;
                    return false;
                }
            } else {
                //如果是边界边判断是不是一条
                if (left.size()!=1&&right.size()==0||left.size()==0&&right.size()!=1) return false;
            }
        }
        return true;
    }
}